Алгоритм Витерби, нетвердый код для общего случая Java

Question

Моя задача - найти наиболее вероятные последовательности слов в предложении, используя алгоритм Витерби. Данная последовательность состояний здесь: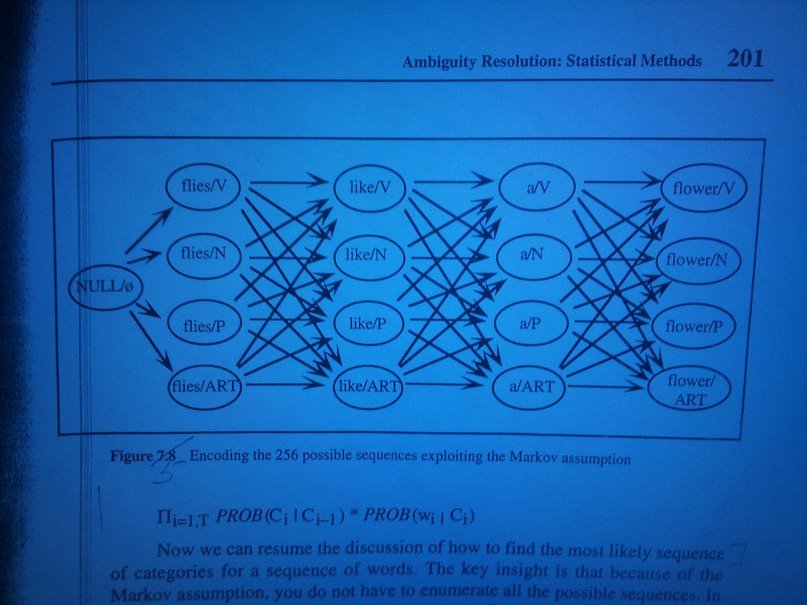Я должен ввести начальные вероятности и переходные вероятности, а затем вывести наиболее вероятную последовательность частей речи, из которой состоят слова предложения. Результат должен быть чем-то вроде N P V ART, вероятность 0,0000123 Я жестко запрограммировал его на Java, но есть ли общий случай или уже подготовленные решения в разных программах MATH? спасибо, вот что у меня так далеко:

import java.util.Hashtable;

public class Main
{
    //We hard-code start states and consequent observations.
        static final String NOUN = "Noun";
        static final String ARTICLE = "Article";

        static final String VERB = "Verb";
        static final String ADJECTIVE = "Adjective";
        static final String ADVERB = "Adverb";

        public static void main(String[] args)
        {
//We put them in array
                String[] states = new String[] {NOUN, ARTICLE};

                String[] observations = new String[] {VERB, ADJECTIVE, ADVERB};

        //Define a hashtable where we’ll keep initial states and their probabilities
                Hashtable<String, Float> start_probability = new Hashtable<String, Float>();
                start_probability.put(NOUN, 0.6f);
                start_probability.put(ARTICLE, 0.4f);

                // A hashtable with transition_probabilities which contains initial probablilities
                Hashtable<String, Hashtable<String, Float>> transition_probability =
                        new Hashtable<String, Hashtable<String, Float>>();
                        Hashtable<String, Float> t1 = new Hashtable<String, Float>();
                        t1.put(NOUN, 0.7f);
                        t1.put(ARTICLE, 0.3f);
                        Hashtable<String, Float> t2 = new Hashtable<String, Float>();
                        t2.put(NOUN, 0.4f);
                        t2.put(ARTICLE, 0.6f);
                transition_probability.put(NOUN, t1);
                transition_probability.put(ARTICLE, t2);


                //  Here we put  hashtables with consequent observed emission_probability
                Hashtable<String, Hashtable<String, Float>> emission_probability =
                        new Hashtable<String, Hashtable<String, Float>>();
                        Hashtable<String, Float> e1 = new Hashtable<String, Float>();
                        e1.put(VERB, 0.1f);
                        e1.put(ADJECTIVE, 0.4f);
                        e1.put(ADVERB, 0.5f);
                        Hashtable<String, Float> e2 = new Hashtable<String, Float>();
                        e2.put(VERB, 0.6f);
                        e2.put(ADJECTIVE, 0.3f);
                        e2.put(ADVERB, 0.1f);
                emission_probability.put(NOUN, e1);
                emission_probability.put(ARTICLE, e2);

    //We return the most probabilistic sequence with function forward fiterb described below
                Object[] ret = forward_viterbi(observations,
                           states,
                           start_probability,
                           transition_probability,
                           emission_probability);
                System.out.println(((Float) ret[0]).floatValue());
                System.out.println((String) ret[1]);
                System.out.println(((Float) ret[2]).floatValue());
        }
//Function to go
//As argument we get nested hashtables
        public static Object[] forward_viterbi(String[] obs, String[] states,
                        Hashtable<String, Float> start_p,
                        Hashtable<String, Hashtable<String, Float>> trans_p,
                        Hashtable<String, Hashtable<String, Float>> emit_p)
        {
                Hashtable<String, Object[]> T = new Hashtable<String, Object[]>();
                for (String state : states)
                        T.put(state, new Object[] {start_p.get(state), state, start_p.get(state)});

                for (String output : obs)
                {
                        Hashtable<String, Object[]> U = new Hashtable<String, Object[]>();
                        for (String next_state : states)
                        {
                                float total = 0;
                                String argmax = "";
                                float valmax = 0;

                                float prob = 1;
                                String v_path = "";
                                float v_prob = 1;

                                for (String source_state : states)
                                {
                                        Object[] objs = T.get(source_state);
                                        prob = ((Float) objs[0]).floatValue();
                                        v_path = (String) objs[1];
                                        v_prob = ((Float) objs[2]).floatValue();

                                        float p = emit_p.get(source_state).get(output) *
                                                          trans_p.get(source_state).get(next_state);
                                        prob *= p;
                                        v_prob *= p;
                                        total += prob;
                                        if (v_prob > valmax)
                                        {
                                                argmax = v_path + "," + next_state;
                                                valmax = v_prob;
                                        }
                                }
                                U.put(next_state, new Object[] {total, argmax, valmax});
                        }
                        T = U;
                }

                float total = 0;
                String argmax = "";
                float valmax = 0;

                float prob;
                String v_path;
                float v_prob;

                for (String state : states)
                {
                        Object[] objs = T.get(state);
                        prob = ((Float) objs[0]).floatValue();
                        v_path = (String) objs[1];
                        v_prob = ((Float) objs[2]).floatValue();
                        total += prob;
                        if (v_prob > valmax)
                        {
                                argmax = v_path;
                                valmax = v_prob;
                        }
                }
                return new Object[]{
                        total, argmax, valmax


                        };
                }
}