Биг-о Фибоначчи с памяткой?
Когда я запустил эту программу, мне показалось, что это O(1), потому что она была почти для больших чисел для выдумки без запоминания. Если он вычисляет предыдущие числа, то все, что он должен сделать, это добавить, и у него будет результат, который будет O(1)?
memo = {}
def Fib(n):
if (n < 2):
return 1
if not n in memo:
memo[n] = Fib(n-1) + Fib(n-2)
return memo[n]
Я также рассчитал время по сравнению с программой Фибоначчи без запоминания, и вот результат графика от 1 до 40: 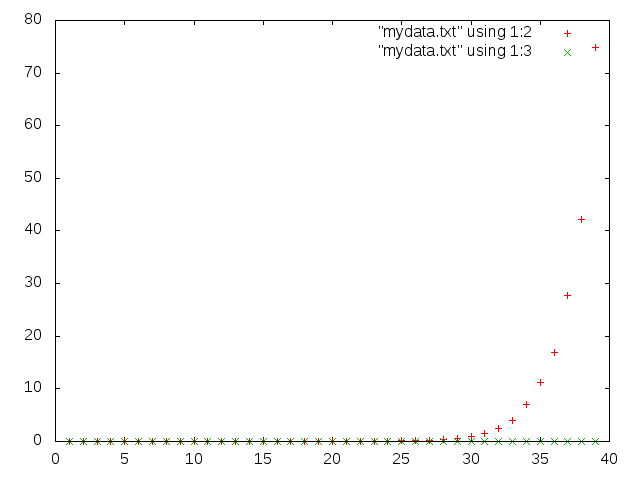
2 ответа
Прежде всего, нижняя граница вашего алгоритма O(n) просто потому что для данного n Вы заполняете словарь n значения (это предполагает, что мы имеем дело с первым вызовом Fib).
С другой стороны, для каждого n каждая операция, которую вы делаете внутри Fib функция O(1) амортизируется. В общем, вы получите первый звонок Fib является O(n) амортизируется.
Обратите внимание, что для огромных n это может пойти выше O(n) так как not in операция не O(1) (это только O(1) амортизируется). Как огромный n должен быть? Не знаю, зависит от основной функции хеширования. Кроме того, вам может не хватить памяти, прежде чем вы достигнете такого n,
Теперь это очевидно за счет пространства (то есть памяти), который становится O(n) также. И это только в предположении, что каждое целое число занимает одинаковое количество места, что, к сожалению, неверно для Python. Следствием подхода "без ограничений для целых чисел" является то, что большие целые числа хранятся в памяти в виде массива цифр. Так как ряд n имеет максимум log_b(n)+1 цифры (где b это числовая система, например 10 для десятичной системы, я не уверен, какой Python использует внутренне) мы получаем, что реальная сложность пространства где-то между O(n) а также O(log_b(n!)),
Все усложняется, если нам все равно, первый это звонок или нет. Но только немного. Вы можете легко проверить это вообще Fib является O(max(n-k, 1)) сложность, где k это размер memo словарь на момент звонка.
Сравните это, например, с итерационным методом. В этом методе вы всегда сохраняете 2 последних элемента и счетчик. Таким образом, вы получаете O(n) сложность времени и O(1) космическая сложность.
Конечно, для наивного рекурсивного Фибоначчи сложность времени O(2^n) с O(n) сложность пространства (из-за стека вызовов).
Я чувствую, что это все еще O(n), скажем, вы вычислили Fin(100), вам нужно будет вычислить все числа, прежде чем получить 100. Конечно, если предыдущий прогон был сделан, то у вас будет это в памяти, но для любого числа, которое вы можете себе представить и выполнившего предыдущее исполнение, я могу представить большее:)
Возможно, вы могли бы сказать, что это O(1) амортизируется (так же, как это O(1) для ArrayList в Java, чтобы получить элемент... в действительности это O(n), так как вам может потребоваться изменить размер массива, но обычно это не так, поэтому O(1) является "приемлемой" мерой).