как нарисовать асимптоту пунктирной линией?

Question

Я бы хотел, чтобы асимптота функции tg(x) была нарисована пунктирной линией, но я не знаю, как изменить ее в этом коде:

import matplotlib.ticker as tck
import matplotlib.pyplot as plt
import numpy as np
f,ax=plt.subplots(figsize=(8,5))
x=np.linspace(-np.pi, np.pi,100)
y=np.sin(x)/np.cos(x)
plt.ylim([-4, 4])
plt.title("f(x) = tg(x)")
plt.xlabel("x")
plt.ylabel("y")
ax.plot(x/np.pi,y)
ax.xaxis.set_major_formatter(tck.FormatStrFormatter('%g $\pi$'))

Answer 1

Интересный вопрос. Мой подход заключается в поиске разрывов путем изучения производной функции и разделения исходной функции на основе местоположения этих разрывов.

Таким образом, для tan(x), поскольку производная всегда положительна (вне асимптот), ищем точки, в которых np.diff(y) < 0. На основе всех мест, где выполняется предыдущее условие, мы разбиваем исходную функцию на сегменты и строим их по отдельности (с одинаковыми свойствами графика, чтобы линии выглядели одинаково), а затем отдельно чертим пунктирные линии. Следующий код показывает, как это работает:

import matplotlib.ticker as tck
import matplotlib.pyplot as plt
import numpy as np
f,ax=plt.subplots(figsize=(8,5))
x=np.linspace(-np.pi, np.pi,100)
y=np.sin(x)/np.cos(x)
plt.ylim([-4, 4])
plt.title("f(x) = tg(x)")
plt.xlabel("x")
plt.ylabel("y")
ax.xaxis.set_major_formatter(tck.FormatStrFormatter('%g $\pi$'))

# Search for points with negative slope
dydx = np.diff(y)
negativeSlopeIdx = np.nonzero(dydx < 0)[0]

# Take those points and parse the original function into segments to plot
yasymptote = np.array([-4, 4])
iprev = 0
for i in negativeSlopeIdx:
    ax.plot(x[iprev:i-1]/np.pi, y[iprev:i-1], "b", linewidth=2)
    ax.plot(np.array([x[i], x[i]])/np.pi, yasymptote, "--k")
    iprev = i+1


ax.plot(x[iprev:]/np.pi, y[iprev:], "b", linewidth=2)
plt.show()

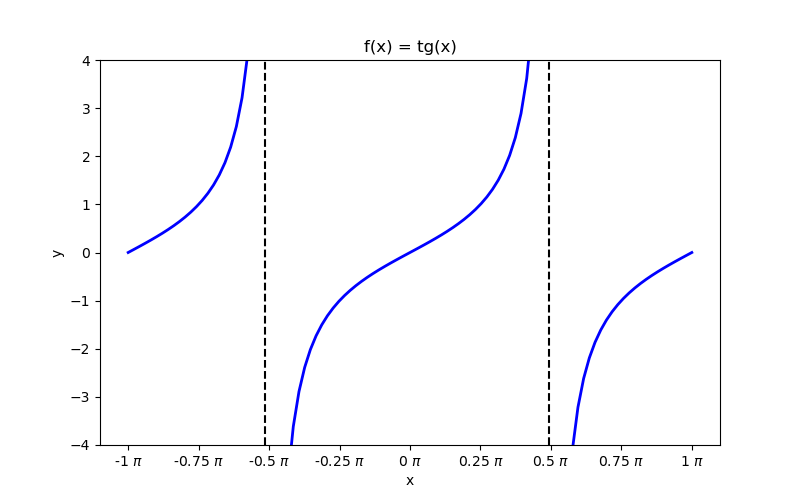
Окончательный сюжет выглядит так: