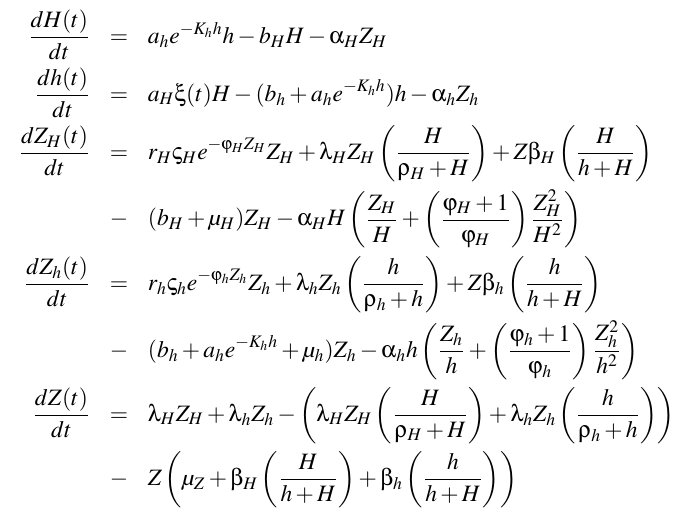Как найти неподвижные точки или найти неподвижные точки (численно) в этой системе с помощью Matlab?
Надеюсь помочь мне в этой проблеме. Мне нравится находить точки исправления в этой системе.
Я написал код в Matlab следующим образом:
clear all;
close all;
clc;
%
tic;
rand('state',sum(100*clock)); % seed
%
numreps=2; % Number of iterations
for j=1:numreps
options = odeset('RelTol',1e-6,'Stats','on');
% Parameters values of adults and tadpoles
% Fecundity (number of new individuals)
aH = 800; % minimum number offsprings
% per each host adults per year
% Mitchell 2008
% Metamorphosis rate
ah = 0.16; % Metamorphosis rate per year
% Mitchell 2008
% Natural dead hosts whitout infection
bH = 0.73; % Natural mortality rate in adults
% per year Mitchell 2008
bh = 7.55; % Natural mortality rate in adults
% per year Mitchell 2008
% Host mortality due to infection
alphaH = 0.001; % Mortality rate per adult host
% per unit time due to infection
% this work
alphah = 3.25; % Mortality rate per adult host
% per unit time due to infection
% this work
% Natural mortality zoospores within hosts
muH = 117*52; % Natural mortality in zoospores
% in adults Woodhams 2008 at an
% average temperature 17.38 per year
muh = 117*52; % Natural mortality in zoospores
% in adults Woodhams 2008 at an
% average temperature 17.38 per year
%zoospore release rate
lambdaH = 1*10^5; % Release rate of new zoospores
% within the body of the tadpole
% host to the pool per year Mitchel 2008
lambdah = 6.6*10^5; % Release rate of new zoospores
% within the body of the tadpole
% host to the pool per year Mitchel 2008
% Zoospores recruitment rate within host
rH = 124*52; % Maximum birth rate of new zoospores
% within the pre-adult host body
% per unit time Woodhams et al 2008
rh = 124*52; % Maximum birth rate of new zoospores
% within the pre-adult host body
% per unit time Woodhams et al 2008
% Zoospores transmission rate since pool
% Mitchell 2008
betaH = 6*10^-9; % Rate of transmission of a spore
% to an individual per year
% Mitchell pre-adult 2008
betah = 6*10^-9; % Rate of transmission of a spore
% to an individual per year
% Mitchell pre-adult 2008
% Recapture factor of spores that are released by
% sporangium from the skin of the hosts
varrhoH1 = 10^-2;
varrhoH = varrhoH1*lambdaH; % Proportion of zoospores
% that are immediately absorbed into
% the skin of adult hopederos,
% who depend on the zoospores released
% by sporangiumos sporangios
varrhoh1 = 10^-2;
varrhoh = varrhoh1*lambdah; % Proportion of zoospores
% that are immediately absorbed into
% the skin of adult hopederos,
% who depend on the zoospores released
% by sporangiumos sporangios
% Maximum absorption factor of
% zoospores by host values taken
% from Woodhams 2008
phiH = 10^4; % Inverse absorption factor
% per host, if low
% absorption is high and viceversa
phih = 10^4; % Inverse absorption factor
% per host, if low
% absorption is high and viceversa
% Natural mortality of zoospores into the pool
muZ = 45*52; % Tasa de mortalidad natural
% de la zoosporas Castro 2015
% por año
% Carrying capacity of species
KH = 10^5; % adults host
Kh = 10^5; % tadpoles host
%x(1) = H; x(2) = h; x(3) = ZH;
%x(4) = Zh; x(5) = Z;
G = @(t, x, ah, aH, bh, bH, muh, muH, alphah, ...
alphaH, lambdah, lambdaH, rh, rH, phih, phiH, ...
varrhoh, varrhoH, muZ, betaH, betah, Kh, KH) ...
[ah * x(2) * exp(-Kh * x(2)) - bH * x(1) - alphaH * x(3); ...
aH * x(1) - (bh + ah * exp(-Kh * x(2))) * x(2) - alphah * x(4); ...
rH * x(3) * exp(-phiH * x(3)) + lambdaH * x(3) * (x(1)./(varrhoH + x(1))) + x(5) * betaH * (x(1)./(x(1) + x(2))) - x(3) * (bH + muH) - alphaH * x(1) * (x(3)./x(1) + (x(3)./x(1))^2 * ((phiH + 1)./phiH)); ...
rh * x(4) * exp(-phih * x(4)) + lambdah * x(4) * (x(2)./(varrhoh + x(2))) + x(5) * betah * (x(2)./(x(1) + x(2))) - x(4) * (bh + ah * exp(-Kh * x(2)) + muh) - alphah * x(2) * (x(4)./x(2) + (x(4)./x(2))^2 * ((phih + 1)./phih)); ...
lambdaH * x(3) + lambdah * x(4) - x(5) * (muZ + betaH * (x(1)./(x(1) + x(2))) + betah * (x(2)./(x(1) + x(2))))-(lambdaH * x(3) * (x(1)./(varrhoH + x(1))) + lambdah * x(4) * (x(2)./(varrhoh + x(2))))];
%tspan = [0:0.001:50];
x0 = [100 100 10 10 500];
[t,xa] = ode45(@(t,x) G(t, x, ah, aH, bh, bH, muh, muH, ...
alphah, alphaH, lambdah, lambdaH, rh, rH, phih, phiH, ...
varrhoh, varrhoH, muZ, betaH, betah, Kh, KH), ...
[0 50], x0, options);
H = xa(:,1)';
h = xa(:,2)';
Zh = xa(:,3)';
ZH = xa(:,4)';
Z = xa(:,5)';
end
Решения системы выше, когда я создаю график с помощью этого кода:
%
figure1 = figure;
% Create axes
axes1 = axes('Parent',figure1);
hold(axes1,'on');
% Create multiple lines using matrix input to plot
plot1 = plot(t,xa,'LineWidth',3,'Parent',axes1);
set(plot1(1),'DisplayName','Adults host, H(t)');
set(plot1(2),'DisplayName','Tadpoles host, h(t)');
set(plot1(3),'DisplayName','Spores into the adults, ZH(t)','LineStyle','--');
set(plot1(4),'DisplayName','Spores into the tadpole, Zh(t)','LineStyle',':');
set(plot1(5),'DisplayName','External Pool of spores, Z(t)',...
'LineStyle','-.');
% Uncomment the following line to preserve the X-limits of the axes
% xlim(axes1,[0 5]);
% Uncomment the following line to preserve the Y-limits of the axes
% ylim(axes1,[-500 3000]);
box(axes1,'on');
grid(axes1,'on');
% Create xlabel
xlabel('Time in years');
% Create ylabel
ylabel('Population size');
% Set the remaining axes properties
set(axes1,'FontSize',12);
% Create legend
legend1 = legend(axes1,'show');
set(legend1,'FontSize',10);
%}
и это график
согласно предыдущему графику решения системы сходятся к неподвижным точкам. Есть ли способ численно рассчитать фиксированные точки предыдущей системы с помощью Matlab?