Площадь между кривыми с произвольным числом пересечений в MATLAB

Question

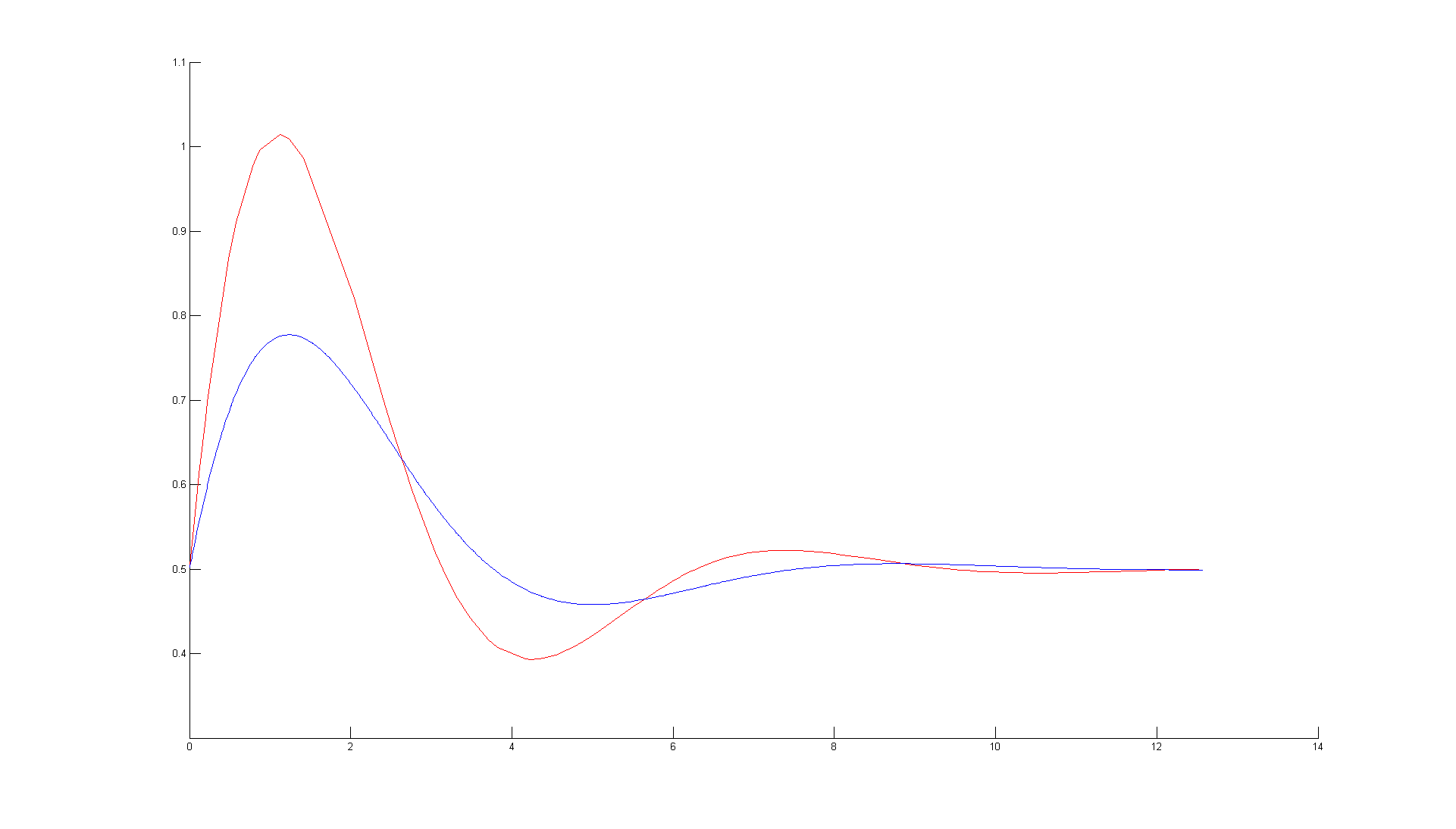
Я ищу, чтобы вычислить площадь между двумя кривыми в Matlab, которые имеют разные диапазоны х. Есть два случая. Я хочу, чтобы область была положительной, когда одна кривая (красная на графике) выше другой, и отрицательной, когда эта кривая находится ниже синей кривой. Я понимаю, что это, как правило, простая проблема, и обычно можно найти все точки пересечения между двумя кривыми, но в моем случае количество пересечений может быть довольно большим. Моя трудность заключается в том, что в зависимости от рассматриваемого набора данных две кривые будут пересекаться любое количество раз или не пересекаться вообще.

Пример:

n=4
x = n*pi*rand(100,1);
x=[0;x;pi];
x=sort(x);
y=.5+exp(-.5*x).*sin(x);
x2 = n*pi*rand(1000,1);
x2=[0;x2;pi];
x2=sort(x2);
y2=.5+exp(-.5*x2).*0.6.*sin(x2/1.2);

figure,hold on 
plot(x,y,'r-')
plot(x2,y2,'b-')

Area1  = trapz(x, y);
Area2  = trapz(x2, y2);

Какие-либо предложения ?

Answer 1

Ваш подход для расчета площади между перекрестками является разумным. Вы можете использовать эту библиотеку для расчета точек пересечения. Прямая ссылка на ZIP-файл.

Предполагая, что у вас есть пересечения, вы можете пройти через это, чтобы вычесть область между двумя интервалами, используя trapz функция. Единственная сложная часть остается с признаком площади, если кривая 1 выше кривой 2. Для этого вы можете иметь порог epsilon и рассчитать y1 а также y2 в x2 - epsilon где (x1, x2) были X точки пересечения. y1 > y2 будет означать, что вы должны сделать Area 1 - Area2,

С учетом всего вышесказанного код будет выглядеть следующим образом:

%Find all intersections
[xIntersect,yIntersect] = intersections(x,y,x2,y2,1);
%Number of intersections
numIntersections = size(xIntersect, 1);
%Threshold to calculate sign of area
epsilon = 0.1;

curveArea = 0; %Initial value
lastX1Index = 1; % End X1 Index processes in last iteration
lastX2Index = 1; % End X2 Index processes in last iteration

%Loop over intersections processing pair of points hence until
%numIntersections - 1
for i = 1:numIntersections-1
%     startX = xIntersect(i); %Start of interval 
%     startY = yIntersect(i); 
    endX = xIntersect(i+1); % Next Intersection point
%     endY = yIntersect(i+1);
    xMinus = endX - epsilon; % get a X value before intersection

    %Sign of area is positive if y1Minus > y2Minus
    y1Minus = .5+exp(-.5*xMinus).*sin(xMinus); %Convert this to function1
    y2Minus = .5+exp(-.5*xMinus).*0.6.*sin(xMinus/1.2); %Convert this to function 2

    x1Index = find(x < xIntersect(i+1), 1, 'last' ); % Find last X1 element before intersection
    x2Index = find(x2 < xIntersect(i+1), 1, 'last' ); % Find last X2 element before intersection

    %Calculate area for interval
    Area1 = trapz(x(lastX1Index:x1Index), y(lastX1Index:x1Index));
    Area2 = trapz(x2(lastX2Index:x2Index), y2(lastX2Index:x2Index));

    %Store last X1, X2 Index for next run
    lastX1Index = x1Index+1;
    lastX2Index = x2Index+1;

    %Save curveArea
    if y1Minus > y2Minus
        curveArea = curveArea + (Area1 - Area2);
    else
        curveArea = curveArea + (Area2 - Area1);
    end
end

fprintf('curveArea= %f \n',curveArea);