Поверхность графика вместо параметрической кривой

Question

Я работаю над использованием прямой разностной схемы для численного решения диффузионной функции в одном измерении. Мой окончательный график решения должен быть поверхностью, где решение u(x,t) нанесено на сетку значений x и t. У меня проблема решена, но я не могу получить данные, которые будут отображены в виде сетки.

Я могу придумать 2 способа это исправить:

1.) Мои массивы x и t должны быть одномерными, но мой массив u должен быть двумерным. В конечном счете, я хочу получить квадратную матрицу для вас, но мне трудно это кодировать. В настоящее время у меня есть 1D массив для вас. Вот код, где вы заполняете.

u   = zeros(Nx+1)           # unknown u at new time level
u_1 = zeros(Nx+1)           # u at the previous time level
# Set initial condition u(x,0) = I(x)
for i in range(0, Nx+1):
#set initial u's to I(xi)
    u_1[i] = 25-x[i]**2
for n in range(0, Nt):
# Compute u at inner mesh points
    for i in range(1, Nx):
        u[i] = u_1[i] + F*(u_1[i-1] - 2*u_1[i] + u_1[i+1])

2.) Приведенный выше код возвращает одномерный массив для u, есть ли способ построить трехмерную поверхность с 3 одномерными массивами для x,y,z?

Answer 1

Ну, есть много информации, которую вы не предоставили. Например, вы сказали, что хотите построить график a x,y,z, но не сказали, какими должны быть x, y и z в контексте вашего графика. Также z обычно является z(x,y).

Следующий рецепт предполагает t а также x, а также u(t,x) в качестве переменных, которые будут помещены в поверхность. Я думаю, это не совсем ваша идея, но она должна быть адаптирована к вашим упражнениям:

РЕДАКТИРОВАТЬ: Также ваш код (который находится в функции computeU в этом рецепте) была петля для Nt кажется, ничего не делает. Я удалил его для целей этого примера.

from mpl_toolkits.mplot3d import Axes3D
from matplotlib import cm
import matplotlib.pyplot as plt
import numpy as np

def computeU(Nx,x,F,Nt):
    u   = np.zeros(Nx+1)           # unknown u at new time level
    u_1 = np.zeros(Nx+1)           # u at the previous time level
    # Set initial condition u(x,0) = I(x)
    for i in range(0, Nx+1):
    #set initial u's to I(xi)
        u_1[i] = 25-x[i]**2
    #for n in range(0, Nt): # I'm not sure what this is doing. It has no effect.
    # Compute u at inner mesh points
    for i in range(1, Nx):
        u[i] = u_1[i] + F*(u_1[i-1] - 2*u_1[i] + u_1[i+1])
    return np.hstack((u[:,np.newaxis],u_1[:,np.newaxis]))

Nx = 10
F  = 3
Nt = 5
x  = np.arange(11)
t  = np.arange(2)

X,Y = np.meshgrid(t,x)
Z = computeU(Nx,x,F,Nt)
fig = plt.figure()
ax = fig.gca(projection='3d')
surf = ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap=cm.coolwarm,linewidth=0, antialiased=False)
plt.show()

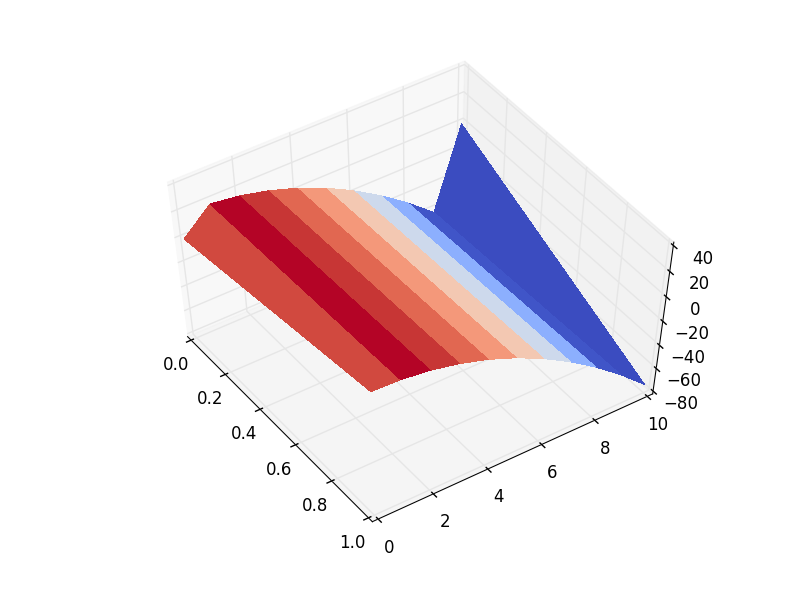
Обратите внимание, как я использовал meshgrid строить новые t,x (из 1D-массивов) для сопоставления с вашим стеком U массивы (которые будут иметь одинаковую форму X,Y - новый t,x). Результат таков: