Показать np-полноту непересекающегося гамильтонова пути

Question

Рассмотрим проблему непересекающегося гамильтонова пути:

Вход: график, который может быть направленным или ненаправленным

Вывод: существует ли в этом графе хотя бы 2 гамильтоновых пути, которые не пересекаются по ребрам? Непересекающиеся края означают, что ни один край не является общим для двух путей.

Покажите, что непересекающийся гамильтонов путь является np-полным.

Мне сказали, что эта проблема является np-полной, но я не смог доказать, что это np-сложная. Я попытался свести исходный гамильтонов путь и гамильтонов цикл к этой проблеме, но я не мог придумать решение.

Answer 1

Я пришел к следующему сокращению, не уверен, что это самое простое, но это просто.

Предположим, что G - неориентированный граф, соответствующий экземпляру HP. Теперь построим новый граф G'следующим образом:

• Держите каждую вершину из G.
• Для каждого ребра (u,v) в G создайте 4 дополнительные вершины и соедините их следующим образом:

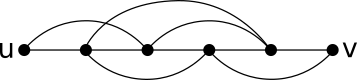
Теперь легко видеть, что если G имеет гамильтоновый путь, G'будет иметь два непересекающихся по ребру гамильтоновых пути, потому что каждое ребро было заменено некоторым подграфом, который сам имеет два непересекающихся по ребру гамильтоновых пути (идите прямо или возьмите соблазнительные ребра). И если у G'есть HP, то и у G так же, потому что как только вы введете подграф, соответствующий одному из исходных ребер, у вас не останется иного выбора, кроме как выбраться из него на другом конце, что соответствует взятию исходного ребра в G. Единственная "проблема", которая может возникнуть, - это если бы путь начинался или заканчивался внутри одного из этих подграфов, но тогда мы можем просто игнорировать небольшую часть пути, которая находится внутри, и при этом получить HP для G.

И обратите внимание, что G'имеет HP => G имеет HP => G' имеет два непересекающихся по краям HP. Таким образом, G имеет HP <=> G'имеет два непересекающихся HP края.

Преобразование, очевидно, может быть сделано за многократное время, поэтому ваша задача - NP-Hard.

Направленный случай похож, просто направьте ребра в преобразованном графе соответственно.