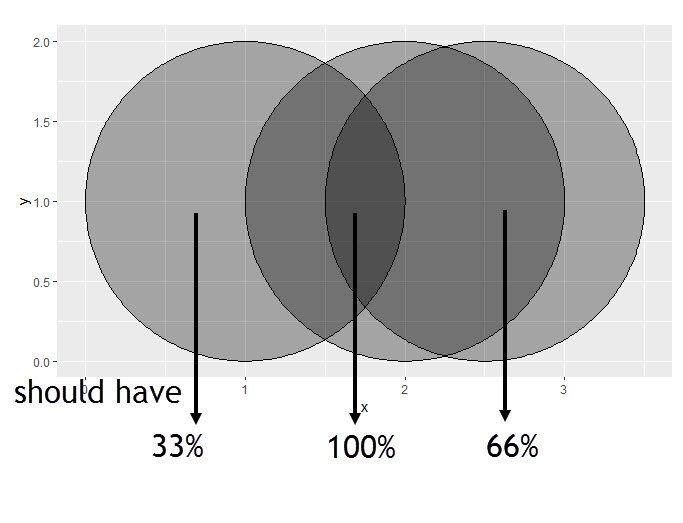
Установите непрозрачность значений серого перекрывающихся областей относительно n
Я изо всех сил пытаюсь понять (и контролировать) смешивание альф - к сожалению, альфа-значения не просто "складываются" (0,5 + 0,5 - это не 1). Но как мне этого достичь?
Цель состоит в том, чтобы определить (абсолютное) значение серого в перекрывающихся областях относительно общего количества наблюдений. Смотрите пример ниже.
Я пытался установить scale_alpha(range = c(0,1)) безрезультатно, может я не правильно его использовал.
library(ggplot2)
library(ggforce)
grid_df = data.frame(x = c(1:2, 2.5), y = rep(1,3), r = 1)
ggplot()+
geom_circle(data = grid_df, mapping = aes(x0 = x, y0 = y, r = r), alpha = 0.33, fill = 'black') +
coord_fixed()
3 ответа
Добавляя к ответу @MKBakker, можно использовать функцию для прогнозирования итоговой альфы из любого числа слоев и значений альфа:
alpha_out <- function(alpha, num = 1) {
result = alpha
if(num == 1) return(result)
for(i in 2:num) { result = result + alpha * (1-result) }
return (result)
}
alpha_out(0.33, 1)
#[1] 0.33
alpha_out(0.33, 2)
#[1] 0.5511
alpha_out(0.33, 3)
#[1] 0.699237
Это позволяет увидеть, что альфа асимптотически приближается к 1 с большим количеством слоев.
alpha_out(0.33, 40)
#[1] 0.9999999
Если предположить, что 0,99 "достаточно близко", вам нужно использовать 0,8, чтобы получить три слоя
alpha_out(0.8, 3)
#[1] 0.992
РЕДАКТИРОВАТЬ: добавлен график результатов
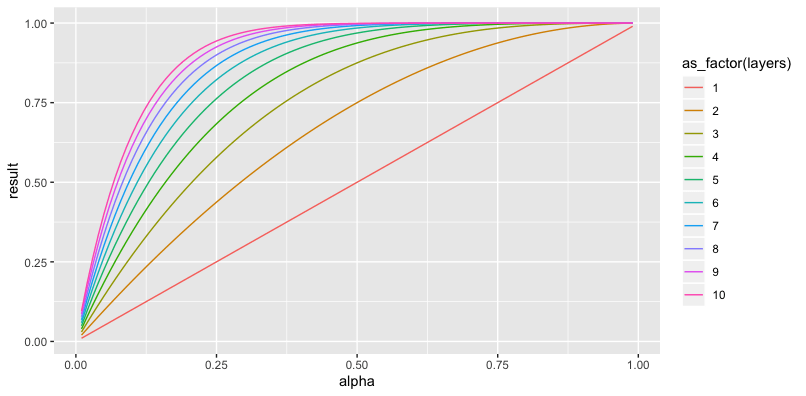
Мы можем видеть, какие результаты мы получили бы от ряда альфа-слоев и слоев:
library(tidyverse)
alpha_table <-
tibble(
alpha = rep(0.01*1:99, 10),
layers = rep(1:10, each = 99)
)
alpha_table <- alpha_table %>%
rowwise() %>%
mutate(result = alpha_out(alpha, layers))
ggplot(alpha_table, aes(alpha, result, color = as_factor(layers),
group = layers)) +
geom_line()
И мы также можем увидеть, сколько альфа нам нужно, чтобы пройти порог комбинированной непрозрачности, учитывая каждое количество слоев. Например, вот сколько альфы вам нужно, чтобы достичь общей непрозрачности 0,99 для данного количества слоев. Для 5 слоев вам нужно alpha = 0.61, например.
alpha_table %>%
group_by(layers) %>%
filter(result >= 0.99) %>%
slice(1)
## A tibble: 10 x 3
## Groups: layers [10]
# alpha layers result
# <dbl> <int> <dbl>
# 1 0.99 1 0.99
# 2 0.9 2 0.99
# 3 0.79 3 0.991
# 4 0.69 4 0.991
# 5 0.61 5 0.991
# 6 0.54 6 0.991
# 7 0.49 7 0.991
# 8 0.44 8 0.990
# 9 0.41 9 0.991
#10 0.37 10 0.990
Все это говорит о том, что я не думаю, что есть простая реализация, чтобы получить то, что вы ищете. Если вы хотите 100% темного в перекрывающейся области, вы можете попробовать эти подходы:
манипулирование изображением после факта (возможно, выполнимо с помощью
imagemagick) применить кривую яркости, чтобы сделать темные области на 100% черными, а остальные масштабировать до ожидаемых уровней темноты.преобразовать график в
sfвозьмите объект и проанализируйте фигуры, чтобы посчитать, сколько фигур перекрывается в любой заданной точке. Затем вы можете вручную сопоставить их с уровнями темноты, которые вы хотите.
Во-первых, +1 к @JonSpring - это всего лишь расширение идеи в конце их ответа. Если вы делаете sf объект, вы можете легко получить пересечения полигонов. В результате вы получаете не сами круги, а многоугольники, возникающие в результате разделения пересекающихся частей.
Начиная с вашей сетки, сделайте точку для каждой строки, преобразуйте это в sf фрейм данных, затем возьмите буфер точек с радиусом, указанным в столбце r, Это превращает каждую точку в окружность с центром в координатах точки и является гибкой для разных радиусов. Между 3 кружками находятся 6 пересекающихся многоугольников, как показано в результате.
library(dplyr)
library(sf)
library(ggplot2)
library(ggforce)
grid_df <- data.frame(x = c(1:2, 2.5), y = rep(1,3), r = 1)
grid_sf <- grid_df %>%
mutate(geometry = purrr::map2(x, y, ~st_point(c(.x, .y)))) %>%
st_as_sf() %>%
st_buffer(dist = .$r, nQuadSegs = 60) %>%
st_intersection()
grid_sf
#> Simple feature collection with 6 features and 5 fields
#> geometry type: GEOMETRY
#> dimension: XY
#> bbox: xmin: 0 ymin: 0 xmax: 3.5 ymax: 2
#> epsg (SRID): NA
#> proj4string: NA
#> x y r n.overlaps origins geometry
#> 1 1.0 1 1 1 1 POLYGON ((1.5 0.1339746, 1....
#> 1.1 1.0 1 1 2 1, 2 POLYGON ((1.75 0.3386862, 1...
#> 2 2.0 1 1 1 2 MULTIPOLYGON (((2.258819 0....
#> 1.2 1.0 1 1 3 1, 2, 3 POLYGON ((2 1, 1.999657 0.9...
#> 2.1 2.0 1 1 2 2, 3 POLYGON ((3 1, 2.999657 0.9...
#> 3 2.5 1 1 1 3 MULTIPOLYGON (((3.5 1, 3.49...
Используйте это n.overlaps столбец, который исходит от st_intersection назначить альфа. По умолчанию альфа будет масштабироваться от 0 до 1, но я полагаю, что вы на самом деле не хотите 0 альфа для внешних неперекрывающихся частей окружностей, поэтому я масштабирую его, чтобы получить минимальную альфа.
alpha_range <- range(grid_sf$n.overlaps) / max(grid_sf$n.overlaps)
grid_sf %>%
ggplot() +
geom_sf(aes(alpha = n.overlaps), fill = "black") +
scale_alpha(range = alpha_range)

Просто чтобы немного расширить и сделать различные многоугольники более четкими, взгляните с дискретной шкалой заливки вместо альфа:
grid_sf %>%
ggplot() +
geom_sf(aes(fill = as.factor(n.overlaps))) +
scale_fill_brewer(palette = "YlGnBu")

Альфа может быть добавлена с использованием следующего подхода ( https://en.wikipedia.org/wiki/Alpha_compositing)
Альфа двух слитых фигур рассчитывается следующим образом:
A (out) = A (src) + A (dst) * 1-A (src)
Следовательно, для A(src) = A(dst) = 0,33 получаем:
x = 0.33
y = x + x*(1-x)
y
[1] 0,5511
И если у нас есть три формы, с A = 0,33, мы индуцируем:
y = x + x*(1-x) + x*(1-(x + x*(1-x)))
y
[1] 0.699237
Я мог бы продолжить о том, какие значения приведут к 1 при добавлении 2 или 3 фигур вместе, но самый полезный комментарий - то, что альфы не объединяются аддитивным способом.