Почему вершина раскрашивает NP-сложно?
Я читаю алгоритм раскраски вершин. Я вижу документы, объясняющие, как решить проблему, используя BFS (подразумевая, что проблема может быть решена в O(|V|+|E|)). Но я также вижу, что упоминается, что это NP-трудная проблема.
Как эти два подходят друг другу? Не могли бы вы пролить немного света?
Вот алгоритм, с которым я столкнулся, который выглядел для меня как полиномиальное решение общего случая:
Имейте каждый цвет, идентифицированный числом. Начните с узла и назначьте ему цвет с наименьшим номером. Посетите каждого из его соседей, используя BFS. При посещении узла проверьте цвет каждого из его соседей и назначьте цвет с наименьшим номером, который не назначен ни одному из его соседей.
Сказано, что подход BFS работает только для 2 цветов. Я не могу понять, почему вышеупомянутая техника не будет работать для более чем 2 цветов
3 ответа
Обычно, когда я думаю о поиске с использованием хлеба (BFS), я думаю, что он применяется к деревьям, но раскраска вершин - это проблема графа, а не дерева. Я полагаю, что вы можете применить BFS к графу, приняв правило, что все узлы, смежные с текущим, помечаются перед переходом на другой узел.
Сначала рассмотрим простой пример того, как не работает простая маркировка с использованием упорядочения по наименьшему числу (так называемое последовательное упорядочение):
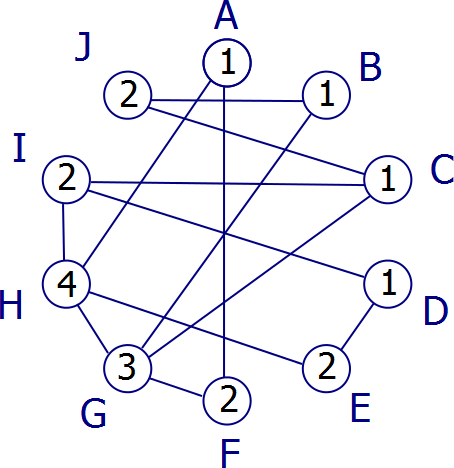
Если мы помечаем узлы в порядке по часовой стрелке (от A до J), мы получаем 4-раскраску, тогда как на самом деле этот граф имеет 2-раскраску. Теперь ваше правило приоритизации надписей на соседних узлах будет работать, потому что это двухцветная. Но есть 3 раскраски, для которых ваше правило не будет работать, например:
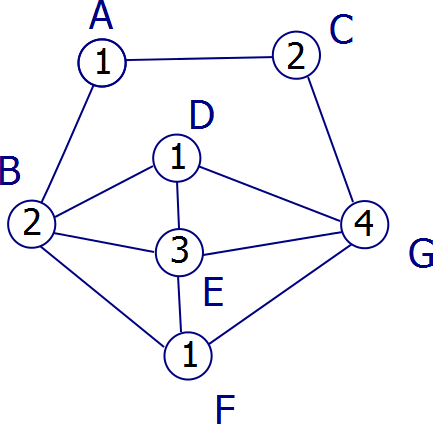
В этом примере мы выбираем A в качестве корня "дерева" и сначала делаем его дочерние элементы, B и C. Затем мы выбираем дочерний элемент B, поскольку он имеет более низкий алфавитный порядок, чем C, и делаем все дочерние элементы B. В итоге получается 4-цветная раскраска, когда на самом деле график может быть 3-цветным.
Особый случай раскраски вершин или аппроксимация может быть достигнута с использованием BFS. Общая проблема - NP-Complete, и BFS не может решить каждый ее случай. Я бы хотел привести контрпример, но в вашем описании алгоритма отсутствует - стратегия раскраски не ясна.
Например, простая раскраска, достижимая с помощью BFS: c(v) = d(source,v) (здесь c(v) это цвет, d(source,v) это расстояние от источника до вершины, полученное с помощью BFS)).
Легко видеть, что это не оптимально для A--B--C--D, где вы можете покрасить его в 2 цвета, но это решение использует 4 цвета.
Алгоритм, использующий BFS, решает ослабленный случай проблемы раскраски вершин, когда число цветов не фиксировано, и иногда он может работать как приближенное решение из общей полной задачи NP, состоящей в том, чтобы раскрасить график с использованием k цветов или найти минимальный набор цветов, который можно использовать для раскраски графика