Постепенно сохраняйте путь от корневого узла к узлу многолучевого дерева во время вставки, чтобы операция хранения не имела сложности O(n)
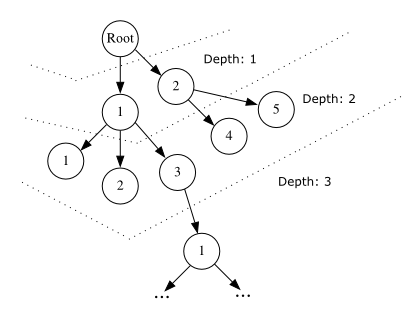
Я хотел бы спросить, знает ли кто-нибудь эффективный способ сохранить путь от корневого узла к новому узлу многострочного дерева во время вставки нового узла. Например, если у меня есть следующее дерево:
Для каждого узла в настоящее время я сохраняю массив пути к узлу от корневого узла во время вставки следующим образом, назначая уникальный int Удостоверение личности каждого ребенка на одной глубине:
Root node -> [1]
Depth 1, child 1 of root -> [1, 1]
Depth 1, child 2 of root -> [1, 2]
Depth 2, child 1 of parent 1 -> [1, 1, 1]
Depth 2, child 2 of parent 1 -> [1, 1, 2]
Depth 2, child 3 of parent 1 -> [1, 1, 3]
Depth 2, child 1 of parent 2 -> [1, 2, 4]
Depth 2, child 2 of parent 2 -> [1, 2, 5]
Depth 3, child 1 of parent 3 -> [1, 1, 3, 1]
...
Если я сейчас вставлю новый узел из конечного узла 1 на глубине 3, я должен был бы создать новый массив пути для него, хранящий все узлы родителя 1 (т.е. [1, 1, 3, 1]) плюс новый идентификатор ребенка, который 1 для первого ребенка:
Depth 4, child 1 of parent 1 -> [1, 1, 3, 1, 1]
Поскольку мое дерево сильно растет в росте (число дочерних элементов на глубину относительно мало, но глубина может быть высокой), медленной частью этого алгоритма будет процесс восстановления массива. Просто представьте дерево глубины 1.000.000, если я вставлю новый узел из узла глубины 1.000.000 Я должен был бы создать новый массив для этого нового узла, хранящего все 1.000.001 Идентификаторы родителя плюс добавление идентификатора нового узла:
Depth 1.000.001, child 1 of parent x -> [...1 million and one IDs... , 1]
Есть ли более эффективный способ сохранить путь на каждом узле во время вставки узла?
Мне в основном нужно это, чтобы определить, является ли какой-либо данный узел дочерним по отношению к возможному родительскому узлу в дереве, и, поскольку у меня есть путь, сохраненный в каждом узле, я легко могу это сделать, проверив массив путей дочернего элемента, например:
// Ex. 1
Is node 4 of depth 2 the parent/ancestor of node 1 of depth 3?
node 1 of depth 3 has the following path array: pathArray = [1, 1, 3, 1]
Its ancestor ID on depth 2 is: pathArray[2] -> 3
3 != 4 and therefore I know that node 4 of depth 2
is not a parent of node 1 of depth 3.
// Ex. 2
Is node 1 of depth 1 the parent/ancestor of node 1 of depth 3?
node 1 of depth 3 has the following path array: pathArray = [1, 1, 3, 1]
Its ancestor ID on depth 1 is: pathArray[1] -> 1
1 == 1 and therefore I know that node 1 of depth 1
is a parent of node 1 of depth 3.
Эта операция поиска будет быстрой, проблема заключается в создании массива пути по мере того, как дерево углубляется.
Мы ценим любые предложения.
Спасибо за внимание.
3 ответа
Прямо сейчас ваше решение имеет O(1) время поиска, O(h) введите время и O(n^2) космическая выпуклость, где n это количество узлов и h это высота, которая не более n,
Вы можете достичь компромисса с O(log n) уважать, O((log n)^2) вставить и O(n log n) пространство следующим образом:
Пусть каждый узел хранит один указатель перехода на каждого из своих предков с расстояния 1 (его родитель), 2 (дедушка), 4 (дедушка и дедушка), 8, 16 и т. Д., Пока корень не будет достигнут или пройден. Максимальное расстояние от любого узла до корня nтак что для каждого узла вы храните O(log n) прыгать-указатели. Поскольку вы делаете это для каждого узла, общая сложность пространства O(n log n),
Отвечая на вопрос о том, y является предком x тривиально, если y не имеет более низкой глубины, чем x, Назовите глубину узлов dy а также dx, Вы знаете, что если y является предком xтогда это dx-dyпредок x, То есть если dy = 5 а также dx = 17Знаете, если y является xпредок, то это 17 - 5 уровни выше x,
Следовательно, вы можете выполнять поиск, рекурсивно прыгая на максимально возможное расстояние вверх по дереву из x не выходя за пределы целевого предка. Например, если вы начинаете с глубины 16 и хотите найти предка на глубине 6, вам интересны предки на 10 уровней выше. Вы не можете прыгнуть на 16 уровней выше, так как это приведет к превышению заданного предка, поэтому вместо этого вы прыгаете на 8. Теперь вы находитесь на глубине 16-8=8, а оставшееся расстояние до целевого предка, которое равно 6, равно 2. Так как есть указатель, который поднимается ровно на два шага вверх, вы следуете этому и достигли целевой предок.
Каждый раз, когда вы следите за указателем вверх по дереву, вы получаете по крайней мере половину пути к своей цели, поэтому максимальное количество указателей, за которыми вы можете следовать, O(log n),
При вставке узла e как ребенок другого узла x вы можете построить eпрыжковые указатели, находя xпредки с расстояния 1, 3, 7, 15 и т. д. (с e на один уровень дальше от всех этих, чем x является). Есть O(log n)такие поиски. Как мы уже говорили выше, каждый из поисков занимает O(log n) время. Таким образом, общая сумма O((log n)^2),
Эту операцию можно было бы сделать еще быстрее, сохранив некоторую дополнительную информацию, но я не могу понять, как именно сейчас.
ПРИМЕЧАНИЕ. Эта идея на самом деле является частью классического решения проблемы предка уровня. Классическое решение позволяет искать, как вы описали их в O(1) время, сохраняя при этом пространство всей структуры данных O(n), Однако структура данных является статической, поэтому в решении не указано, как выполнять вставки. Возможно, есть способ адаптировать предка уровня к динамическому сценарию и получить лучшее время выполнения, чем я описал здесь, но я не уверен, как это сделать.
Сопоставьте свои узлы в HashMap<node-id, node> ,
Теперь, когда вам нужно
определить, является ли какой-либо данный узел дочерним по отношению к возможному родительскому узлу,
Вы можете найти точное местоположение этого узла в дереве из HashMap, а затем переместиться обратно вверх по дереву, используя родительские указатели, чтобы увидеть, лежит ли возможный родительский путь на пути к корню.
В достаточно сбалансированном дереве это будет O(Log n) времени выполнения (для обхода дерева) и O (n) пространства (из HashMap).
Если вы идете с вашим текущим планом хранения пути от каждого узла к корню, то у вас будет O(Log n) времени выполнения (при условии сбалансированного дерева) и O(n * Log n) пространства для хранения длины Log n путь для каждого из n узлов.
Массивы хранят все свои значения в памяти. Если вы хотите сохранить эту собственность, вы должны их использовать. Или, если у вас все в порядке с переходом по нескольким ячейкам памяти, вы можете хранить в каждом узле только его непосредственного родителя и отслеживать до необходимого уровня для выполнения требуемой проверки.