Python - расчет трендовых линий с ошибками

Question

Таким образом, у меня есть некоторые данные, хранящиеся в виде двух списков, и нанесли их на график, используя

plot(datasetx, datasety)

Тогда я установил линию тренда

trend = polyfit(datasetx, datasety)
trendx = []
trendy = []

for a in range(datasetx[0], (datasetx[-1]+1)):
    trendx.append(a)
    trendy.append(trend[0]*a**2 + trend[1]*a + trend[2])

plot(trendx, trendy)

Но у меня есть третий список данных, который является ошибкой в ​​исходном наборе данных. Я в порядке с построением графиков ошибок, но я не знаю, как использовать это, как найти ошибку в коэффициентах полиномиальной линии тренда.

Итак, скажем, моя линия тренда оказалась 5x^2 + 3x + 4 = y, должна быть какая-то ошибка в значениях 5, 3 и 4.

Есть ли инструмент, использующий NumPy, который рассчитает это для меня?

Answer 1

Я думаю, что вы можете использовать функцию curve_fit из scipy.optimize ( документация). Базовый пример использования:

import numpy as np
from scipy.optimize import curve_fit

def func(x, a, b, c):
    return a*x**2 + b*x + c

x = np.linspace(0,4,50)
y = func(x, 5, 3, 4)
yn = y + 0.2*np.random.normal(size=len(x))

popt, pcov = curve_fit(func, x, yn)

Следуя документации, pcov дает:

Расчетная ковариация поп. Диагонали обеспечивают дисперсию оценки параметра.

Таким образом, вы можете рассчитать оценку погрешности по коэффициентам. Чтобы получить стандартное отклонение, вы можете взять квадратный корень из дисперсии.

Теперь у вас есть ошибка в коэффициентах, но она основана только на отклонении между данными и подгонкой. Если вы также хотите учесть ошибку в самих данных, curve_fit Функция обеспечивает sigma аргумент:

сигма: нет или N-длина последовательности

Если не None, оно представляет стандартное отклонение ydata. Этот вектор, если он задан, будет использоваться в качестве весов в задаче наименьших квадратов.

Полный пример:

import numpy as np
from scipy.optimize import curve_fit

def func(x, a, b, c):
    return a*x**2 + b*x + c

x = np.linspace(0,4,20)
y = func(x, 5, 3, 4)
# generate noisy ydata
yn = y + 0.2 * y * np.random.normal(size=len(x))
# generate error on ydata
y_sigma = 0.2 * y * np.random.normal(size=len(x))

popt, pcov = curve_fit(func, x, yn, sigma = y_sigma)

# plot
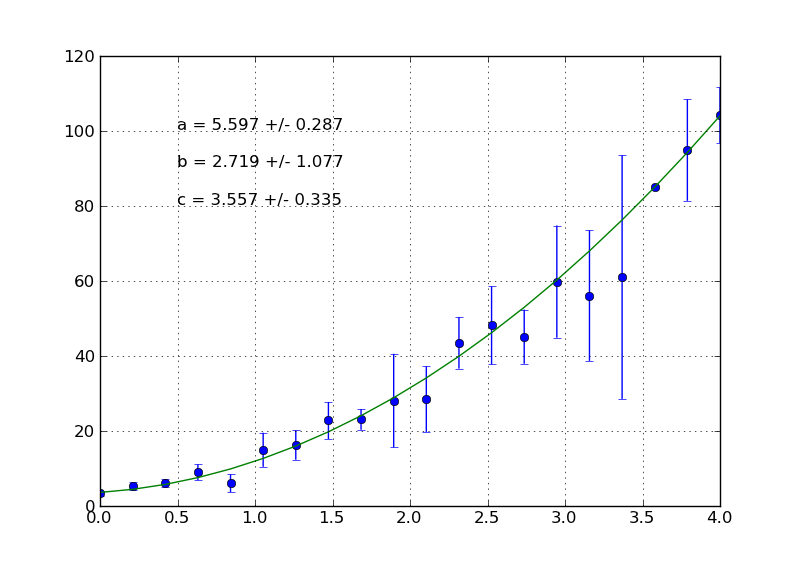
import matplotlib.pyplot as plt

fig = plt.figure()
ax = fig.add_subplot(111)
ax.errorbar(x, yn, yerr = y_sigma, fmt = 'o')
ax.plot(x, np.polyval(popt, x), '-')
ax.text(0.5, 100, r"a = {0:.3f} +/- {1:.3f}".format(popt[0], pcov[0,0]**0.5))
ax.text(0.5, 90, r"b = {0:.3f} +/- {1:.3f}".format(popt[1], pcov[1,1]**0.5))
ax.text(0.5, 80, r"c = {0:.3f} +/- {1:.3f}".format(popt[2], pcov[2,2]**0.5))
ax.grid()
plt.show()

---

Затем еще кое-что об использовании массивов numpy. Одним из основных преимуществ использования numpy является то, что вы можете избежать циклов for, поскольку операции над массивами применяются поэлементно. Таким образом, цикл for в вашем примере также может быть выполнен следующим образом:

trendx = arange(datasetx[0], (datasetx[-1]+1))
trendy = trend[0]*trendx**2 + trend[1]*trendx + trend[2]

Где я использую arange вместо диапазона, так как он возвращает пустой массив вместо списка. В этом случае вы также можете использовать функцию NumPy polyval:

trendy = polyval(trend, trendx)

Answer 2

Я не смог найти какой-либо способ получить ошибки в коэффициентах, которые встроены в NumPy или Python. У меня есть простой инструмент, который я написал на основе Разделов 8.5 и 8.6 из " Введение в анализ ошибок" Джона Тейлора. Возможно, этого будет достаточно для вашей задачи (обратите внимание, что по умолчанию возвращается дисперсия, а не стандартное отклонение). Вы можете получить большие ошибки (как в приведенном примере) из-за значительной ковариации.

def leastSquares(xMat, yMat):
'''
Purpose
-------
Perform least squares using the procedure outlined in 8.5 and 8.6 of Taylor, solving
matrix equation X a = Y

Examples
--------
>>> from scipy import matrix
>>> xMat = matrix([[  1,   5,  25],
                   [  1,   7,  49],
                   [  1,   9,  81],
                   [  1,  11, 121]])
>>> # matrix has rows of format [constant, x, x^2]
>>> yMat = matrix([[142],
                   [168],
                   [211],
                   [251]])
>>> a, varCoef, yRes = leastSquares(xMat, yMat)
>>> # a is a column matrix, holding the three coefficients a, b, c, corresponding to
>>> # the equation a + b*x + c*x^2

Returns
-------
a: matrix
    best fit coefficients
varCoef: matrix
    variance of derived coefficents
yRes: matrix
    y-residuals of fit 
'''
xMatSize = xMat.shape
numMeas = xMatSize[0]
numVars = xMatSize[1]

xxMat = xMat.T * xMat
xyMat = xMat.T * yMat
xxMatI = xxMat.I

aMat = xxMatI * xyMat
yAvgMat = xMat * aMat
yRes = yMat - yAvgMat

var = (yRes.T * yRes) / (numMeas - numVars)
varCoef = xxMatI.diagonal() * var[0, 0]

return aMat, varCoef, yRes