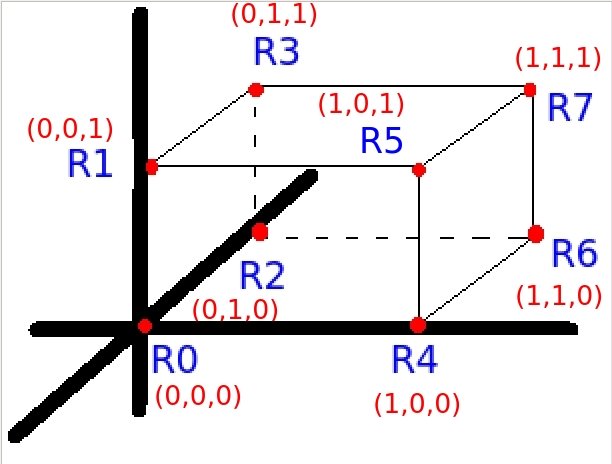
MPI_Cart_Shift.Corner Neighborhood
Мне нужно создать коммуникатор с топологией куба, а затем выбрать грань куба, используя реализованный обмен сообщениями MPI_Cart_Shift между процессами, которые находятся на грани. Например, я обрабатываю с рангом 0(R0), мои окрестности R2, R4, R6(нижняя грань куба). Я могу найти R2 и R4, но я не могу понять, как найти R6. Мой код:
#include<mpi.h>
#include<stdio.h>
int main(int argc, char *argv[])
{
int rank, k;
int size;
int ndims = 3;
int source, dest;
int up,down,right,left,up3, down3;
int edges[6][4] = {{0,1,5,4},
{4,5,7,6},
{2,3,1,0},
{6,7,3,2},
{1,3,7,5},
{0,2,6,7}};
int t, incep=0;
char processor_name[MPI_MAX_PROCESSOR_NAME];
MPI_Comm comm, comm3d;
int dims[3]={0,0,0}, coords[3]={0,0,0},
periods[3]={1,1,1}, reorder = 0;
MPI_Status status;
int user_edge;
MPI_Init(&argc, &argv);
MPI_Comm_size(MPI_COMM_WORLD, &size);
MPI_Comm_rank(MPI_COMM_WORLD, &rank);
MPI_Dims_create(size, ndims, dims);
MPI_Cart_create(MPI_COMM_WORLD, ndims, dims, periods, reorder, &comm);
MPI_Cart_coords(comm, rank, 3, coords);
fflush(stdout);
printf("Rank %d coordinates are %d %d %d\n", rank, coords[0], coords[1], coords[2]);
MPI_Barrier(comm);
int leftrank, rightrank;
int downrank, uprank;
MPI_Comm_rank(comm, &rank);
MPI_Cart_coords(comm, rank, 2, coords);
MPI_Cart_shift(comm, 0, -1, &downrank, &uprank);
MPI_Sendrecv(buffer, 10, MPI_INT, downrank, 123, buffer2, 10, MPI_INT, uprank, 123, comm, &status);
MPI_Cart_shift(comm, 1, -1, &rightrank, &leftrank);
MPI_Sendrecv(buffer, 10, MPI_INT, leftrank, 123, buffer2, 10, MPI_INT, rightrank, 123, comm, &status);
printf("P:%d My neighbors are rightRank: %d downRank:%d leftRank:%d upRank:%d diagonal:%d diagonalX:%d\n", rank,rightrank,downrank,leftrank,uprank,diagonal,diagonalX);
MPI_Finalize();
return 0;
}
Я постараюсь добавить что-то вроде этого MPI_Cart_shift(comm, 2, 1, &diagonal, &diagonalX); Но для R0 это показывает мне R1, и это я понимаю.... Как я могу получить угловые окрестности?
3 ответа
Вы можете использовать MPI_Cart_rank, чтобы найти необходимую информацию.
int MPI_Cart_rank(MPI_Comm comm, const int coords[], int *rank)
Здесь comm - коммуникатор с декартовой топологией. Координаты - это целочисленный массив (размер этого массива равен числу измерений декартовой топологии), содержащий координаты процесса (в вашем случае 1,1,0 для R6). Тогда выходной ранг вернет глобальный ранг того процесса, который вы можете использовать в последующем общении.
Кстати, MPI_Cart_coords выполняет противоположное направление, то есть от ранга до координаты.
MPI_Cart_shift Вы можете найти соседей только в любом из основных направлений, но не по диагонали - вы должны реализовать это самостоятельно, что не так сложно сделать. Само декартово смещение - не более чем удобная функция, которая оборачивает вызовы MPI_Cart_coords а также MPI_Cart_rank:
//
// The following is equivalent to
// MPI_Cart_shift(cart_comm, i, disp, &rank_source, &rank_dest);
//
// Obtain the rank of the calling process and translate it into coordinates
int rank, coords[ndims];
MPI_Comm_rank(cart_comm, &rank);
MPI_Cart_coords(cart_comm, rank, ndims, coords);
int mycoord_i = coords[i];
// Compute the coordinates of the destination in direction i and convert them into rank
coords[i] = mycoord_i + disp;
// Take care of non-periodic dimensions
if (!periods[i] && (coords[i] >= dims[i] || coords[i] < 0))
rank_dest = MPI_PROC_NULL;
else
MPI_Cart_rank(cart_comm, coords, &rank_dest);
// Compute the coordinates of the source in direction i and convert them into rank
coords[i] = mycoord_i - disp;
// Take care of non-periodic dimensions
if (!periods[i] && (coords[i] >= dims[i] || coords[i] < 0))
rank_source = MPI_PROC_NULL;
else
MPI_Cart_rank(cart_comm, coords, &rank_source);
Обратите внимание на то, как выход из-за границы должен быть явно обработан для непериодических измерений. Для периодических MPI_Cart_rank Сам делает складывание координат. Ваша декартова топология является периодической, поэтому проверки могут быть пропущены (не рекомендуется).
Вы можете легко адаптировать приведенный выше код для создания сдвига в двух или более измерениях, а затем использовать его для перечисления всех возможных комбинаций смещений и направлений, чтобы найти ранги, лежащие на заданной грани. Например:
int rank, coords[ndims];
MPI_Comm_rank(cart_comm, &rank);
MPI_Cart_coords(cart_comm, rank, ndims, coords);
int my_coord1 = coords[1];
int my_coord2 = coords[2];
coords[1] = my_coord1 + 1;
coords[2] = my_coord2 + 1;
MPI_Cart_rank(cart_comm, coords, &rank_dest);
coords[1] = my_coord1 - 1;
coords[2] = my_coord2 - 1;
MPI_Cart_rank(cart_comm, coords, &rank_source);
даст вам звание R6 в rank_dest когда выполняется R0. Если вы извлекаете код в отдельной подпрограмме и вызываете его MyMPI_Cart_shift2:
MyMPI_Cart_shift2(cart_comm, 1, 1, 2, 1, &rank_source, &rank_dest);
Другой вариант будет использовать MPI_Cart_sub разделить декартову топологию на плиты, параллельные лицу. Затем вы можете напрямую осуществлять связь, включающую только звания в любой данной плите.
Вы забыли обозначить R5. Существует не прямой подход, который я могу придумать. Но вот косвенный путь:
(1) Для любого ранга, координаты которого (A,y,z) рассмотреть координаты: (A,y+1,z+1), (A,y-1,z-1), (A,y+1,z-1) а также (A,y-1,z+1) - это могут быть 4 диагональных соседа. Понятно, что при рассмотрении минуса, например, z-1, ясно, что z-1 >= 0 и при рассмотрении плюс, например, y+1 <= (dimension_in_y - 1), Например, рассмотрим R5 (который вы забыли обозначить). R5 в соответствии с MPI имеет координаты R5(0,1,0), Может иметь 4 соседей по диагонали: (0,1+1,0+1), (0,1-1,0-1),(0,1+1,0-1),(0,1-1,0+1) - из которых существует только четвертый (ясно, что ни у какого соседа не может быть отрицательных координат, и каждая координата должна быть на 1 меньше, чем размерность в этом направлении). Далее просто запрос MPI_coordinate_to_rank(),
(2) Другой метод заключается в запросе right а также left соседи о своих front а также back соседи (это будет плохо с точки зрения производительности).
(3) Чтобы обобщить его на 8 соседей - вам нужно будет также изменить координату X - но ваш вопрос ограничен гранью куба.