Mathematica "связанные списки" и производительность

Question

В Mathematica я создаю односвязные списки примерно так:

toLinkedList[x_List] := Fold[pair[#2, #1] &, pair[], Reverse[x]];

fromLinkedList[ll_pair] := List @@ Flatten[ll];

emptyQ[pair[]] := True;
emptyQ[_pair] := False;    

Используя символ pair для минусов клетки имеет преимущество Flatten работать безопасно, даже если списки содержат стиль Mathematica List s, и позволяет вам определять пользовательские обозначения, используя MakeExpression / MakeBoxes, что делает все намного приятнее. Во избежание необходимости возиться с $IterationLimit Я написал функции для работы с этими списками, используя либо While петли или NestWhile вместо использования рекурсии. Естественно, я хотел посмотреть, какой подход будет быстрее, поэтому я написал два кандидата, чтобы я мог посмотреть их бой:

nestLength[ll_pair] := 
 With[{step = {#[[1, -1]], #[[-1]] + 1} &},
  Last@NestWhile[step, {ll, 0}, ! emptyQ@First@# &]];

whileLength[ll_pair] := 
 Module[{result = 0, current = ll},
  While[! emptyQ@current,
   current = current[[2]];
   ++result];
  result];

Результаты были очень странными. Я проверил функции в связанных списках длиной 10000, и whileLength обычно был примерно на 50% быстрее, примерно за 0,035 секунды до nestLength 0,055 секунды. Однако иногда whileLength займет около ~4 секунд. Я подумал, что может быть какое-то поведение при кэшировании, поэтому я начал генерировать новые случайные списки для проверки и whileLength не обязательно будет медленным при первом запуске с новым списком; это может занять десятки раз, чтобы увидеть замедление, но тогда оно не повторится (по крайней мере, не для 200 прогонов, которые я пробовал с каждым списком).

Что может происходить?

Для справки, функция, которую я использовал для тестирования:

getTimes[f_, n_] :=
 With[{ll = toLinkedList@RandomInteger[100, 10000]},
  Table[Timing[f@ll], {n}][[All, 1]]]

РЕДАКТИРОВАТЬ: я забыл упомянуть версию ранее; Я получил эти результаты с Mathematica 8.

РЕДАКТИРОВАТЬ второе: когда я прочитал ответ Даниэля Лихтблау, я понял, что в моих временах для "типичных" забегов опережал 0. Это было исправлено.

РЕДАКТИРОВАТЬ третий: я думаю, что Леонид Шифрин правильно связать проблему с Module; Я могу получить такое же поведение от NestWhile версия, заменив With с Module:

nestModuleLength[ll_pair] := 
  Module[{step = {#[[1, -1]], #[[-1]] + 1} &}, 
   Last@NestWhile[step, {ll, 0}, ! emptyQ@First@# &]];

In[15]:= Select[getTimes[nestModuleLength, 100], # > 3 &]
Out[15]= {3.797}

Answer 1

Приведенные ниже примеры дают типичные результаты.

Один медленный пример в 20 пробежек.

In[18]:= getTimes[whileLength, 20]

Out[18]= {0.031, 0.032, 0.031, 0.031, 0.031, 0.032, 0.031, 0.031, \
0.031, 0.047, 0.032, 0.031, 0.031, 3.547, 0.047, 0.031, 0.031, 0.032, \
0.031, 0.031}

Попутно отмечу, что время примерно в 10 раз выше, чем в оригинальном сообщении, за исключением медленных случаев, которые сравнимы. Не уверен, что объясняет эту разницу в соотношениях.

Нет медленных примеров.

In[17]:= getTimes[nestLength, 20]

Out[17]= {0.047, 0.047, 0.062, 0.047, 0.047, 0.062, 0.047, 0.047, \
0.047, 0.063, 0.046, 0.047, 0.047, 0.063, 0.047, 0.046, 0.047, 0.063, \
0.047, 0.047}

Один медленный пример на 100 пробежек.

In[19]:= getTimes[whileLength, 100]

Out[19]= {0.031, 0.031, 0.031, 0.032, 0.031, 3.594, 0.047, 0.031, \
0.031, 0.031, 0.032, 0.031, 0.031, 0.031, 0.032, 0.031, 0.047, 0.031, \
0.031, 0.031, 0.032, 0.031, 0.031, 0.031, 0.032, 0.047, 0.031, 0.031, \
0.031, 0.032, 0.031, 0.031, 0.031, 0.032, 0.031, 0.031, 0.047, 0.031, \
0.031, 0.032, 0.031, 0.031, 0.031, 0.032, 0.031, 0.031, 0.047, 0.031, \
0.032, 0.031, 0.031, 0.031, 0.032, 0.031, 0.031, 0.047, 0.031, 0.031, \
0.032, 0.031, 0.031, 0.031, 0.032, 0.031, 0.047, 0.031, 0.031, 0.032, \
0.031, 0.031, 0.031, 0.032, 0.031, 0.031, 0.031, 0.032, 0.046, 0.032, \
0.031, 0.031, 0.031, 0.032, 0.031, 0.031, 0.047, 0.031, 0.032, 0.031, \
0.031, 0.031, 0.032, 0.031, 0.047, 0.031, 0.031, 0.031, 0.032, 0.031, \
0.031, 0.031}

Mathematica несовершенно реализует то, что называется "бесконечной оценкой". То есть выражение переоценивается до тех пор, пока оно не перестанет изменяться. Чтобы сделать это достаточно быстро, существуют различные оптимизации, которые пытаются замкнуть процесс, когда это возможно.

В некоторых случаях это может быть сложно различить (из-за эффекта, похожего на хеш-коллизии), и выражения могут быть излишне переоценены. Глубоко вложенные выражения имеют тенденцию быть худшим случаем для этого. У нас есть дополнительный код, который часто решает эти проблемы даже в случае коллизий.

В этом случае виновником является именно этот код, который пытается быстро определить, требует ли выражение переоценки. Это странно, но, возможно, подсказка (кому-то), что это происходит не чаще одного раза в цикле "В то время как". Так что в плохих случаях что-то происходит, что предотвращает повторение, пока внутри того же Пока.

Одно время я был знаком с кодом обнаружения переоценки, написав его фрагмент. Но он был переписан для версии 8. Так что даже после того, как я увидел это неоптимальное поведение в отладчике, для меня это загадка. Все, что я могу сейчас сказать, это то, что я подал отчет об ошибке.

Как заметил Леонид Шифрин, символы с атрибутом HoldAllComplete неуязвимы для этой проблемы. Поэтому использование этого атрибута может быть полезным для этого типа кода.

Даниэль Лихтблау Вольфрам Исследования

Answer 2

Отказ от ответственности: следующее является спекуляцией. Похоже, это связано с поиском UpValues, Похоже, что это было оптимизировано для глобальных переменных (так что система пропускает этот шаг, когда она может определить, что она может это сделать), но не для Module сгенерированные локальные переменные. Чтобы проверить это, назначьте HoldAllComplete приписывать pairи эффект исчезает (с тех пор UpValues не проверяются на current):

SetAttributes[pair, HoldAllComplete];

In[17]:= ll = toLinkedList@RandomInteger[100, 10000];
Max[Table[Timing[whileLength[ll]], {1000}][[All, 1]]]

Out[18]= 0.047

НТН

Answer 3

Кажется, это связано с управлением памятью локальных символов модуля.

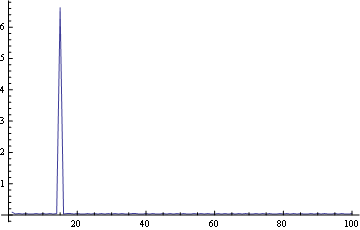
Я покажу временные ряды из некоторых прогонов. Каждый прогон, конечно, дает уникальный график, но я проверял "последовательность" между прогонами. Посмотрите:

whileLength[l2_pair] := 
  Module[{result = 0}, current = l2; 
   While[! emptyQ@current, current = current[[2]];
    ++result];
   result];  

дает следующие сроки:

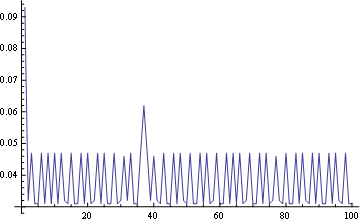
При использовании только глобальных символов:

whileLength[l2_pair] := 
  Module[{}, result = 0; current = l2; 
   While[! emptyQ@current, current = current[[2]];
    ++result];
   result];

дает: