Проверка правильности алгоритма FFT
Сегодня я написал алгоритм для вычисления быстрого преобразования Фурье из заданного массива точек, представляющих дискретную функцию. Сейчас я пытаюсь проверить, работает ли он. Я пробовал около дюжины различных наборов ввода, и они, кажется, совпадают с примерами, которые я нашел в Интернете. Тем не менее, для моего последнего теста я дал ему значение cos(i / 2) с i от 0 до 31, и я получил 3 разных результата, в зависимости от того, какой решатель я использую. Мое решение кажется наименее точным:
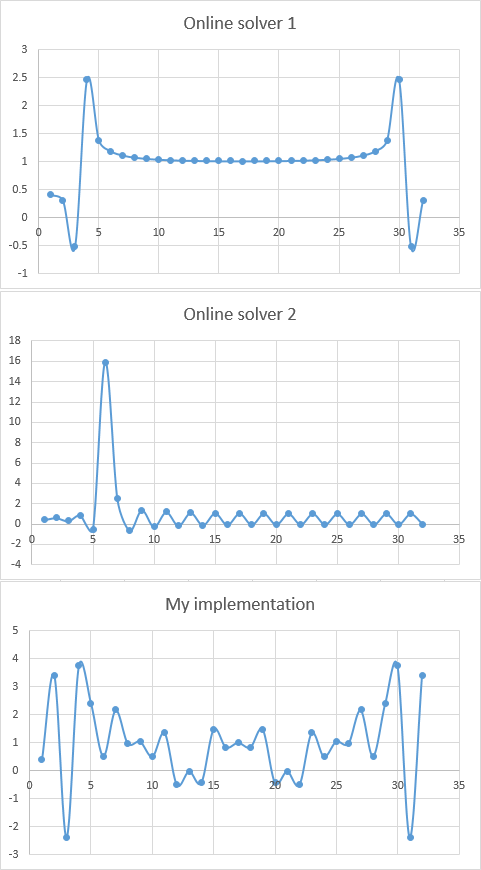
Указывает ли это на проблему с моим алгоритмом или это просто результат относительно небольшого набора данных?
Мой код ниже, на случай, если это поможет:
/**
* Slices the original array, starting with start, grabbing every stride elements.
* For example, slice(A, 3, 4, 5) would return elements 3, 8, 13, and 18 from array A.
* @param array The array to be sliced
* @param start The starting index
* @param newLength The length of the final array
* @param stride The spacing between elements to be selected
* @return A sliced copy of the input array
*/
public double[] slice(double[] array, int start, int newLength, int stride) {
double[] newArray = new double[newLength];
int count = 0;
for (int i = start; count < newLength && i < array.length; i += stride) {
newArray[count++] = array[i];
}
return newArray;
}
/**
* Calculates the fast fourier transform of the given function. The parameters are updated with the calculated values
* To ignore all imaginary output, leave imaginary null
* @param real An array representing the real part of a discrete-time function
* @param imaginary An array representing the imaginary part of a discrete-time function
* Pre: If imaginary is not null, the two arrays must be the same length, which must be a power of 2
*/
public void fft(double[] real, double[] imaginary) throws IllegalArgumentException {
if (real == null) {
throw new NullPointerException("Real array cannot be null");
}
int N = real.length;
// Make sure the length is a power of 2
if ((Math.log(N) / Math.log(2)) % 1 != 0) {
throw new IllegalArgumentException("The array length must be a power of 2");
}
if (imaginary != null && imaginary.length != N) {
throw new IllegalArgumentException("The two arrays must be the same length");
}
if (N == 1) {
return;
}
double[] even_re = slice(real, 0, N/2, 2);
double[] odd_re = slice(real, 1, N/2, 2);
double[] even_im = null;
double[] odd_im = null;
if (imaginary != null) {
even_im = slice(imaginary, 0, N/2, 2);
odd_im = slice(imaginary, 1, N/2, 2);
}
fft(even_re, even_im);
fft(odd_re, odd_im);
// F[k] = real[k] + imaginary[k]
// even odd
// F[k] = E[k] + O[k] * e^(-i*2*pi*k/N)
// F[k + N/2] = E[k] - O[k] * e^(-i*2*pi*k/N)
// Split complex arrays into component arrays:
// E[k] = er[k] + i*ei[k]
// O[k] = or[k] + i*oi[k]
// e^ix = cos(x) + i*sin(x)
// Let x = -2*pi*k/N
// F[k] = er[k] + i*ei[k] + (or[k] + i*oi[k])(cos(x) + i*sin(x))
// = er[k] + i*ei[k] + or[k]cos(x) + i*or[k]sin(x) + i*oi[k]cos(x) - oi[k]sin(x)
// = (er[k] + or[k]cos(x) - oi[k]sin(x)) + i*(ei[k] + or[k]sin(x) + oi[k]cos(x))
// { real } { imaginary }
// F[k + N/2] = (er[k] - or[k]cos(x) + oi[k]sin(x)) + i*(ei[k] - or[k]sin(x) - oi[k]cos(x))
// { real } { imaginary }
// Ignoring all imaginary parts (oi = 0):
// F[k] = er[k] + or[k]cos(x)
// F[k + N/2] = er[k] - or[k]cos(x)
for (int k = 0; k < N/2; ++k) {
double t = odd_re[k] * Math.cos(-2 * Math.PI * k/N);
real[k] = even_re[k] + t;
real[k + N/2] = even_re[k] - t;
if (imaginary != null) {
t = odd_im[k] * Math.sin(-2 * Math.PI * k/N);
real[k] -= t;
real[k + N/2] += t;
double t1 = odd_re[k] * Math.sin(-2 * Math.PI * k/N);
double t2 = odd_im[k] * Math.cos(-2 * Math.PI * k/N);
imaginary[k] = even_im[k] + t1 + t2;
imaginary[k + N/2] = even_im[k] - t1 - t2;
}
}
}
2 ответа
Проверка
посмотрите здесь: медленный DFT,iDFT в конце - моя медленная реализация DFT, и iDFT они проверены и исправлены. Я также использовал их для быстрой проверки реализаций в прошлом.
Ваш код
остановка рекурсии неверна (вы забыли установить возвращаемый элемент) моя выглядит так:
if (n<=1) { if (n==1) { dst[0]=src[0]*2.0; dst[1]=src[1]*2.0; } return; }поэтому, когда ваш
N==1установите выходной элемент вRe=2.0*real[0], Im=2.0*imaginary[0]доreturn, Также я немного заблудился в твоей сложной математике(t,t1,t2)и лень анализировать.
Просто чтобы быть уверенным, что это мое быстрое внедрение. Ему нужно слишком много вещей из иерархии классов, поэтому он не будет вам полезен, тогда как визуальное сравнение с вашим кодом.
Моя быстрая реализация (cc означает сложный вывод и ввод):
//---------------------------------------------------------------------------
void transform::DFFTcc(double *dst,double *src,int n)
{
if (n>N) init(n);
if (n<=1) { if (n==1) { dst[0]=src[0]*2.0; dst[1]=src[1]*2.0; } return; }
int i,j,n2=n>>1,q,dq=+N/n,mq=N-1;
// reorder even,odd (buterfly)
for (j=0,i=0;i<n+n;) { dst[j]=src[i]; i++; j++; dst[j]=src[i]; i+=3; j++; }
for ( i=2;i<n+n;) { dst[j]=src[i]; i++; j++; dst[j]=src[i]; i+=3; j++; }
// recursion
DFFTcc(src ,dst ,n2); // even
DFFTcc(src+n,dst+n,n2); // odd
// reorder and weight back (buterfly)
double a0,a1,b0,b1,a,b;
for (q=0,i=0,j=n;i<n;i+=2,j+=2,q=(q+dq)&mq)
{
a0=src[j ]; a1=+_cos[q];
b0=src[j+1]; b1=+_sin[q];
a=(a0*a1)-(b0*b1);
b=(a0*b1)+(a1*b0);
a0=src[i ]; a1=a;
b0=src[i+1]; b1=b;
dst[i ]=(a0+a1)*0.5;
dst[i+1]=(b0+b1)*0.5;
dst[j ]=(a0-a1)*0.5;
dst[j+1]=(b0-b1)*0.5;
}
}
//---------------------------------------------------------------------------
dst[] а также src[] не перекрываются!!! поэтому вы не можете преобразовать массив в себя._cos а также _sin предварительно вычисленные таблицы cos а также sin значения (вычисляются с помощью функции init() следующим образом:
double a,da; int i;
da=2.0*M_PI/double(N);
for (a=0.0,i=0;i<N;i++,a+=da) { _cos[i]=cos(a); _sin[i]=sin(a); }
N это сила 2 (заполненный нулями размер набора данных) (последний n от init(n) вызов)
Просто чтобы завершить здесь, мой комплексной медленной версии:
//---------------------------------------------------------------------------
void transform::DFTcc(double *dst,double *src,int n)
{
int i,j;
double a,b,a0,a1,_n,b0,b1,q,qq,dq;
dq=+2.0*M_PI/double(n); _n=2.0/double(n);
for (q=0.0,j=0;j<n;j++,q+=dq)
{
a=0.0; b=0.0;
for (qq=0.0,i=0;i<n;i++,qq+=q)
{
a0=src[i+i ]; a1=+cos(qq);
b0=src[i+i+1]; b1=+sin(qq);
a+=(a0*a1)-(b0*b1);
b+=(a0*b1)+(a1*b0);
}
dst[j+j ]=a*_n;
dst[j+j+1]=b*_n;
}
}
//---------------------------------------------------------------------------
Я бы использовал что-то авторитетное, например, Wolfram Alpha, чтобы проверить.
Если я оценю cos(i/2) за 0 <= i < 32Я получаю этот массив:
[1,0.878,0.540,0.071,-0.416,-0.801,-0.990,-0.936,-0.654,-0.211,0.284,0.709,0.960,0.977,0.754,0.347,-0.146,-0.602,-0.911,-0.997,-0.839,-0.476,0.004,0.483,0.844,0.998,0.907,0.595,0.137,-0.355,-0.760,-0.978]
Если я дам это в качестве входных данных для функции БПФ Wolfram Alpha, я получу этот результат.
Сюжет, который я получаю, выглядит симметрично, что имеет смысл. Сюжет не похож ни на один из тех, что вы предоставили.