Вычисление доверительного интервала для квантилей сначала вручную (чем в R)

Question

Было бы здорово, если бы кто-то мог проверить, правильный ли мой подход или нет. Короче вопрос будет, если ошибка расчета правильна. допустим, у меня есть следующие данные.

data = c(23.7,25.47,25.16,23.08,24.86,27.89,25.9,25.08,25.08,24.16,20.89)

Кроме того, я хочу проверить, соответствуют ли мои данные нормальному распределению.

Edit: я знаю, что есть тесты и т. Д., Но я сосредоточусь на построении qqplot с доверительными линиями. Я знаю, что в автомобильной упаковке есть метод, но я хочу понять, как строятся эти линии.

Поэтому я рассчитываю процентили для моих выборочных данных, а также для моего теоретического распределения (с оценкой mu = 24.6609а также sigma = 1.6828, Итак, я получаю эти два вектора, содержащие процентили.

percentileReal =  c(23.08,23.7,24.16,24.86,25.08,25.08,25.16,25.47,25.90)
percentileTheo =  c(22.50,23.24,23.78,24.23,24.66,25.09,25.54,26.08,26.82)

Теперь я хочу рассчитать доверительный интервал для alpha=0.05 для теоретического процентиля. Если я помню себя правильно, формула дается

error = z*sigma/sqrt(n),
value = +- error

с n=length(data) а также z=quantil of the normal distribution for the given p,

Поэтому, чтобы получить доверительный интервал для 2-го процентиля, я сделаю следующее:

error = (qnorm(20+alpha/2,mu,sigma)-qnorm(20-alpha/2,mu,sigma))*sigma/sqrt(n) 

Вставьте значения:

error = (qnorm(0.225,24.6609,1.6828)-qnorm(0.175,24.6609,1.6828)) * 1.6828/sqrt(11)
error = 0.152985
confidenceInterval(for 2nd percentil) = [23.24+0.152985,23.24-0.152985]
confidenceInterval(for 2nd percentil) = [23.0870,23.3929]

Наконец у меня есть

percentileTheoLower = c(...,23.0870,.....)
percentileTheoUpper = c(...,23.3929,.....)

то же самое для остальных....

Так что вы думаете, я могу пойти с этим?

Answer 1

Если вашей целью является проверка соответствия данных нормальному распределению, используйте тест shapiro.wilk:

shapiro.test(data)
# Shapiro-Wilk normality test
# data:  data
# W = 0.9409, p-value = 0.5306

1-p вероятность того, что распределение ненормально. Итак, с p>0.05 мы не можем утверждать, что распределение ненормально. Грубая интерпретация заключается в том, что "существует 53% вероятности того, что распределение нормальное".

Вы также можете использовать qqplot(...), Чем более линейен этот график, тем больше вероятность того, что ваши данные будут нормально распределены.

 qqnorm(data)

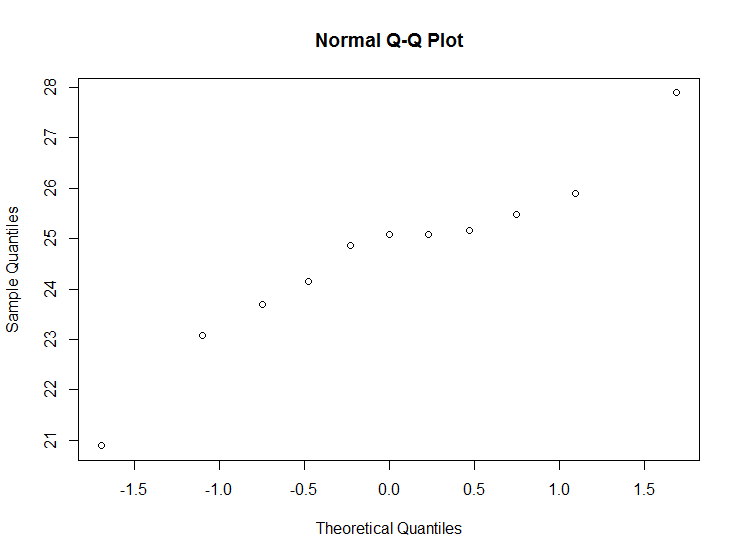
И, наконец, в R есть самый классный пакет, в котором, помимо прочего, есть тест Пирсона Chi-Sq на нормальность:

 library(nortest)
 pearson.test(data)
 #  Pearson chi-square normality test
 #  data:  data
 #  P = 3.7273, p-value = 0.2925

Этот (более консервативный) тест предполагает, что вероятность нормального распределения составляет всего 29%. Все эти тесты полностью объяснены в документации.