Стохастический градиент для глубокого обучения

Question

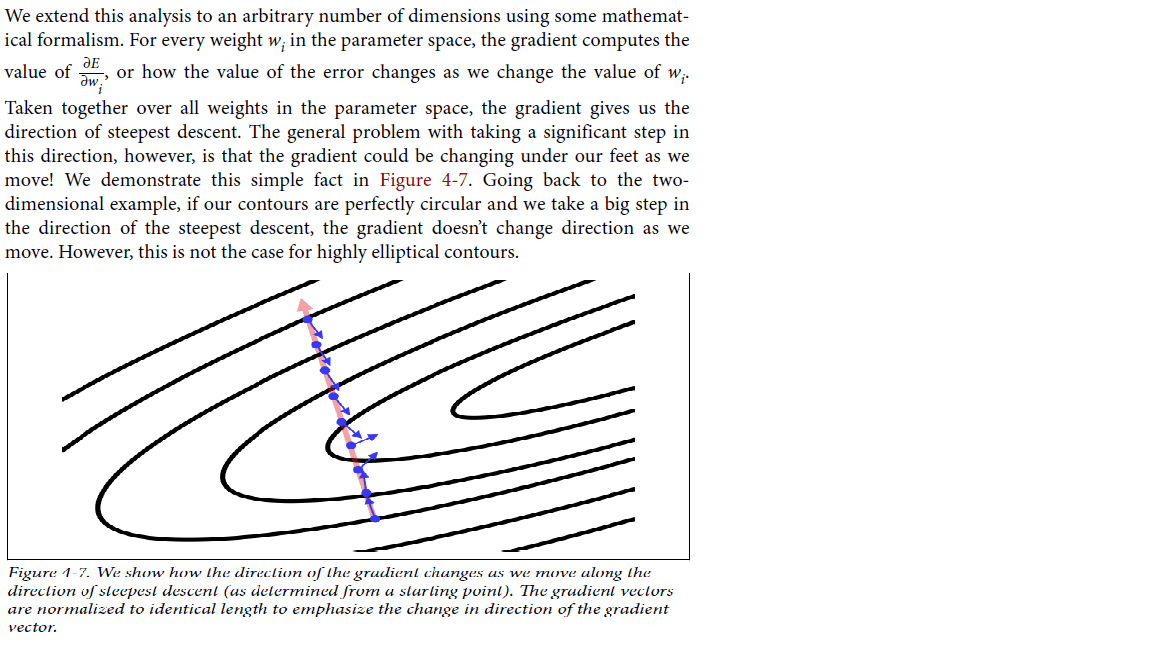
Я читаю о концепции глубокого обучения стохастического градиента. Здесь, на снимке ниже, я не понимаю, что означает утверждение: "Однако общая проблема с существенным шагом в этом направлении заключается в том, что при движении мы можем изменить градиент под нашими ногами!" Мы демонстрируем этот простой факт на следующем рисунке. Я не умею интерпретировать эту цифру. Пожалуйста, объясните

Answer 1

Мы хотим уменьшить погрешность между прогнозируемым значением и фактическим значением. Рассмотрим фактические и прогнозируемые значения как точку в 2D. Вы должны переместить точку прогнозируемого значения как можно ближе к точке фактического значения. Чтобы переместить точку, вам нужно направление, и SGD предоставляет его.

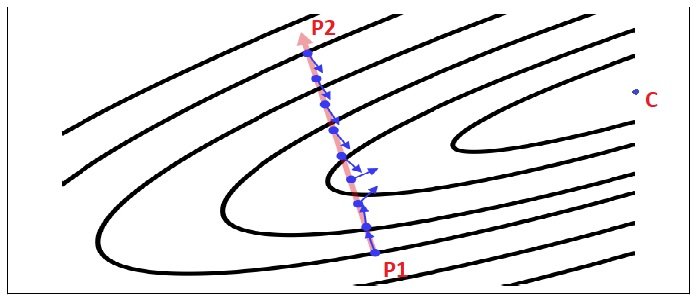
Посмотрите на изображение, C, центр контуров является фактическим значением, а P1 является первым прогнозируемым значением, а SGD (синяя стрелка) показывает направление, которое уменьшает расстояние между P1 и C. Если вы начинаете с P1 и берете значительный (большой) шаг в направлении первой стрелки, вы закончите на P2, который находится далеко от C. Однако, если вы делаете маленькие шаги (синие точки), и на каждом шаге вы двигаетесь, основываясь на новом направлении SGD (синий стрелки в каждой точке) вы попадете в точку, близкую к C.

Большие шаги заставляют вас колебаться вокруг фактического значения, также слишком маленькие шаги занимают слишком много времени, чтобы добраться до фактического значения. Большую часть времени мы используем большие шаги в начале процесса обучения, а затем делаем его маленьким и маленьким.