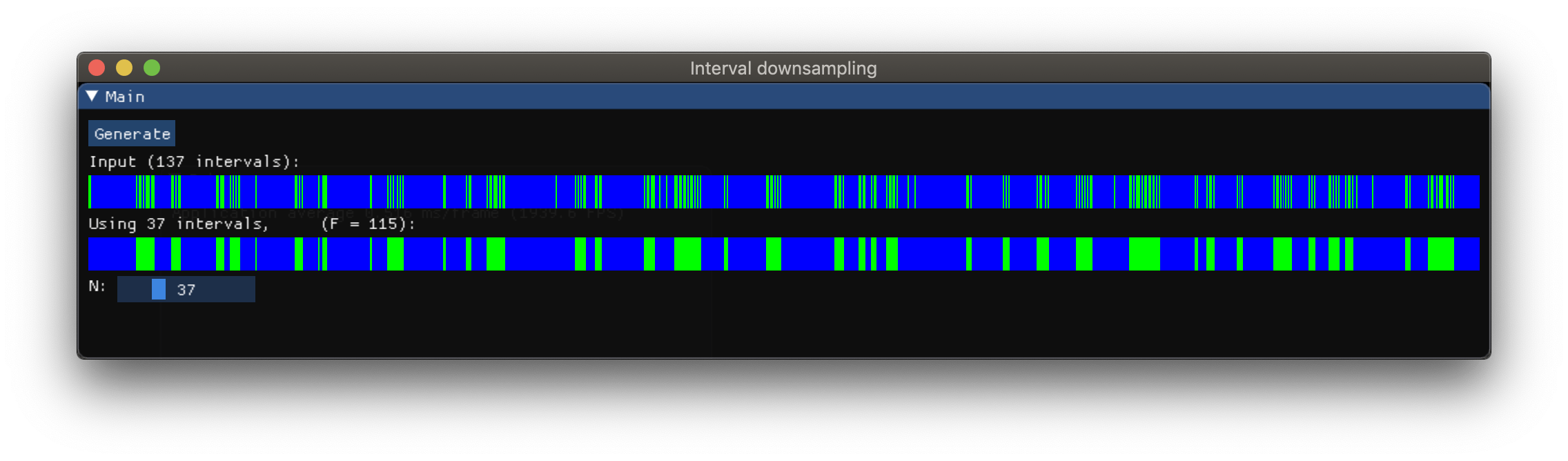
Алгоритм понижающей дискретизации массива интервалов

Question

Алгоритм понижающей дискретизации массива интервалов

У меня есть отсортированный массив из N интервалов разной длины. Я строю эти интервалы с чередующимися цветами синий / зеленый.

Я пытаюсь найти метод или алгоритм, чтобы "уменьшить выборку" массива интервалов, чтобы получить визуально похожий график, но с меньшим количеством элементов.

В идеале я мог бы написать некоторую функцию, в которой я могу передать целевое число выходных интервалов в качестве аргумента. Выходная длина должна приближаться к цели.

input = [
  [0, 5, "blue"],
  [5, 6, "green"],
  [6, 10, "blue"],
  // ...etc
]

output = downsample(input, 25)
// [[0, 10, "blue"], ... ]

Ниже картина того, чего я пытаюсь достичь. В этом примере вход имеет около 250 интервалов, а вывод - около 25 интервалов. Длина ввода может сильно варьироваться.

7

algorithm intervals downsampling

Источник

user980929 30 дек '18 в 14:34

5 ответов

Решение

Я бы предложил использовать K-означает, что это алгоритм, используемый для группировки данных (более подробное объяснение здесь: https://en.wikipedia.org/wiki/K-means_clustering и здесь https://scikit-learn.org/stable/modules/generated/sklearn.cluster.KMeans.html) это было бы кратким объяснением того, как должна выглядеть функция, надеюсь, она будет полезна.

from sklearn.cluster import KMeans
import numpy as np

def downsample(input, cluster = 25):

    # you will need to group your labels in a nmpy array as shown bellow
    # for the sake of example I will take just a random array
    X = np.array([[1, 2], [1, 4], [1, 0],[4, 2], [4, 4], [4, 0]])

    # n_clusters will be the same as desired output
    kmeans = KMeans(n_clusters= cluster, random_state=0).fit(X)

    # then you can iterate through labels that was assigned to every entr of your input
    # in our case the interval
    kmeans_list = [None]*cluster
    for i in range(0, X.shape[0]):
        kmeans_list[kmeans.labels_[i]].append(X[i])

    # after that you will basicly have a list of lists and every inner list will contain all points that corespond to a
    # specific label

    ret = [] #return list
    for label_list in kmeans_list:
        left = 10001000 # a big enough number to exced anything that you will get as an input
        right = -left   # same here
        for entry in label_list:
            left = min(left, entry[0])
            right = max(right, entry[1])
        ret.append([left,right])

    return ret

1

Источник

user8512744 30 дек '18 в 19:16

Вот еще одна попытка динамического программирования, которая немного отличается от попытки Георгия Герганова, хотя идея его попытки сформулировать динамическую программу, возможно, была вдохновлена его ответом. Ни реализация, ни концепция не гарантированы, но я включил набросок кода с наглядным примером:)

В этом случае пространство поиска зависит не от общей ширины блока, а от количества интервалов. Это O(N * n^2) время и O(N * n) пространство, где N а также n являются целью и заданным количеством (зеленых) интервалов, соответственно, потому что мы предполагаем, что любой новый выбранный зеленый интервал должен быть ограничен двумя зелеными интервалами (а не простираться произвольно в фон).

Идея также использует идею суммы префиксов, используемую для расчета прогонов с мажоритарным элементом. Мы добавляем 1, когда видим целевой элемент (в данном случае зеленый) и вычитаем 1 для других (этот алгоритм также поддается нескольким элементам с параллельным отслеживанием суммы префикса). (Я не уверен, что ограничение возможных интервалов для секций с большинством целевого цвета всегда оправдано, но это может быть полезной эвристикой в зависимости от желаемого результата. Она также настраивается - мы можем легко настроить ее для проверки другого часть, чем 1/2.)

Там, где программа Георгия Герганова стремится минимизировать, эта динамическая программа стремится максимизировать два соотношения. Позволять h(i, k) представляют лучшую последовательность зеленых интервалов до i данный интервал, используя k интервалы, где каждому разрешено растягиваться до левого края некоторого предыдущего зеленого интервала. Мы предполагаем, что

h(i, k) = max(r + C*r1 + h(i-l, k-1))

где в текущем интервале кандидатов r отношение зеленого к длине участка, и r1 это отношение зеленого к общему количеству данного зеленого. r1 умножается на регулируемую константу, чтобы придать больший вес объему зеленого цвета. l это длина отрезка.

Код JavaScript (для отладки включает несколько дополнительных переменных и строк журнала):

function rnd(n, d=2){
  let m = Math.pow(10,d)
  return Math.round(m*n) / m;
}

function f(A, N, C){
  let ps = [[0,0]];
  let psBG = [0];
  let totalG = 0;
  A.unshift([0,0]);

  for (let i=1; i<A.length; i++){
    let [l,r,c] = A[i];
    
    if (c == 'g'){
      totalG += r - l;
      let prevI = ps[ps.length-1][1];
      let d = l - A[prevI][1];
      let prevS = ps[ps.length-1][0];
      ps.push(
        [prevS - d, i, 'l'],
        [prevS - d + r - l, i, 'r']
      );
      psBG[i] = psBG[i-1];

    } else {
      psBG[i] = psBG[i-1] + r - l;
    }
  }
  //console.log(JSON.stringify(A));
  //console.log('');
  //console.log(JSON.stringify(ps));
  //console.log('');
  //console.log(JSON.stringify(psBG));

  let m = new Array(N + 1);
  m[0] = new Array((ps.length >> 1) + 1);
  for (let i=0; i<m[0].length; i++)
    m[0][i] = [0,0];

  // for each in N
  for (let i=1; i<=N; i++){
    m[i] = new Array((ps.length >> 1) + 1);
    for (let ii=0; ii<m[0].length; ii++)
      m[i][ii] = [0,0];

    // for each interval
    for (let j=i; j<m[0].length; j++){
      m[i][j] = m[i][j-1];

      for (let k=j; k>i-1; k--){
        // our anchors are the right
        // side of each interval, k's are the left
        let jj = 2*j;
        let kk = 2*k - 1;

        // positive means green
        // is a majority
        if (ps[jj][0] - ps[kk][0] > 0){
          let bg = psBG[ps[jj][1]] - psBG[ps[kk][1]];
          let s = A[ps[jj][1]][1] - A[ps[kk][1]][0] - bg;
          let r = s / (bg + s);
          let r1 = C * s / totalG;
          let candidate = r + r1 + m[i-1][j-1][0];
          
          if (candidate > m[i][j][0]){
            m[i][j] = [
              candidate,
              ps[kk][1] + ',' + ps[jj][1],
              bg, s, r, r1,k,m[i-1][j-1][0]
            ];
          }
        }
      }
    }
  }
  /*
  for (row of m)
    console.log(JSON.stringify(
      row.map(l => l.map(x => typeof x != 'number' ? x : rnd(x)))));
  */
  let result = new Array(N);
  let j = m[0].length - 1;
  for (let i=N; i>0; i--){
    let [_,idxs,w,x,y,z,k] = m[i][j];
    let [l,r] = idxs.split(',');
    result[i-1] = [A[l][0], A[r][1], 'g'];
    j = k - 1;
  }

  return result;
}

function show(A, last){
  if (last[1] != A[A.length-1])
    A.push(last);

  let s = '';
  let j;

  for (let i=A.length-1; i>=0; i--){
    let [l, r, c] = A[i];
    let cc = c == 'g' ? 'X' : '.';
    for (let j=r-1; j>=l; j--)
      s = cc + s;
    if (i > 0)
      for (let j=l-1; j>=A[i-1][1]; j--)
        s = '.' + s
  }

  for (let j=A[0][0]-1; j>=0; j--)
    s = '.' + s

  console.log(s);
  return s;
}

function g(A, N, C){
  const ts = f(A, N, C);
  //console.log(JSON.stringify(ts));
  show(A, A[A.length-1]);
  show(ts, A[A.length-1]);
}


var a = [
  [0,5,'b'],
  [5,9,'g'],
  [9,10,'b'],
  [10,15,'g'],
  [15,40,'b'],
  [40,41,'g'],
  [41,43,'b'],
  [43,44,'g'],
  [44,45,'b'],
  [45,46,'g'],
  [46,55,'b'],
  [55,65,'g'],
  [65,100,'b']
];

// (input, N, C)
g(a, 2, 2);
console.log('');
g(a, 3, 2);
console.log('');
g(a, 4, 2);
console.log('');
g(a, 4, 5);

1

Источник

user2034787 02 янв '19 в 04:56

Вы можете сделать следующее:

Запишите точки, которые делят всю полосу на интервалы как массив [a[0], a[1], a[2], ..., a[n-1]], В вашем примере массив будет [0, 5, 6, 10, ... ],
Рассчитать длину двух интервалов a[2]-a[0], a[3]-a[1], a[4]-a[2], ..., a[n-1]-a[n-3] и найти наименьшее из них. Будь как будет a[k+2]-a[k], Если есть две или более одинаковые длины, имеющие наименьшее значение, выберите одну из них случайным образом. В вашем примере вы должны получить массив [6, 5, ... ] и искать минимальное значение через него.
Поменяйте местами интервалы (a[k], a[k+1]) а также (a[k+1], a[k+2]), В основном вам нужно назначить a[k+1]=a[k]+a[k+2]-a[k+1] чтобы сохранить длину, и удалить точки a[k] а также a[k+2] после этого из массива, потому что две пары интервалов одного цвета теперь объединены в два больших интервала. Таким образом, количество синих и зеленых интервалов уменьшается на один каждый после этого шага.
Если вас устраивает текущее количество интервалов, завершите процесс, в противном случае перейдите к шагу 1.

Вы выполнили шаг 2, чтобы уменьшить "сдвиг цвета", потому что на шаге 3 левый интервал перемещается a[k+2]-a[k+1] вправо и правый интервал перемещается a[k+1]-a[k] налево. Сумма этих расстояний, a[k+2]-a[k] можно считать мерой изменений, которые вы вносите в общую картину.

Основные преимущества этого подхода:

Это просто
Это не дает предпочтения ни одному из двух цветов. Вам не нужно назначать один из цветов для фона, а другой - для рисования. Картинку можно рассматривать как "зеленый на синем" и "синий на зеленом". Это отражает довольно распространенный случай использования, когда два цвета просто описывают два противоположных состояния (например, бит 0/1, "да / нет" ответ) некоторого процесса, распространенного во времени или в пространстве.
Он всегда сохраняет баланс между цветами, т.е. сумма интервалов каждого цвета остается неизменной в процессе уменьшения. Таким образом, общая яркость картинки не меняется. Это важно, поскольку эту общую яркость в некоторых случаях можно считать "индикатором полноты".

1

Источник

user9772691 30 дек '18 в 19:17

Я бы посоветовал вам использовать вейвлет Хаара. Это очень простой алгоритм, который часто использовался для обеспечения функциональности прогрессивной загрузки больших изображений на веб-сайтах.

Здесь вы можете увидеть, как это работает с 2D-функцией. Это то, что вы можете использовать. Увы, документ на украинском языке, но код на C++, так что читабельно:)

Этот документ предоставляет пример трехмерного объекта:

Псевдокод о том, как сжимать с помощью вейвлета Хаара, вы можете найти в Вейвлетах для компьютерной графики: Учебник для начинающих, часть 1y.

1

Источник

user312896 30 дек '18 в 19:33

Другие вопросы по тегам algorithm intervals downsampling

user4039976 30 дек '18 в 22:00 2018-12-30 22:00 · Accepted Answer · 2018-12-30 22:00

Обновление 1:

Ниже мой оригинальный пост, который я первоначально удалил, потому что были проблемы с отображением уравнений, а также я не был уверен, действительно ли это имеет смысл. Но позже я решил, что описанная мною проблема оптимизации может быть эффективно решена с помощью DP (динамического программирования).

Итак, я сделал пример реализации C++. Вот некоторые результаты:

Gif

Вот живая демонстрация, с которой вы можете играть в своем браузере (убедитесь, что браузер поддерживает WebGL2, например, Chrome или Firefox). Загрузка страницы занимает немного времени.

Вот реализация C++: ссылка

Обновление 2:

Оказывается, предлагаемое решение обладает следующим приятным свойством - мы можем легко контролировать важность двух частей F ₁ и F ₂ функции стоимости. Просто измените функцию стоимости на F (α) = F ₁ + αF ₂, где α > = 1.0 - свободный параметр. Алгоритм DP остается прежним.

Вот некоторые результаты для разных значений α, использующих одинаковое количество интервалов N:

Демонстрационная версия ^{(требуется WebGL2)}

Как можно видеть, более высокое значение α означает, что более важно охватить исходные интервалы ввода, даже если это означает охват большего количества промежуточного фона.

Оригинальный пост

Несмотря на то, что некоторые хорошие алгоритмы уже были предложены, я хотел бы предложить немного необычный подход - интерпретировать задачу как задачу оптимизации. Хотя я не знаю, как эффективно решить проблему оптимизации (или даже если она вообще может быть решена в разумные сроки), она может быть полезна кому-то исключительно как концепция.

Во-первых, без потери общности, давайте объявим синий цвет фоном. Мы будем рисовать N зеленых интервалов поверх него (N - это число, предоставленное downsample() функция в описании ОП). I- ^й интервал определяется его начальной координатой 0 <= x _i max

и шириной w _i > = 0 (x _max - максимальная координата от входа).

Давайте также определим массив G(x) как число зеленых ячеек в интервале [0, x) во входных данных. Этот массив может быть легко рассчитан заранее. Мы будем использовать его для быстрого вычисления количества зеленых клеток в произвольном интервале [x, y), а именно: G (y) - G(x).

Теперь мы можем ввести первую часть функции стоимости для нашей задачи оптимизации:

Чем меньше F ₁, тем лучше наши сгенерированные интервалы покрывают входные интервалы, поэтому мы будем искать x _i, w _i, которые минимизируют его. В идеале мы хотим, чтобы F ₁ = 0, что означало бы, что интервалы не покрывают какой-либо фон (что, конечно, невозможно, поскольку N меньше входных интервалов).

Однако этой функции недостаточно для описания проблемы, поскольку, очевидно, мы можем минимизировать ее, используя пустые интервалы: F ₁ (x, 0) = 0. Вместо этого мы хотим охватить как можно больше из интервалов ввода. Давайте введем вторую часть функции стоимости, которая соответствует этому требованию:

Чем меньше F ₂, тем больше входных интервалов покрыто. В идеале мы хотим, чтобы F ₂ = 0, что означало бы, что мы покрыли все входные прямоугольники. Однако минимизация F ₂ конкурирует с минимизацией F ₁.

Наконец, мы можем сформулировать нашу задачу оптимизации: найти x _i, w _i, которые минимизируют F = F ₁ + F ₂

Как решить эту проблему? Точно сказать не могу. Может быть, использовать метаэвристический подход для глобальной оптимизации, такой как имитация отжига или дифференциальная эволюция. Как правило, их легко реализовать, особенно для этой простой функции стоимости.

В лучшем случае существовал бы некий алгоритм DP для его эффективного решения, но вряд ли.