Нахождение пересечения двух окружностей
Я пытаюсь найти пересечения между двумя кругами в Python(используя Matplotlib), но не могу получить какие-либо значения обратно.
Я делаю это, создавая списки X и Y для каждого отдельного круга (Matplotlib принимает первый аргумент как значения X, а второй - как значения Y при рисовании круга), а затем пересекает списки соответственно (например, circle1 x values со значениями circle2 x).
import numpy
import math
import matplotlib.pyplot as plt
import random
def origin_circle():
global x_points
global y_points
global r
global n
r=1
n=2**16
x_points=[(r*math.cos(t)) for t in numpy.linspace(0, 2*numpy.pi*r, n+1)]
y_points=[(r*math.sin(t)) for t in numpy.linspace(0, 2*numpy.pi*r, n+1)]
def new_circle(x_offset, y_offset):
global x_points1
global y_points1
x_points1=[x_offset+(r*math.cos(t)) for t in numpy.linspace(0, 2*numpy.pi*r, n+1)]
y_points1=[y_offset+(r*math.sin(t)) for t in numpy.linspace(0, 2*numpy.pi*r, n+1)]
origin_circle()
new_center= random.randint(0, len(x_points))
x_offset = x_points[new_center]
y_offset = y_points[new_center]
new_circle(x_offset, y_offset)
print(set(x_points1).intersection(set(x_points)))
print(set(y_points1).intersection(set(y_points)))
Я ожидал получить значения обратно, но набор, который вернулся, был пустым.
PS: Надеюсь, этот вопрос написан плохо, возможно, это мой последний вопрос на этом сайте из-за этого D:
5 ответов
Правильный метод решения для точек пересечения двух окружностей алгебраически. Вы не можете сделать это, используя точки (координаты x, y) из-за бесконечной точности системы координат (действительные числа).
Если два круга пересекаются в двух точках, то существует прямой способ вычисления этих двух точек пересечения. Алгебра подробно здесь в разделе Intersection of two circles,
Мы также можем исключить случаи, когда два круга не пересекаются, как показано ниже
- Если расстояние между двумя источниками окружности> сумма радиусов двух окружностей, то это означает, что окружность отделена и поэтому не пересекается.
- Если расстояние между двумя началами окружности <абсолютная разница между радиусами двух окружностей, то это означает, что один круг содержится в другом и поэтому не пересекается.
Код для возврата двух пересекающихся точек двух окружностей. Каждый крикл описывается своим центром (x,y) и радиусом (r)
def get_intercetions(x0, y0, r0, x1, y1, r1):
# circle 1: (x0, y0), radius r0
# circle 2: (x1, y1), radius r1
d=math.sqrt((x1-x0)**2 + (y1-y0)**2)
# non intersecting
if d > r0 + r1 :
return None
# One circle within other
if d < abs(r0-r1):
return None
# coincident circles
if d == 0 and r0 == r1:
return None
else:
a=(r0**2-r1**2+d**2)/(2*d)
h=math.sqrt(r0**2-a**2)
x2=x0+a*(x1-x0)/d
y2=y0+a*(y1-y0)/d
x3=x2+h*(y1-y0)/d
y3=y2-h*(x1-x0)/d
x4=x2-h*(y1-y0)/d
y4=y2+h*(x1-x0)/d
return (x3, y3, x4, y4)
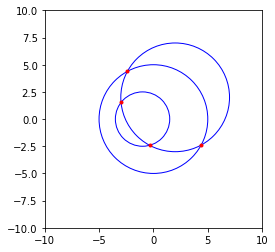
Давайте проверим это (визуально), построив график
# intersection circles
x0, y0 = 0, 0
r0 = 5
x1, y1 = 2, 2
r1 = 5
# intersecting with (x1, y1) but not with (x0, y0)
x2, y2 = -1,0
r2 = 2.5
circle1 = plt.Circle((x0, y0), r0, color='b', fill=False)
circle2 = plt.Circle((x1, y1), r1, color='b', fill=False)
circle3 = plt.Circle((x2, y2), r2, color='b', fill=False)
fig, ax = plt.subplots()
ax.set_xlim((-10, 10))
ax.set_ylim((-10, 10))
ax.add_artist(circle1)
ax.add_artist(circle2)
ax.add_artist(circle3)
intersections = get_intercetions(x0, y0, r0, x1, y1, r1)
if intersections is not None:
i_x3, i_y3, i_x4, i_y4 = intersections
plt.plot([i_x3, i_x4], [i_y3, i_y4], '.', color='r')
intersections = get_intercetions(x0, y0, r0, x2, y2, r2)
if intersections is not None:
i_x3, i_y3, i_x4, i_y4 = intersections
plt.plot([i_x3, i_x4], [i_y3, i_y4], '.', color='r')
intersections = get_intercetions(x1, y1, r1, x2, y2, r2)
if intersections is not None:
i_x3, i_y3, i_x4, i_y4 = intersections
plt.plot([i_x3, i_x4], [i_y3, i_y4], '.', color='r')
plt.gca().set_aspect('equal', adjustable='box')
Выход:
Если вы работаете с кругами, правильный подход для получения пересечений заключается в использовании некоторой алгебры. Существует четыре возможных случая: отсутствие пересечения, одно пересечение (касание), два пересечения и бесконечное пересечение (это один и тот же круг). Давайте сосредоточимся на случае двух пересечений.
Из /questions/44571524/kak-vyi-balansiruete-frameworkapi-design-i-tdd/44571548#44571548 вы можете получить линейное уравнение, связывающее x с y вдоль линии, проходящей через две точки пересечения:
−2x(x1center−x2center)−2y(y1center−y2center) = (r1)^2−(r2)^2−((x1center)^2−(x2center)^2)−((y1center)^2−(y2center)^2).
Отсюда вы получаете формулу для y в терминах x, а затем подставляете y в одну из формул своего круга, чтобы получить квадратичную для x. Если вы не хотите реализовывать решатель квадратичных уравнений, вы можете использовать numpy.roots следующим образом:
root_array = np.roots(quadratic_coeff, linear_coeff, constant_coef)
Посмотрите на то, что вы создали:
new_center= random.randint(0, len(x_points))
x_offset = x_points[new_center]
y_offset = y_points[new_center]
new_circle(x_offset, y_offset)
# I'm sorting these for easier visualization
print(sorted(x_points))
print(sorted(x_points1))
Выход:
[-1.0, -0.9807852804032304, -0.9807852804032304, -0.9238795325112868,
-0.9238795325112867, -0.8314696123025455, -0.8314696123025453, -0.7071067811865477,
-0.7071067811865475, -0.5555702330196022, -0.555570233019602, -0.38268343236509034,
-0.3826834323650897, -0.19509032201612866, -0.1950903220161282,
-1.8369701987210297e-16, 6.123233995736766e-17, 0.1950903220161283,
0.19509032201612833, 0.38268343236508984, 0.38268343236509, 0.5555702330196018
, 0.5555702330196023, 0.7071067811865474, 0.7071067811865476, 0.8314696123025452,
0.8314696123025452, 0.9238795325112865, 0.9238795325112867, 0.9807852804032303,
0.9807852804032304, 1.0, 1.0]
[-2.0, -1.9807852804032304, -1.9807852804032304, -1.923879532511287,
-1.9238795325112867, -1.8314696123025453, -1.8314696123025453, -1.7071067811865477,
-1.7071067811865475, -1.5555702330196022, -1.555570233019602, -1.3826834323650903,
-1.3826834323650896, -1.1950903220161286, -1.1950903220161282, -1.0000000000000002,
-0.9999999999999999, -0.8049096779838717, -0.8049096779838717, -0.6173165676349102,
-0.6173165676349099, -0.44442976698039816, -0.4444297669803977, -0.29289321881345265,
-0.2928932188134524, -0.16853038769745476, -0.16853038769745476,
-0.07612046748871348, -0.07612046748871326, -0.01921471959676968,
-0.01921471959676957, 0.0, 0.0]
Прежде всего, вы создали независимые списки координат; у вас нет очков как согласованной пары любого вида.
Во-вторых, вы не перечислили все точки на окружности: вы не можете, так как это бесконечное множество. Вместо этого вы сгенерировали список (ну, по одному для каждого x а также y) одинакового расстояния Нет математической причины ожидать, что у вас будет точное совпадение между любыми двумя такими координатами, не говоря уже о том, чтобы выбрать две точки на каждом круге, которые являются точками пересечения.
Вы ничего не получите обратно, потому что ваши списки не имеют общих точек. Если вы хотите найти точки пересечения, вам нужно сделать это с помощью алгебраического решения, последовательного приближения или другого метода. Например, возьмите разницу двух окружностей и решите это уравнение для y == 0,
Приведенный выше код построения точек пересечения не отображал точки пересечения должным образом. Я скорректировал код, чтобы отобразить их следующим образом:
import matplotlib.pyplot as plt
import math
def get_intersections(x0, y0, r0, x1, y1, r1):
# circle 1: (x0, y0), radius r0
# circle 2: (x1, y1), radius r1
d=math.sqrt((x1-x0)**2 + (y1-y0)**2)
# non intersecting
if d > r0 + r1 :
return {}
# One circle within other
if d < abs(r0-r1):
return {}
# coincident circles
if d == 0 and r0 == r1:
return {}
else:
a=(r0**2-r1**2+d**2)/(2*d)
h=math.sqrt(r0**2-a**2)
x2=x0+a*(x1-x0)/d
y2=y0+a*(y1-y0)/d
x3=x2+h*(y1-y0)/d
y3=y2-h*(x1-x0)/d
x4=x2-h*(y1-y0)/d
y4=y2+h*(x1-x0)/d
return x3, y3, x4, y4
# intersection circles
x0, y0 = 0, 0
r0 = 5
x1, y1 = 2, 2
r1 = 5
# intersecting with (x1, y1) but not with (x0, y0)
x2, y2 = -1,0
r2 = 2.5
circle1 = plt.Circle((x0, y0), r0, color='b', fill=False)
circle2 = plt.Circle((x1, y1), r1, color='b', fill=False)
circle3 = plt.Circle((x2, y2), r2, color='b', fill=False)
fig = plt.figure(figsize = (10, 10))
plt.grid(True)
ax = fig.add_subplot(111)
ax.set_xlim((-10, 10))
ax.set_ylim((-10, 10))
ax.add_artist(circle1)
ax.add_artist(circle2)
ax.add_artist(circle3)
intersections1 = get_intersections(x0, y0, r0, x1, y1, r1)
print(intersections1)
if len(intersections1) > 0:
print(intersections3)
i_x3, i_y3, i_x4, i_y4 = intersections1
#plt.plot([i_x3, i_x4], [i_y3, i_y4], 'o', color='r')
ax.scatter([i_x3, i_x4],[i_y3, i_y4] ,marker ='X',s=300,alpha=1)
intersections2 = get_intersections(x0, y0, r0, x2, y2, r2)
print(intersections2)
if len(intersections2) > 0:
i_x3, i_y3, i_x4, i_y4 = intersections2
plt.plot([i_x3, i_x4], [i_y3, i_y4], 'o', color='r')
ax.scatter([i_x3, i_x4],[i_y3, i_y4] ,marker ='X',s=300,alpha=1)
intersections3 = get_intersections(x1, y1, r1, x2, y2, r2)
if len(intersections3) > 0:
print(intersections3)
i_x3, i_y3, i_x4, i_y4 = intersections3
#plt.plot([i_x3, i_x4], [i_y3, i_y4], 'o', color='r')
ax.scatter([i_x3, i_x4],[i_y3, i_y4] ,marker ='X',s=300,alpha=1)
plt.gca().set_aspect('equal', adjustable='box')
Результат представлен на картинке:
Неправильный язык для математики / геометрии. Вот как это выглядит на более подходящем языке (WL)
Circle @@@ Thread @ {RandomReal[{-1,1},{3,2}], RandomReal[{.5,1},3]} //
Graphics[{
#, Red,
RegionIntersection @@@ #~Subsets~{2}
}]&