Как рассчитать оптимальное распределение частот слов в тексте по zipf

Question

Для выполнения домашнего задания я должен нанести частоту слов текста и сравнить ее с оптимальной zipf распределение.

Построение подсчитанных частот слов текста в соответствии с их рангом в журнале журнала, кажется, работает нормально.

Но я спорю с расчетом оптимального распределения zipf. Результат должен выглядеть примерно так:

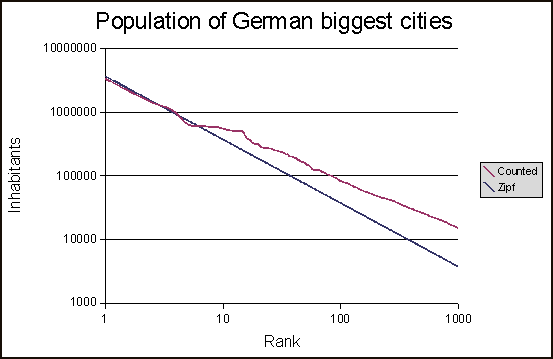
Я не понимаю, как будет выглядеть уравнение для расчета прямой zipf линия.

На немецкой странице Википедии zipf закон я нашел уравнение, которое, кажется, работает

но источники не приводятся, поэтому я не понимаю, где постоянная 1.78 происходит от.

#tokenizes the file 
tokens = word_tokenize(raw)
tokensNLTK = Text(tokens)

#calculates the FreqDist of all words - all words in lower case
freq_list = FreqDist([w.lower() for w in tokensNLTK]).most_common()

#Data for X- and Y-Axis plot
values=[]
for item in (freq_list):
    value = (list(item)[1]) / len([w.lower() for w in tokensNLTK])
    values.append(value)

#graph of counted frequencies gets plotted
plt.yscale('log')
plt.xscale('log')
plt.plot(np.array(list(range(1, (len(values)+1)))), np.array(values))

#graph of optimal zipf distribution is plotted
optimal_zipf = 1/(np.array(list(range(1, (len(values)+1))))* np.log(1.78*len(values)))###1.78
plt.plot(np.array(list(range(1, (len(values)+1)))), optimal_zipf)
plt.show()

Мои результаты с этим скриптом выглядят так:

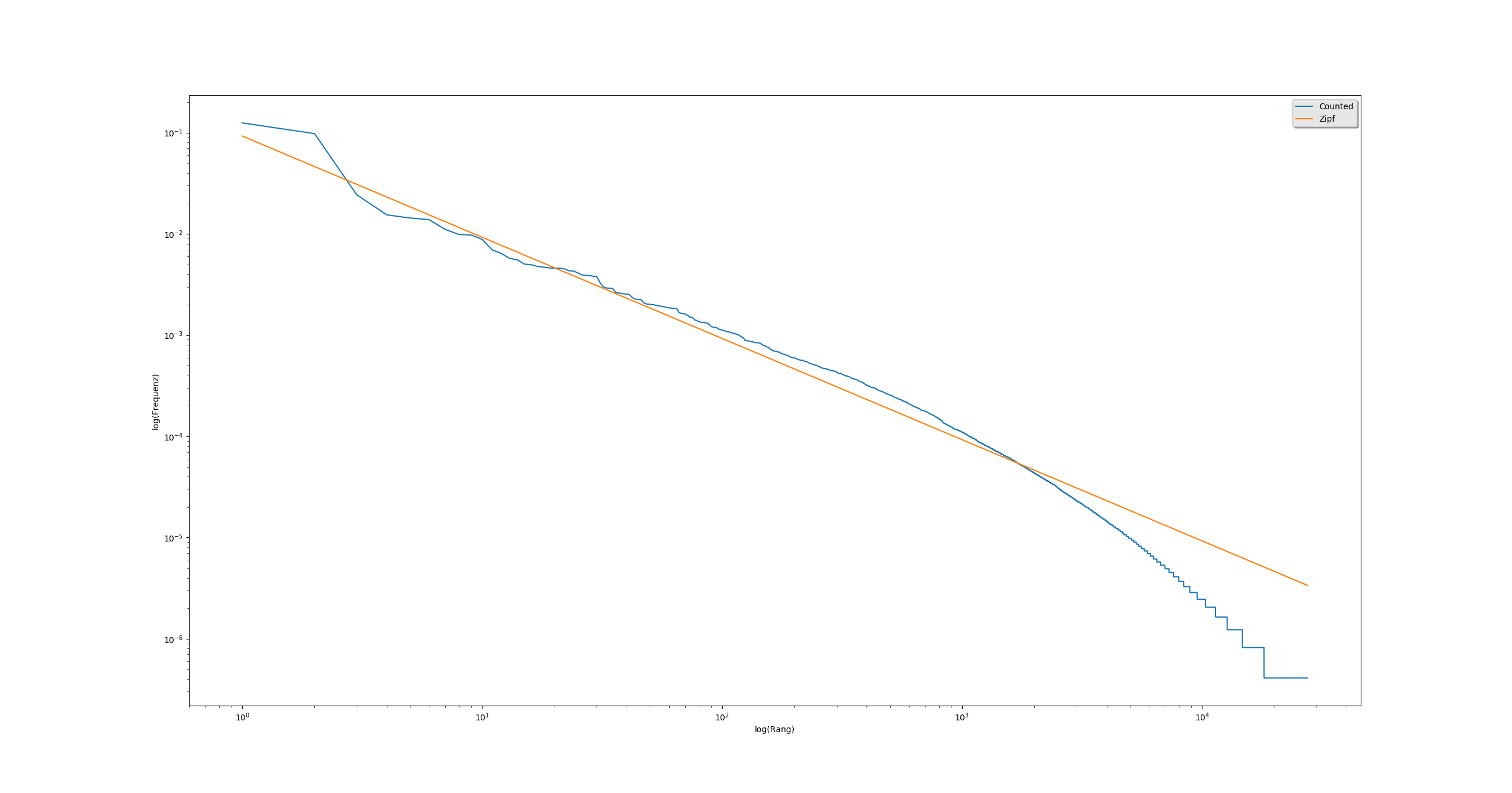
но я просто не уверен, что оптимальный zipf Распределение рассчитывается правильно. Если это так, не должно быть оптимальным zipf Распределение пересекает ось X в одной точке?

РЕДАКТИРОВАТЬ: если это поможет, мой текст имеет 2440400 токенов и 27491 типов

Answer 1

Взгляните на эту исследовательскую работу Эндрю Уильяма Чисхолма. В частности, страница № 22.

H (N) ≈ ln (N) + γ

Где γ - постоянная Эйлера-Маскерони с приблизительным значением 0,57721. Отмечая, что exp(γ) ≈ 1,78, уравнение <...> можно переписать так, чтобы оно стало для больших N (N должно быть больше 1000, чтобы это было с точностью до одной части из тысячи).

pr ≈ 1 / [r * ln (1,78*N)]