Советы по созданию диаграмм Графа

Question

Я хотел бы программно создавать диаграммы, подобные этой http://yaroslavvb.com/upload/junction-tree-decomposition.png

Я полагаю, что я должен использовать GraphPlot с VertexCoordinateRules, VertexRenderingFunction и EdgeRenderingFunction для графиков. Что я должен использовать для цветных скошенных фонов?

Править Используя в основном идеи Саймона, вот упрощенная "менее надежная" версия, которую я в итоге использовал

Потребности ["GraphUtilities`"];
GraphPlotHighlight[dge_, verts_, color_]:= Module[{},
  vpos = Position[VertexList[edge], Альтернативы @@ verts];
  координаты = Извлечь [GraphCoordinates[ребра], впос];
  (* добавить.002, потому что заглушка исчезает, когда сегменты почти коллинеарны *)  
  AppendTo[координаты, первые [координаты] + .002];
  Show[Graphics[{color, CapForm["Round"], JoinForm["Round"], 
     Толщина [.2], Линия [координаты], Многоугольник [координаты]}],
   GraphPlot[edge], ImageSize -> 150]
  ]

SetOptions[GraphPlot, 
  VertexRenderingFunction -> ({Белый, EdgeForm[Черный], Диск [#, .15], 
      Черный, Текст [#2, #1]} &), 
  EdgeRenderingFunction -> ({Black, Line[#]} &)];
edge = GraphData[{"Grid", {3, 3}}, "EdgeRules"];
colors = {LightBlue, LightGreen, LightRed, LightMagenta};
vsets = {{8, 5, 2}, {7, 5, 8}, {9, 6, 3}, {8, 1, 2}};
MapThread[GraphPlotHighlight[края, # 1, # 2] &, {vsets, colors}]

http://yaroslavvb.com/upload/mathematica-graphs.png

Answer 1

Обобщая ответ Самсдрама немного, я получаю

GraphPlotHighlight[edges:{((_->_)|{_->_,_})..},hl:{___}:{},opts:OptionsPattern[]]:=Module[{verts,coords,g,sub},
  verts=Flatten[edges/.Rule->List]//.{a___,b_,c___,b_,d___}:>{a,b,c,d};
  g=GraphPlot[edges,FilterRules[{opts}, Options[GraphPlot]]];
  coords=VertexCoordinateRules/.Cases[g,HoldPattern[VertexCoordinateRules->_],2];
  sub=Flatten[Position[verts,_?(MemberQ[hl,#]&)]];
  coords=coords[[sub]];     
  Show[Graphics[{OptionValue[HighlightColor],CapForm["Round"],JoinForm["Round"],Thickness[OptionValue[HighlightThickness]],Line[AppendTo[coords,First[coords]]],Polygon[coords]}],g]
]
Protect[HighlightColor,HighlightThickness];
Options[GraphPlotHighlight]=Join[Options[GraphPlot],{HighlightColor->LightBlue,HighlightThickness->.15}];

Часть приведенного выше кода может быть немного более устойчивой, но это работает:

GraphPlotHighlight[{b->c,a->b,c->a,e->c},{b,c,e},VertexLabeling->True,HighlightColor->LightRed,HighlightThickness->.1,VertexRenderingFunction -> ({White, EdgeForm[Black], Disk[#, .06], 
Black, Text[#2, #1]} &)]

---

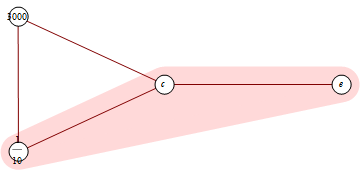
РЕДАКТИРОВАТЬ #1: очищенную версию этого кода можно найти на http://gist.github.com/663438

РЕДАКТИРОВАТЬ № 2: Как обсуждалось в комментариях ниже, шаблон, который мой edges must match - список правил ребер с необязательными метками. Это немного менее общее, чем то, что используется GraphPlot функция (и в соответствии с версией, приведенной выше), где правила границ также могут быть обернуты в Tooltip,

Чтобы найти точный шаблон, используемый GraphPlot Я неоднократно использовал Unprotect[fn];ClearAttributes[fn,ReadProtected];Information[fn] где fn является объектом интереса, пока я не обнаружил, что он использовал следующую (очищенную) функцию:

Network`GraphPlot`RuleListGraphQ[x_] := 
  ListQ[x] && Length[x] > 0 && 
    And@@Map[Head[#1] === Rule 
         || (ListQ[#1] && Length[#1] == 2 && Head[#1[[1]]] === Rule) 
         || (Head[#1] === Tooltip && Length[#1] == 2 && Head[#1[[1]]] === Rule)&, 
      x, {1}]

Я думаю, что мой edges:{((_ -> _) | (List|Tooltip)[_ -> _, _])..} картина эквивалентна и более лаконична...

Answer 2

Для простых примеров, когда вы соединяете только два узла (как ваш пример справа), вы можете нарисовать линии с ограниченными конечными точками, как это.

vertices = {a, b};
Coordinates = {{0, 0}, {1, 1}};
GraphPlot[{a -> b}, VertexLabeling -> True, 
 VertexCoordinateRules -> 
  MapThread[#1 -> #2 &, {vertices, Coordinates}], 
 Prolog -> {Blue, CapForm["Round"], Thickness[.1], Line[Coordinates]}]

Для более сложных примеров (например, второй справа) я бы порекомендовал нарисовать многоугольник, используя координаты вершины, а затем обведя границу многоугольника с помощью ограниченной линии. Я не мог найти способ добавить скошенный край непосредственно к многоугольнику. При трассировке периметра многоугольника необходимо добавить координату первой вершины к концу отрезка, чтобы линия составляла полный периметр многоугольника. Кроме того, есть две отдельные графические директивы для линий CapForm, которые определяют, следует ли наклонять концы линии, и JoinForm, которая указывает, следует ли наклонять промежуточные точки линии.

vertices = {a, b, c};
Coordinates = {{0, 0}, {1, 1}, {1, -1}};
GraphPlot[{a -> b, b -> c, c -> a}, VertexLabeling -> True, 
 VertexCoordinateRules -> 
  MapThread[#1 -> #2 &, {vertices, Coordinates}], 
 Prolog -> {Blue, CapForm["Round"], JoinForm["Round"], Thickness[.15],
    Line[AppendTo[Coordinates, First[Coordinates]]], 
   Polygon[Coordinates]}]

Answer 3

JoinForm["Round"] будет округлять объединения отрезков.

Вам понадобится заполненный многоугольник вокруг центров вершин в цветной области, а затем JoinForm["Round"], ..., Line[{...}] чтобы получить закругленные углы.

Рассматривать

foo = GraphPlot[{a -> b, a -> c, b -> d, b -> e, b -> f, c -> e, e -> f}, 
    VertexRenderingFunction -> 
    ({Белый, EdgeForm[Черный], Диск [#, .1], Черный, Текст [#2, #1]} &)]
Шоу[
    Графика[{
      RGBColor[0,6, 0,8, 1, 1],
      Polygon[foo[[1, 1, 1, 1, 1, {2, 5, 6, 2}]]],
      JoinForm["Round"], толщина [0,2],
      Строка [foo[[1, 1, 1, 1, 1, {2, 5, 6, 2}]]]
    }],
    Foo
]

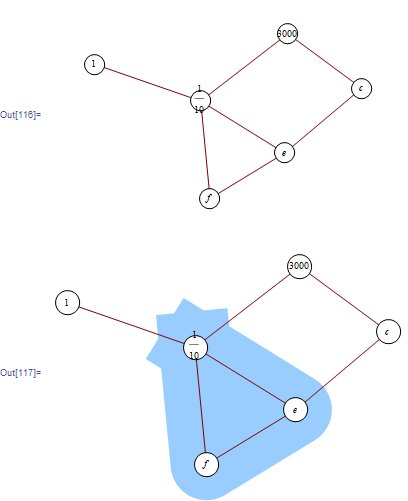
где foo [[1,1,1,1,1]] - список центров вершин, а {2,5,6} извлекает {b, e, f} вершин. ({2,5,6,2} закрывает строку в исходной точке.)

Есть много места для претификации, но я думаю, что это покрывает ингредиент, который вы не упомянули выше.