Создание графика в plot_surface - невозможно правильно преобразовать данные в требуемый формат
У меня возникают проблемы при попытке получить поверхностный график моего массива данных. (См. Ниже для небольшого образца данных испытаний).
Вот мой основной код, который я использую для тестирования различных методов, с которыми я сталкивался.
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
data = np.loadtxt('lobe1.dat')
xs = data[:,0]
ys = data[:,1]
zs = data[:,2]
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(xs,ys,zs, rstride=1, cstride=1,color='b')
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')
ax.set_xlim([-0.08,0.08])
ax.set_ylim([-0.08,0.08])
ax.set_zlim([-0.08,0.08])
ax.set_aspect("equal")
plt.show()
В этой версии я получаю ось графика, но данные отсутствуют. Я сузил это до того факта, что xs, ys, zs должны быть двухмерные массивы. я могу использовать np.meshgrid преобразовать xs, ys но что мне делать с zs? то есть:
xs,ys = np.meshgrid(xs, ys)
zs = ???
Я также натолкнулся на решение, которое предлагает использовать приведенный ниже код и построить новые X, Y, Z (возможно, с некоторой сортировкой массива), но это вызывает
ValueError: total size of new array must be unchanged
по вызову xs.reshape(),
cols = np.unique(xs).shape[0]
X = xs.reshape(-1, cols)
Y = ys.reshape(-1, cols)
Z = zs.reshape(-1, cols)
Это поставило меня в тупик, поэтому я был бы признателен за любой вклад. Обычно я имею дело со значительно большим набором данных, но вот некоторые примеры данных из lobe1.dat чтобы позволить вам повторить мои проблемы. Каждый столбец состоит из xs, ys а также zs соответственно.
0.000000000000000 0.000000000000000 -0.049815118005748
0.039186360495468 0.000000000000000 -0.038410316117142
0.056803651667469 0.000000000000000 -0.024791146049150
0.072097497329379 0.000000000000000 -0.007246071120158
0.067060501396178 0.000000000000000 0.013688667526320
0.051379603016815 0.000000000000000 0.029664027632614
0.031789354260577 0.000000000000000 0.042385805680769
0.000000000000000 0.000000000000000 -0.049815118005748
0.033152869816836 0.019140818313159 -0.037523509346281
0.045829649529645 0.026459760492807 -0.023095972443560
0.052288905121942 0.030189013447784 -0.006068220024078
0.050910857853398 0.029393397486334 0.011999804274721
0.042289602909023 0.024415913623447 0.028193068606016
0.027154245218747 0.015677510786684 0.041806695431158
0.000000000000000 0.000000000000000 -0.049815118005748
0.018422854617625 0.031909320218181 -0.036116018976805
0.024307976693871 0.042102650662984 -0.021217741560168
0.026764953958725 0.046358260118753 -0.005379958170438
0.026279549165091 0.045517514353942 0.010728581020809
0.022786184948649 0.039466830041721 0.026311220027814
0.015304154209252 0.026507572657293 0.040811077891338
0.000000000000000 0.000000000000000 -0.049815118005748
0.000000000000000 0.036309017710339 -0.035589956059286
0.000000000000000 0.047273292454049 -0.020631756287663
0.000000000000000 0.051675786366447 -0.005193611943154
0.000000000000000 0.050815730690458 0.010372717591526
0.000000000000000 0.044489633172666 0.025686101688387
0.000000000000000 0.030316588229639 0.040422117639519
-0.000000000000000 0.000000000000000 -0.049815118005748
-0.018496134334071 0.032036244410230 -0.036259675955309
-0.024429654459698 0.042313402735548 -0.021323950621558
-0.026908703737555 0.046607242039264 -0.005408852963170
-0.026418888079279 0.045758856432786 0.010785465894322
-0.022894621383867 0.039654647456911 0.026436431637941
-0.015355646960057 0.026596760717909 0.040948391893486
-0.000000000000000 0.000000000000000 -0.049815118005748
-0.033286051232919 0.019217710639585 -0.037674248456914
-0.045779044607711 0.026430543727506 -0.023070469960026
-0.051867788406975 0.029945881599038 -0.006019348683662
-0.050596024278383 0.029211628237049 0.011925597289441
-0.042339044284962 0.024444458615154 0.028226029523308
-0.027273140887785 0.015746155233209 0.041989747288558
-0.000000000000000 0.000000000000000 -0.049815118005748
-0.039273413070914 0.000000000000000 -0.038495644708504
-0.055872341877765 0.000000000000000 -0.024384689134220
-0.065935779675748 0.000000000000000 -0.006626795195273
-0.063568190701275 0.000000000000000 0.012975802590838
-0.051006846275802 0.000000000000000 0.029448816427848
-0.031916472879064 0.000000000000000 0.042555297172085
-0.000000000000000 -0.000000000000000 -0.049815118005748
-0.033286051232919 -0.019217710639585 -0.037674248456914
-0.045779044607711 -0.026430543727506 -0.023070469960026
-0.051867788406975 -0.029945881599038 -0.006019348683662
-0.050596024278383 -0.029211628237049 0.011925597289441
-0.042339044284962 -0.024444458615154 0.028226029523308
-0.027273140887785 -0.015746155233209 0.041989747288558
-0.000000000000000 -0.000000000000000 -0.049815118005748
-0.018496134334071 -0.032036244410230 -0.036259675955309
-0.024429654459698 -0.042313402735548 -0.021323950621558
-0.026908703737555 -0.046607242039264 -0.005408852963170
-0.026418888079279 -0.045758856432786 0.010785465894322
-0.022894621383867 -0.039654647456911 0.026436431637941
-0.015355646960057 -0.026596760717909 0.040948391893486
-0.000000000000000 -0.000000000000000 -0.049815118005748
-0.000000000000000 -0.036309017710339 -0.035589956059286
-0.000000000000000 -0.047273292454049 -0.020631756287663
-0.000000000000000 -0.051675786366447 -0.005193611943154
-0.000000000000000 -0.050815730690458 0.010372717591526
-0.000000000000000 -0.044489633172666 0.025686101688387
-0.000000000000000 -0.030316588229639 0.040422117639519
0.000000000000000 -0.000000000000000 -0.049815118005748
0.018422854617625 -0.031909320218181 -0.036116018976805
0.024307976693871 -0.042102650662984 -0.021217741560168
0.026764953958725 -0.046358260118753 -0.005379958170438
0.026279549165091 -0.045517514353942 0.010728581020809
0.022786184948649 -0.039466830041721 0.026311220027814
0.015304154209252 -0.026507572657293 0.040811077891338
0.000000000000000 -0.000000000000000 -0.049815118005748
0.033152869816836 -0.019140818313159 -0.037523509346281
0.045829649529645 -0.026459760492807 -0.023095972443560
0.052288905121942 -0.030189013447784 -0.006068220024078
0.050910857853398 -0.029393397486334 0.011999804274721
0.042289602909023 -0.024415913623447 0.028193068606016
0.027154245218747 -0.015677510786684 0.041806695431158
0.000000000000000 -0.000000000000000 -0.049815118005748
0.039186360495468 -0.000000000000000 -0.038410316117142
0.056803651667469 -0.000000000000000 -0.024791146049150
0.072097497329379 -0.000000000000000 -0.007246071120158
0.067060501396178 -0.000000000000000 0.013688667526320
0.051379603016815 -0.000000000000000 0.029664027632614
0.031789354260577 -0.000000000000000 0.042385805680769
Большое спасибо за любую помощь, которую вы можете оказать.
1 ответ
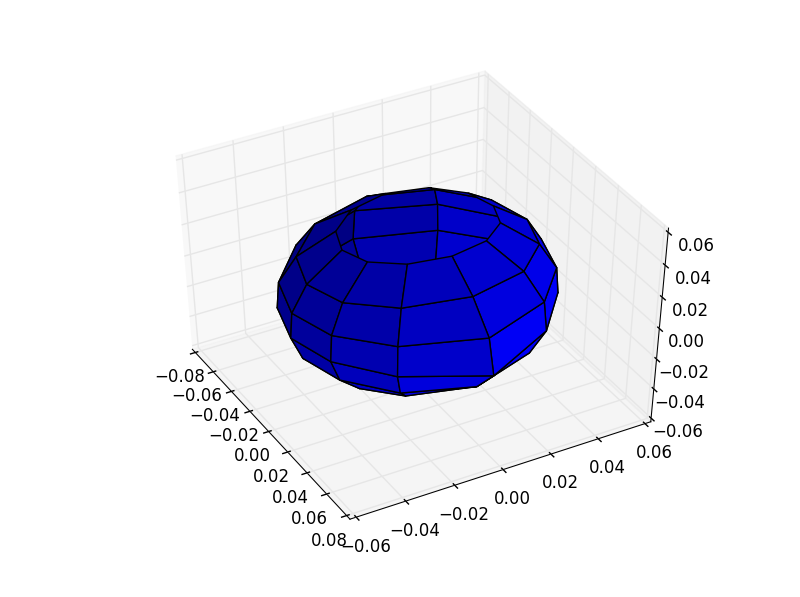
Другой ответ также применим здесь, поскольку у вас уже есть (обычный!) Меш. Однако получение уникальных значений не работает с вашими данными (по-видимому). Вместо этого я посмотрел на данные и определил вручную форму сетки, то есть в x-данных всегда есть 7 записей, прежде чем мы вернемся к x=0, Итак, следующие работы:
data = np.loadtxt('lobe1.dat')
xs = data[:,0].reshape((-1, 7))
ys = data[:,1].reshape((-1, 7))
zs = data[:,2].reshape((-1, 7))
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(xs,ys,zs, rstride=1, cstride=1,color='b')
plt.show()
Доказательство: