Когда установлены флаги переноса?

Question

Что подразумевается под "применением инструкции NEG к ненулевому операнду, всегда устанавливает флаг переноса".

Почему вычитание 2 из 1 устанавливает флаг переноса?

           00000001 (1)
 + 11111110 (-2) [в двухкомпонентной форме]
 ---------------------
CF:1       11111111 (-1) [почему здесь установлен флаг переноса???]

Answer 1

Вы могли бы просмотреть NEG a как эквивалент SUB 0, a, Если a не ноль, тогда это установит флаг переноса (поскольку это всегда приведет к переполнению без знака).

Answer 2

• Во-первых, мы знаем, когда a < b, a - b всегда может произвести перенос (одолжить).

• Во-вторых, давайте поймем, почему x86 инвертировал флаг переноса при вычитании.
  Первый пункт для человека настолько очевиден, но не для компьютера. (Предположим, использование компьютера a + (~b+1) заменить a - b сделать расчет.) Как компьютер определиться с займом? Мы можем взять 2 дополнения как часы. (По часовой стрелке означает исходное число - a против часовой стрелки означает инверсию - ~b+1)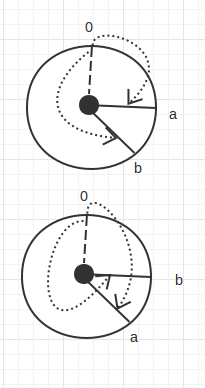
  
  Так что для компьютера, он может сказать, что (для вычитания), если a > b, a + ~b + 1 придется нести (перекрытие на картинке); если a < b, a + ~b + 1 не будет нести (разрыв на картинке).

• Заключение:
  Итак, для вычитания, если нет переноса, значит, есть заимствование; если есть перенос, значит не брать, то есть инвертировать бит переноса.

Кстати, насколько я пытался, переполнения нет (т.е. OF не установлен, когда 1 - 2.) Я не думаю, что @ Оливер прав в этом вопросе.

Answer 3

Пока неясно, пока не прочитано, как определяется флаг CF. Руководство по процессору Intel для процессоров гласит:

If the result of an arithmetic operation is treated as an unsigned integer, 
the CF flag indicates an out-of-range condition

Отрицание всего, что рассматривается как беззнаковое, очевидно, недопустимо, поскольку никакое беззнаковое значение не может перевернуться и остаться без знака (если только оно не равно нулю). Поэтому, используя метод карандаша и бумаги, вы получите совершенно противоположные результаты: "карандашный перенос = 1" при отрицании нуля и "карандашный перенос = 0" при отрицании любого другого битового шаблона.

Возможно, именно поэтому у нас есть "переносить флаг" в регистре флагов, а НЕ "переносить бит". И снова - имеется флаг переноса, указывающий, что результат операции над операндом (ами) (обработанный как беззнаковый) выходит за допустимый "диапазон без знака" для определенного количества битов.

Если значение, которое вы отрицаете, рассматривается как подписанное - вы должны посмотреть на флаг переполнения.

Ключевым моментом здесь является то, что"переносить флаг" НЕ "переносить бит". Иногда он ведет себя как один, но не всегда.

Кстати: дело не только в x86/64. Это то же самое, например, в AVR Atmel.

ARM, вероятно, сделает то же самое, так как их руководства говорят, что:

For a subtraction, including the comparison instruction CMP and the negate 
instructions NEGS and NGCS, C is set to 0 if the subtraction produced a 
borrow (that is, an unsigned underflow), and to 1 otherwise.

и вообще, документ ARM называется Carry Flag - флаг Carry/ loan, поэтому снова его не следует рассматривать как Carry BIT

Answer 4

Флаг переноса в вычитании устанавливается всякий раз, когда результат не может быть представлен в двоичном числе без знака. Число без знака всегда считается положительным.

1 - 2 дает результат, который будет -1 но -1 не может быть представлен в 8-битном формате без знака, следовательно, установлен флаг переноса.

Это происходит, даже если алгоритм вычитания имеет результат, который умещается в 8 битов, и даже если этот результат можно интерпретировать как двоичное число из 2-х дополнений с правильным результатом.

NEG Инструкция предназначена для использования с числами, которые будут интерпретироваться как числа с 2-мя дополнениями, потому что то, что делает инструкция, - это с точностью до 2-х дополнить это число, то есть изменить его знак. Знак - это свойство чисел с двумя дополнениями, а не чисел без знака.

NEG n так же, как расчет 0-nи единственный результат, который подходит для 8-битного числа без знака, это 00000000, А другой результат не будет надлежащим числом без знака.