Как преобразовать триангуляцию Делоне в формат.stl (стереолитография)?

Я нашел несколько инструментов, которые конвертируют isosurface - класс или meshgrid данные в MATLAB в формате STL. Примеры включают stlwrite и surf2stl. Чего я не могу понять, так это как взять объект delaunayTriangulation и использовать его для создания файла STL или преобразовать его в объект изоповерхности.
Основная проблема заключается в том, что я начинаю с массива граничных точек N-2 для неправильных многоугольников, поэтому у меня нет простого способа создать сетку XYZ. Если есть способ преобразовать список границ в изоповерхность внутренней области (постоянная Z-высота - все, что мне нужно), это также решит мою проблему.
В противном случае мне нужен какой-то способ конвертировать delaunayTriangulation объект во что-то, на что могут ссылаться инструменты MATLAB FEX.

отредактируйте, чтобы ответить на предложение Андер Б:

Я проверил, что мой триангулированный набор внутри MATLAB является двумерным сектором круга. Но когда я передаю данные stlwrite и импортировать в Cura Я получаю катастрофу - треугольники под прямым углом или поворачиваем пи от нужного, или того хуже. Является ли это ошибкой stlwrite Кура чувствительна к какой-то неожиданной ценности или обоим, я не могу сказать. Вот то, что начиналось как диск: 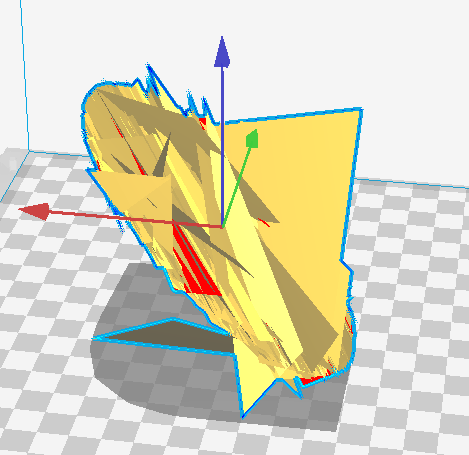Например, вот набор точек, которые определяют сектор круга. Я могу успешно создать объект delaunayTriangulation из этих данных.

>> [fcx1',fcy1']
ans =
  100.4563   26.9172
   99.9712   28.6663
   99.4557   30.4067
   98.9099   32.1378
   98.3339   33.8591
   97.7280   35.5701
   97.0924   37.2703
   96.4271   38.9591
   95.7325   40.6360
   95.0087   42.3006
   94.2560   43.9523
   93.4746   45.5906
   92.6647   47.2150
   91.8265   48.8250
   90.9604   50.4202
   90.0666   52.0000
   89.1454   53.5640
   88.1970   55.1116
   87.2217   56.6425
   86.2199   58.1561
   85.1918   59.6519
   84.1378   61.1297
   83.0581   62.5888
   81.9531   64.0288
   80.8232   65.4493
   79.6686   66.8499
   78.4898   68.2301
   77.2871   69.5896
   76.0608   70.9278
   74.8113   72.2445
   73.5391   73.5391
   72.2445   74.8113
   70.9278   76.0608
   69.5896   77.2871
   68.2301   78.4898
   66.8499   79.6686
   65.4493   80.8232
   64.0288   81.9531
   62.5888   83.0581
   61.1297   84.1378
   59.6519   85.1918
   58.1561   86.2199
   56.6425   87.2217
   55.1116   88.1970
   53.5640   89.1454
   52.0000   90.0666
   50.4202   90.9604
   48.8250   91.8265
   47.2150   92.6647
   45.5906   93.4746
   43.9523   94.2560
   42.3006   95.0087
   40.6360   95.7325
   38.9591   96.4271
   37.2703   97.0924
   35.5701   97.7280
   33.8591   98.3339
   32.1378   98.9099
   30.4067   99.4557
   28.6663   99.9712
   26.9172  100.4563
   25.1599  100.9108
   23.3949  101.3345
   21.6228  101.7274
   19.8441  102.0892
   18.0594  102.4200
   16.2692  102.7196
   14.4740  102.9879
   12.6744  103.2248
   10.8710  103.4303
    9.0642  103.6042
    7.2547  103.7467
    5.4429  103.8575
    3.6295  103.9366
    1.8151  103.9842
         0  104.0000
   -1.8151  103.9842
   -3.6295  103.9366
   -5.4429  103.8575
   -7.2547  103.7467
   -9.0642  103.6042
  -10.8710  103.4303
  -12.6744  103.2248
  -14.4740  102.9879
  -16.2692  102.7196
  -18.0594  102.4200
  -19.8441  102.0892
  -21.6228  101.7274
  -23.3949  101.3345
  -25.1599  100.9108
  -26.9172  100.4563
         0         0
Источник

2 ответа

Решение

Основываясь на ответе Андер Б., вот полная последовательность. Эти шаги обеспечивают правильную обработку даже вогнутых многоугольников.

Начнем с двух векторов, содержащих все x и y координаты. Затем:

% build the constraint list
constr=[ (1:(numel(x)-1))' (2:numel(x))' ; numel(x) 1;];
foodel = delaunayTriangulation(x',y',constr);
% get logical indices of interior triangles
inout = isInterior(foodel);

% if desired, plot the triangles  and the original points to verify.
%  triplot(foodel.ConnectivityList(inout, :),...
    foodel.Points(:,1),foodel.Points(:,2), 'r')
% hold on
%  plot(fooa.Points(:,1),fooa.Points(:,2),'g')

% now solidify
%  need to create dummy 3rd column of points for a solid
point3 = [foodel.Points,ones(numel(foodel.Points(:,1)),1)];
% pick any negative 'elevation' to make the area into a solid
[solface,solvert] = surf2solid(foodel.ConnectivityList(inout,:),...
    point3, 'Elevation', -10);  

stlwrite('myfigure.stl',solface,solvert);

Я успешно превратил некоторые "уродливые" вогнутые многоугольники в STL, которые Cura с удовольствием превращает в gCode.

Источник

STL - это просто формат для хранения информации меша в памяти, поэтому у вас есть данные, если у вас есть меш, вам просто нужно записать его в память, используя правильный формат.

Похоже, что вы вводите вершины и грани stlwrite функционировать как

stlwrite(FILE, FACES, VERTICES);

И delaunayTriangulation вывод дает вам объект, который имеет легкий доступ к этим данным, как для объекта DT, DT.Points это вершины, и DT.ConnectivityList это лица.

Вы можете прочитать больше об этом в документации, которую вы связали.

Источник
Другие вопросы по тегам