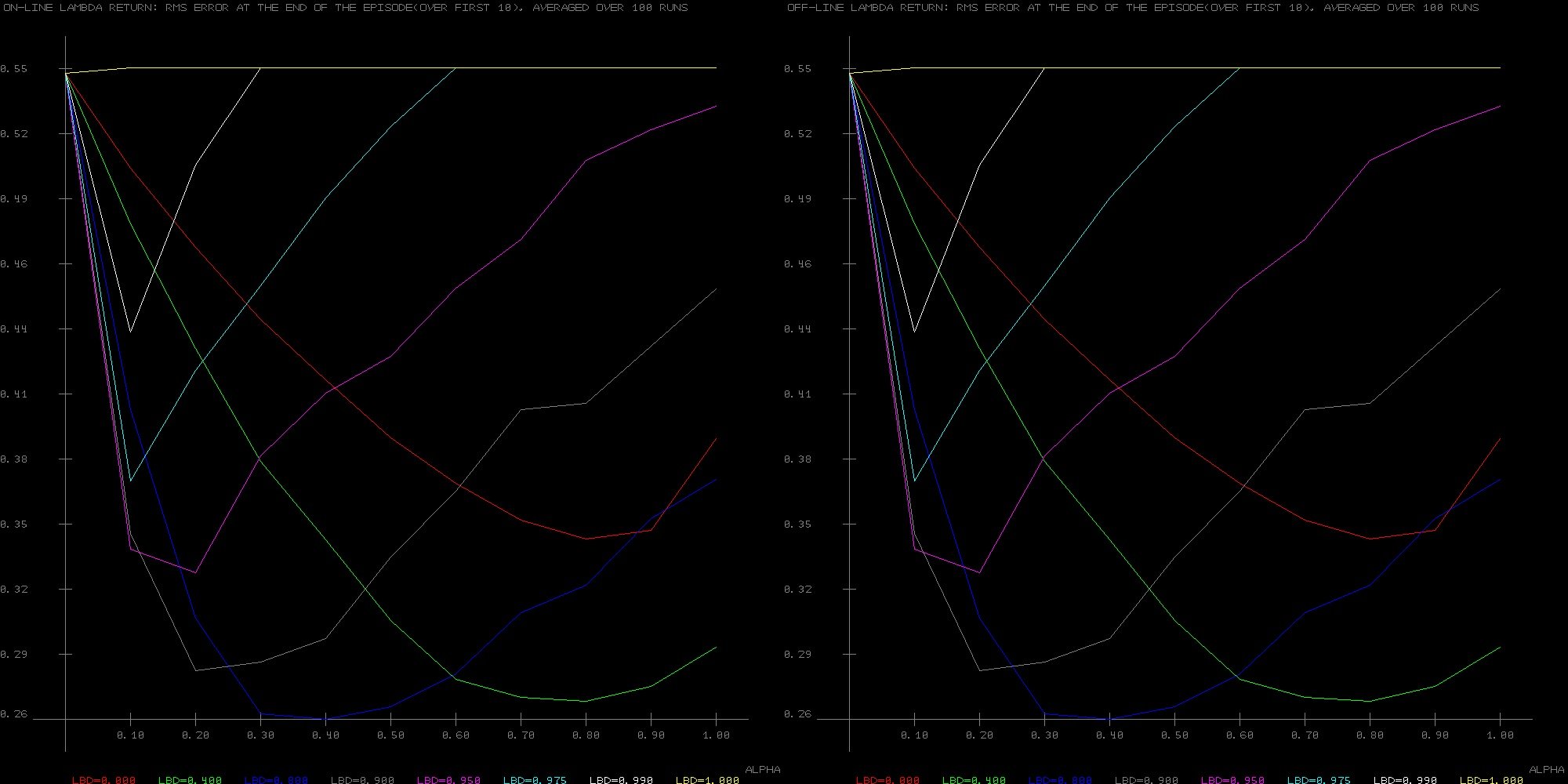
Критерии соответствия: On-line против Off-line λ-return алгоритма

Question

У меня есть некоторые проблемы с выяснением того, почему вам нужно пересматривать все временные шаги из эпизода на каждом горизонте для онлайн-версии алгоритма λ-возврата из книги:
Reinforcement Learning: An Introduction, 2nd Edition, Chapter 12, Sutton & Barto

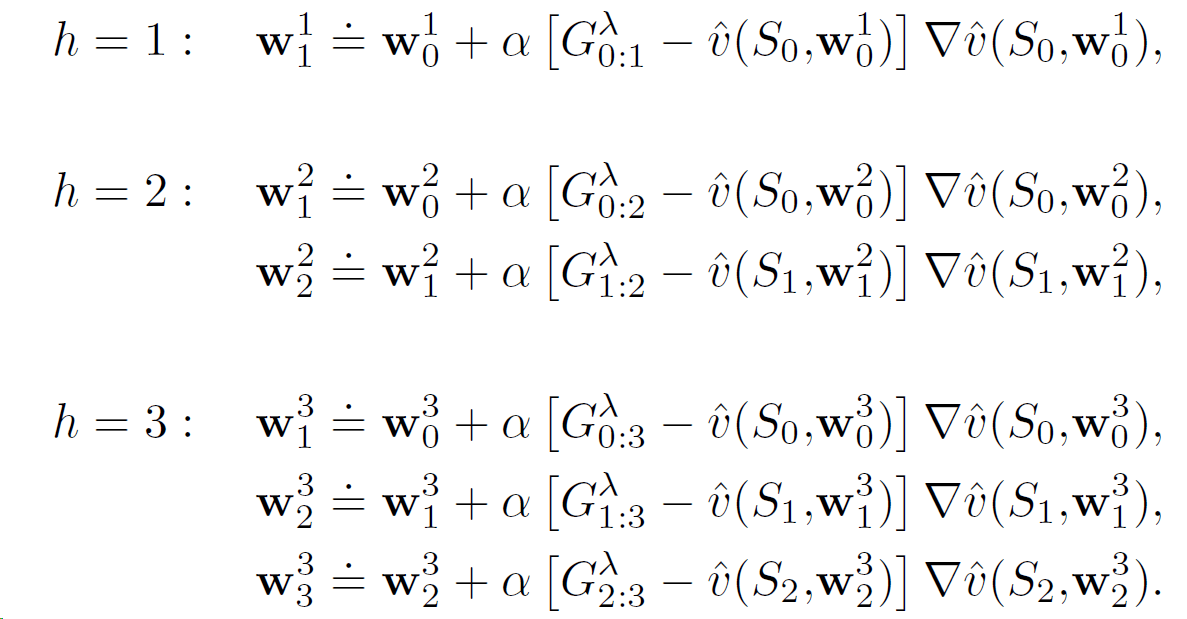
Здесь все последовательности весовых векторов W1, W2,..., Wh для каждого горизонта h начинаются с W0(веса с конца предыдущего эпизода). Однако они, похоже, не зависят от прибылей / весов предыдущего горизонта и могут быть рассчитаны независимо. Это кажется мне объясненным так только для пояснения, и вы можете рассчитать их только для конечного горизонта h=T в конце эпизода. Это будет то же самое, что сделано для автономной версии алгоритма, а фактическое правило обновления:

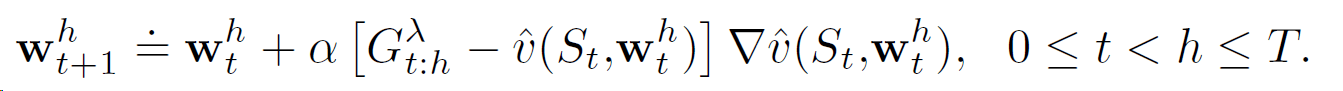
Не удивительно, что я получаю точно такие же результаты для двух алгоритмов на примере Random Walk из 19 состояний:

В книге упоминается, что онлайн-версия должна работать немного лучше, и в этом случае она должна иметь те же результаты, что и True Online TD(λ). При реализации последнего он действительно превосходит автономную версию, но я не могу понять это для простой и медленной онлайн-версии.

Любые предложения будут оценены.

Спасибо

Answer 1

Это кажется мне объясненным так только для пояснения, и вы можете рассчитать их только для конечного горизонта h=T в конце эпизода.

Это неправда. Весь смысл онлайн-алгоритма λ-возврата в том, что он онлайн: он делает обновления в течение эпизода. Это имеет решающее значение в настройке элемента управления, когда выбранные действия определяются оценками текущего значения. Даже в настройках прогнозирования, изменения веса, сделанные для более ранних горизонтов, имеют эффект.

Это связано с тем, что конечный весовой вектор из последнего горизонта всегда используется при вычислении цели обновления - усеченного лямбда-возврата. Таким образом, w_1^1 используется для вычисления всех целей для h=2, а w_2^2 используется для вычисления всех целей для h=3. Поскольку цели рассчитываются с использованием последних весовых векторов, они, как правило, более точные.

Даже в режиме прогнозирования алгоритм онлайн-возврата лямбды превосходит автономную версию, потому что цели, которые он использует, лучше.