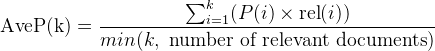MAP@k вычисление
Средняя средняя точность, вычисленная при k (для топ-k элементов в ответе), согласно вики, мл метрики в kaggle, и этот ответ: Путаница в отношении (средней) средней точности должна быть вычислена как среднее средней точности при k, где среднее Точность при k вычисляется как:
Где: P(i) - точность при отсечении i в списке; rel(i) - это индикаторная функция, равная 1, если элемент с рангом i является релевантным документом, в противном случае ноль.
Делитель min(k, number of relevant documents) имеет значение максимально возможного количества релевантных записей в ответе.
Это понимание правильно?
Всегда ли MAP@k меньше MAP, вычисляемого для всего ранжированного списка?
Меня беспокоит то, что во многих работах MAP@k вычисляется не так.
Типично, что делитель не min(k, number of relevant documents), но количество относительных документов в топ-к. Этот подход даст более высокое значение MAP@k.
HashNet: глубокое обучение хешу через продолжение " (ICCV 2017)
Код: https://github.com/thuml/HashNet/blob/master/pytorch/src/test.py
for i in range(query_num):
label = validation_labels[i, :]
label[label == 0] = -1
idx = ids[:, i]
imatch = np.sum(database_labels[idx[0:R], :] == label, axis=1) > 0
relevant_num = np.sum(imatch)
Lx = np.cumsum(imatch)
Px = Lx.astype(float) / np.arange(1, R+1, 1)
if relevant_num != 0:
APx.append(np.sum(Px * imatch) / relevant_num)
куда relevant_num это не min(k, number of relevant documents), но количество соответствующих документов в результате, которое не совпадает с общим количеством относительных документов или k.
Я неправильно читаю код?
Глубокое визуально-семантическое квантование эффективного поиска изображений CVPR 2017
Код: https://github.com/caoyue10/cvpr17-dvsq/blob/master/util.py
def get_mAPs_by_feature(self, database, query):
ips = np.dot(query.output, database.output.T)
#norms = np.sqrt(np.dot(np.reshape(np.sum(query.output ** 2, 1), [query.n_samples, 1]), np.reshape(np.sum(database.output ** 2, 1), [1, database.n_samples])))
#self.all_rel = ips / norms
self.all_rel = ips
ids = np.argsort(-self.all_rel, 1)
APx = []
query_labels = query.label
database_labels = database.label
print "#calc mAPs# calculating mAPs"
bar = ProgressBar(total=self.all_rel.shape[0])
for i in xrange(self.all_rel.shape[0]):
label = query_labels[i, :]
label[label == 0] = -1
idx = ids[i, :]
imatch = np.sum(database_labels[idx[0: self.R], :] == label, 1) > 0
rel = np.sum(imatch)
Lx = np.cumsum(imatch)
Px = Lx.astype(float) / np.arange(1, self.R+1, 1)
if rel != 0:
APx.append(np.sum(Px * imatch) / rel)
bar.move()
print "mAPs: ", np.mean(np.array(APx))
return np.mean(np.array(APx))
Где делитель rel, который вычисляется как np.sum(imatch), где imatch является двоичным вектором, который указывает, является ли запись релевантной или нет. Проблема в том, что это занимает только первое R: imatch = np.sum(database_labels[idx[0: self.R], :] == label, 1) > 0, Так np.sum(imatch) даст количество соответствующих записей в возвращенном списке размера R, но нет min(R, number of relevant entries), И обратите внимание, что значения R в работе используются меньше количества записей в БД.
Углубленное изучение двоичных хеш-кодов для быстрого поиска изображений (CVPR 2015)
Код: https://github.com/kevinlin311tw/caffe-cvprw15/blob/master/analysis/precision.m#L30-L55
buffer_yes = zeros(K,1);
buffer_total = zeros(K,1);
total_relevant = 0;
for j = 1:K
retrieval_label = trn_label(y2(j));
if (query_label==retrieval_label)
buffer_yes(j,1) = 1;
total_relevant = total_relevant + 1;
end
buffer_total(j,1) = 1;
end
% compute precision
P = cumsum(buffer_yes) ./ Ns';
if (sum(buffer_yes) == 0)
AP(i) = 0;
else
AP(i) = sum(P.*buffer_yes) / sum(buffer_yes);
end
Здесь делитель sum(buffer_yes) это число относительных документов в возвращенном списке размера k, а не min(k, number of relevant documents),
"Контролируемое изучение семантики, сохраняющей глубокое хеширование" (TPAMI 2017)
Код: https://github.com/kevinlin311tw/Caffe-DeepBinaryCode/blob/master/analysis/precision.m
Код такой же, как и в предыдущей статье.
Тот же код: https://github.com/kevinlin311tw/cvpr16-deepbit/blob/master/analysis/precision.m#L32-L55
Я что-то пропустил? Правильно ли указан код в приведенных выше документах? Почему он не совпадает с https://github.com/benhamner/Metrics/blob/master/Python/ml_metrics/average_precision.py?
Обновить
Я нашел этот закрытый вопрос, ссылаясь на ту же проблему: https://github.com/thuml/HashNet/issues/2
Правильно ли следующее утверждение?
AP является метрикой рейтинга. Если 2 верхних поиска в ранжированном списке являются релевантными (и только 2 верхними), AP составляет 100%. Вы говорите о Recall, который в этом случае действительно составляет 0,2%.
Насколько я понимаю, если мы рассматриваем AP как область под кривой PR, утверждение выше не является правильным.
PS Я сомневался, стоит ли переходить на Cross Validated или Stackru. Если вы думаете, что лучше поместить его в Cross Validated, я не возражаю. Я рассуждал, что это не теоретический вопрос, а вопрос реализации со ссылкой на реальный код.
1 ответ
Вы совершенно правы и молодцы, что нашли это. Учитывая сходство кода, я предполагаю, что есть одна исходная ошибка, а затем статьи после статей копировали плохую реализацию, не рассматривая ее внимательно.
Выпускник "akturtle" тоже совершенно прав, я собирался привести тот же пример. Я не уверен, что "кунхэ" понял аргумент, конечно, вспомнить имеет значение при вычислении средней точности.
Да, ошибка должна надувать цифры. Я просто надеюсь, что рейтинговые списки достаточно длинные и что методы достаточно разумны, так что они достигают 100% отзыва в ранжированном списке, и в этом случае ошибка не повлияет на результаты.
К сожалению, рецензентам трудно это уловить, так как обычно никто не рецензирует код статьи. Стоит связаться с авторами, чтобы попытаться заставить их обновить код, обновить свои документы с правильными номерами или, по крайней мере, не продолжать повторять ошибку. в своих будущих работах. Если вы планируете написать статью, в которой сравниваются разные методы, вы можете указать на проблему и сообщить правильные цифры (а также, возможно, те, которые содержат ошибку, просто чтобы сделать яблоки для сравнения яблок).
Чтобы ответить на ваш дополнительный вопрос:
Всегда ли MAP@k меньше MAP, вычисляемого для всего ранжированного списка?
Не обязательно, MAP@k по существу вычисляет MAP, нормализуя для потенциального случая, когда вы не можете сделать что-либо лучше, если бы только k запросов. Например, рассмотрите возвращенный ранжированный список с релевантностями: 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 и предположите, что в общей сложности 6 соответствующих документов. MAP должен быть немного выше, чем 50%, в то время как MAP@3 = 100%, потому что вы не можете сделать ничего лучше, чем извлечь 1 1 1. Но это не связано с обнаруженной вами ошибкой, так как с их ошибкой MAP@k гарантируется быть по крайней мере таким же большим, как истинная карта @k.