Рассчитать вероятности для набора биномиальных результатов, обеспеченных вероятностями для каждого события в наборе? превосходить

Question

Проблема заключается в следующем:

Допустим, в моем биномиальном дереве будут независимые события "X", и я знаю вероятность того, что все события "X" будут результатом "1" или "0". Как я могу использовать Excel для расчета вероятности каждой возможной суммы итогов? (сложение всех 1 и 0, то есть X, X-1, X-2, ..., 1, 0)

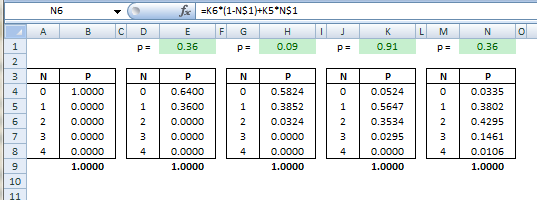
Например, у меня есть 4 события в моей серии (в конце концов я хочу до 17) с вероятностями 0,36, 0,09, 0,91, 0,36.

Как получить Excel, чтобы выплевывать:

P(score=4) = .033P(score=3) = ...P(score=2) = ...P(score=1) = ...P(score=0) = .01

Спасибо за помощь!

Answer 1

Вычисление биномиального дерева является итеративным процессом: вычисление текущего состояния из вероятностей предыдущего состояния.

Давайте заявим n имеет вероятности Pn(x) для каждого x, где x является sum total, Тогда заявите n+1 имеет вероятности:

Pn+1(x) = Pn(x) * (1-p) + Pn(x-1) * p

По состоянию n+1 вероятность иметь общую сумму x равен сумме двух вероятностей:

• вероятность иметь общую сумму x на состоянии n умноженный на вероятность иметь ноль на событии: (1-p)
• вероятность иметь общую сумму x-1 на состоянии n умноженный на вероятность иметь один на событие: p

Итак, вы начинаете с государства 0, где P0(0) = 1 и может развернуть такое дерево на любое количество событий:

Посмотрите на формулу для N6 для уточнения