Почему числа Фибоначчи значимы в информатике?
Числа Фибоначчи стали популярным введением в рекурсию для студентов, изучающих информатику, и существует сильный аргумент, что они сохраняются в природе. По этим причинам многие из нас знакомы с ними.
Они также существуют в информатике в других местах; в удивительно эффективных структурах данных и алгоритмах, основанных на последовательности.
На ум приходят два основных примера:
- Кучи Фибоначчи, которые лучше амортизируют время работы, чем биномиальные кучи.
- Поиск по Фибоначчи, который разделяет время выполнения O(log N) с двоичным поиском по упорядоченному массиву.
Есть ли какое-то специальное свойство этих чисел, которое дает им преимущество перед другими числовыми последовательностями? Это пространственное качество? Какие еще возможные приложения они могут иметь?
Мне это кажется странным, поскольку существует много последовательностей натуральных чисел, которые встречаются в других рекурсивных задачах, но я никогда не видел каталонскую кучу.
10 ответов
Числа Фибоначчи обладают множеством действительно хороших математических свойств, которые делают их превосходными в информатике. Вот несколько из них:
- Они растут в геометрической прогрессии. Одной интересной структурой данных, в которой возникает ряд Фибоначчи, является дерево AVL, форма самобалансирующегося двоичного дерева. Интуиция за этим деревом состоит в том, что каждый узел поддерживает коэффициент баланса, так что высоты левого и правого поддерева отличаются не более чем на единицу. Из-за этого вы можете думать о минимальном количестве узлов, необходимом для получения дерева AVL с высотой h, которое определяется повторением, которое выглядит как N(h + 2) ~= N(h) + N(h + 1), который очень похож на серию Фибоначчи. Если вы поработаете над математикой, вы можете показать, что число узлов, необходимое для получения дерева AVL с высотой h, равно F(h + 2) - 1. Поскольку ряд Фибоначчи растет экспоненциально быстро, это означает, что высота AVL Дерево максимально логарифмически по числу узлов, что дает вам время поиска O(lg n), которое мы знаем и любим о сбалансированных бинарных деревьях. На самом деле, если вы можете связать размер некоторой структуры с числом Фибоначчи, вы, скорее всего, получите время выполнения O(lg n) для какой-либо операции. Это реальная причина того, что кучи Фибоначчи называются кучами Фибоначчи - доказательство того, что число куч после минимума очереди включает в себя ограничение числа узлов, которые вы можете иметь на определенной глубине, числом Фибоначчи.
- Любое число может быть записано как сумма уникальных чисел Фибоначчи. Это свойство чисел Фибоначчи имеет решающее значение для работы поиска Фибоначчи вообще; Если вы не можете сложить уникальные числа Фибоначчи в любое возможное число, этот поиск не будет работать. Сравните это с множеством других серий, таких как 3n или каталонские числа. Это также отчасти то, почему многие алгоритмы, такие как степени двух, я думаю.
- Числа Фибоначчи эффективно вычислимы. Тот факт, что ряды могут быть сгенерированы чрезвычайно эффективно (вы можете получить первые n слагаемых в O(n) или любой произвольный слагаемый в O(lg n)), тогда многие алгоритмы, которые их используют, не будут практичными. Генерация каталонских чисел довольно сложна в вычислительном отношении, IIRC. Кроме того, числа Фибоначчи имеют хорошее свойство, при котором, учитывая любые два последовательных числа Фибоначчи, скажем, F(k) и F(k + 1), мы можем легко вычислить следующее или предыдущее число Фибоначчи, добавив два значения (F(k) + F(k + 1) = F(k + 2)) или вычитать их (F(k + 1) - F(k) = F(k - 1)). Это свойство используется в нескольких алгоритмах в сочетании со свойством (2) для разбиения чисел на сумму чисел Фибоначчи. Например, поиск Фибоначчи использует это для поиска значений в памяти, в то время как аналогичный алгоритм может использоваться для быстрого и эффективного вычисления логарифмов.
- Они педагогически полезны. Преподавать рекурсию сложно, и серия Фибоначчи - отличный способ ее представить. Вы можете говорить о прямой рекурсии, о запоминании или о динамическом программировании при представлении серии. Кроме того, удивительная замкнутая форма для чисел Фибоначчи часто преподается как упражнение в индукции или в анализе бесконечных рядов, а соответствующее матричное уравнение для чисел Фибоначчи обычно вводится в линейной алгебре как мотивация собственных векторов и собственных значений. Я думаю, что это одна из причин того, что они так громко во вступительных классах.
Я уверен, что есть больше причин, чем просто это, но я уверен, что некоторые из этих причин являются основными факторами. Надеюсь это поможет!
Величайший общий делитель - еще одна магия; увидеть это слишком много магии. Но числа Фибоначчи легко вычислить; также у него есть конкретное имя. Например, натуральные числа 1,2,3,4,5 имеют слишком много логики; все простые числа внутри них; сумма 1..n вычислима, каждый может производить с другими, но никто не заботится о них:)
Одна важная вещь, которую я забыл об этом - это Golden Ratio, который имеет очень важное влияние в реальной жизни (например, вам нравятся широкие мониторы:)
Последовательности Фибоначчи действительно встречаются повсюду в природе / жизни. Они полезны при моделировании роста популяций животных, роста клеток растений, формы снежинок, формы растений, криптографии и, конечно, информатики. Я слышал, что это называется паттерном ДНК природы.
Кучи Фибоначчи уже упоминались; число дочерних элементов каждого узла в куче не более log(n). Также поддерево, начинающее узел с m дочерними элементами, имеет не менее (m+2)-го числа Фибоначчи.
Торрентоподобные протоколы, которые используют систему узлов и суперузлов, используют Фибоначчи, чтобы решить, когда нужен новый суперузел и сколько подузлов он будет управлять. Они осуществляют управление узлами на основе спирали Фибоначчи (золотое сечение). Посмотрите на фото ниже, как узлы разделяются / объединяются (разбиваются от одного большого квадрата на меньшие и наоборот). Смотрите фото: http://smartpei.typepad.com/.a/6a00d83451db7969e20115704556bd970b-pi
Некоторые происшествия на природе
http://www.mcs.surrey.ac.uk/Personal/R.Knott/Fibonacci/sneezewort.GIF
http://img.blogster.com/view/anacoana/post-uploads/finger.gif
http://jwilson.coe.uga.edu/EMAT6680/Simmons/6690Pictures/pinecone3yellow.gif
Если у вас есть алгоритм, который может быть успешно объяснен в простой и лаконичной манере с понятными примерами из CS и природы, какой лучший инструмент обучения может кто-то придумать?
Просто чтобы добавить мелочи об этом, числа Фибоначчи описывают разведение кроликов. Вы начинаете с (1, 1) двух кроликов, а затем их популяция растет в геометрической прогрессии.
Для меня это про порядок и пространственные координаты.
Последовательность Фибоначчи можно использовать как часы.
Последовательность Фибоначчи позволяет вычислять золотое десятичное число за десятичной дробью.
Золотое число, умноженное само на себя, дает почти золотое число +1.
Таким образом, мы, безусловно, можем разрезать целое число на серию целых чисел, единиц, используя, например, индексы.
Я сделал первую наивную версию в коде python.(poc) для обновления.
https://gitlab.com/numbers/Numbers/-/blob/main/range.py
Таким образом, мы можем кадрировать, подсчитывать и координировать шаги вычислений и пространства памяти с этой идеально периодической системой отсчета (во времени) и, таким образом, сделать ее своего рода эквивалентом универсальной таблицы умножения. Для меня это явно отображение.
Идея состоит в том, чтобы в конечном итоге предложить троичный код с явным управлением пространствами памяти в соответствии с шагом вычислений Фибоначчи, а затем найти там все наши числа.
После этого, чтобы использовать это отображение, эту универсальную таблицу, этот фильтр: для проверки согласованности, непротиворечивости, периодичности сложных вычислимых операций, таких как эксперимент Уилера, синус, гравитация и т. д.
Звучит претенциозно, когда вы так говорите. Это не. Никто не создает золотое число или Фибоначчи. Они здесь, их дают, как плоды на дереве.
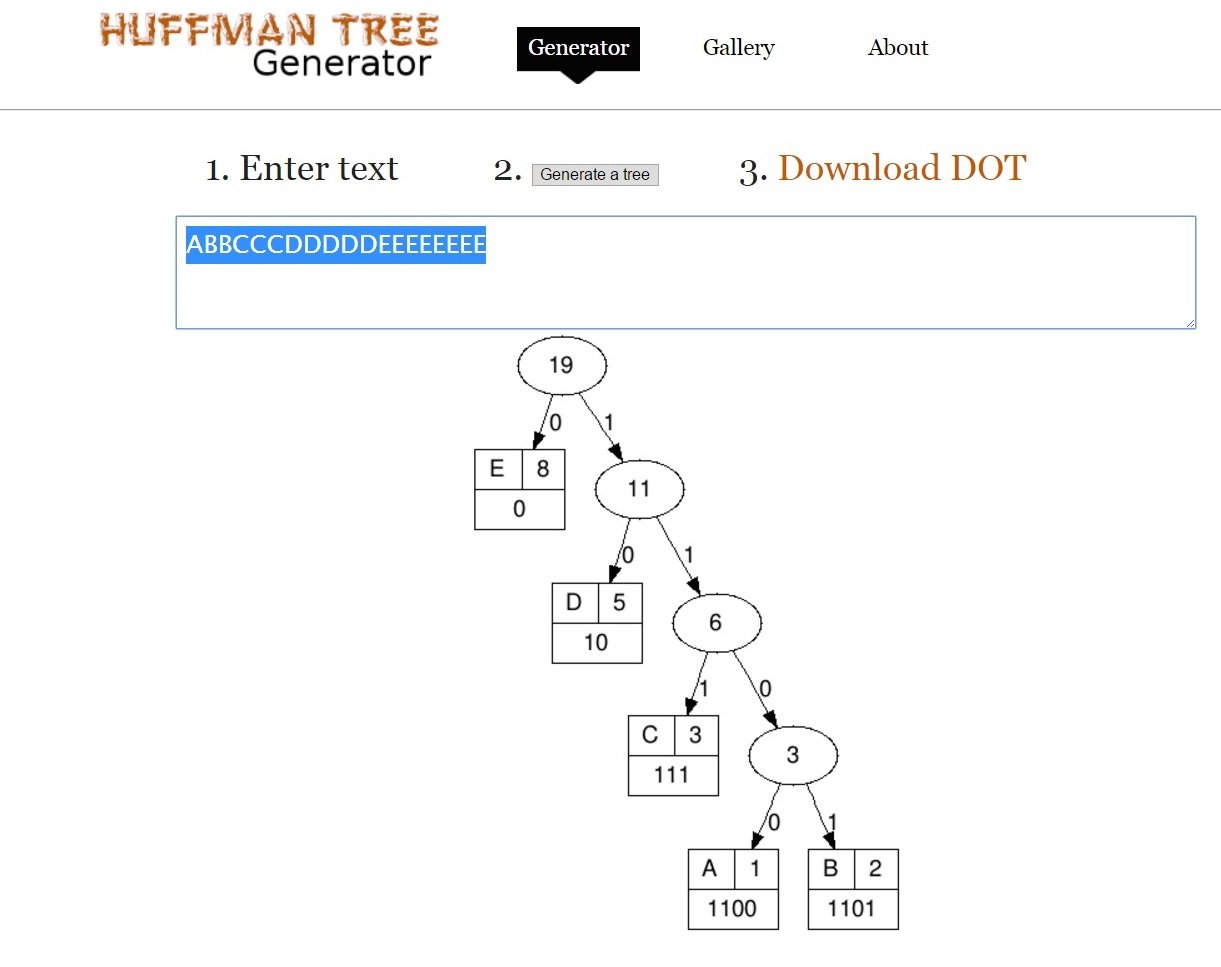
Символы с частотами, которые являются последовательными числами Фибоначчи, создают деревья Хаффмана с максимальной глубиной, которые соответствуют исходным символам, кодируемым двоичными кодами максимальной длины. Частоты символов не-Фибоначчи создают более сбалансированные деревья с более короткими кодами. Длина кода напрямую влияет на сложность описания конечного автомата, который отвечает за декодирование заданного кода Хаффмана.
Гипотеза: 1-е (fib) изображение будет сжато до 38 бит, а 2-е (равномерное) - с 50 битами. Кажется, что чем ближе ваши исходные символьные частоты к числам Фибоначчи, тем короче конечная двоичная последовательность, тем лучше сжатие, возможно, оптимальное в модели Хаффмана.
Дальнейшее чтение:
Buro, M. (1993). О максимальной длине кодов Хаффмана. Письма обработки информации, 45(5), 219-223. DOI:10.1016/0020-0190(93)90207-р
Я не думаю, что есть однозначный ответ, но одна возможность состоит в том, что операция деления множества S на два раздела S1 и S2, один из которых затем делится на подразделы S11 и S12, один из которых имеет тот же размер, что и S2 - это вероятный подход ко многим алгоритмам, который иногда можно численно описать как последовательность Фибоначчи.
Их вычисление как степень [[0,1],[1,1]] матрицы можно рассматривать как наиболее примитивную проблему исследования операций (вроде как "Дилемма заключенного" - самая примитивная проблема теории игр).
Позвольте мне добавить еще одну структуру данных к вам: деревья Фибоначчи. Они интересны, потому что вычисление следующей позиции в дереве может быть сделано простым добавлением предыдущих узлов:
http://xw2k.nist.gov/dads/html/fibonacciTree.html
Это хорошо согласуется с обсуждением templatetypedef по AVL-деревьям (дерево AVL в худшем случае может иметь структуру Фибоначчи). Я также видел буферы, расширенные по шагам Фибоначчи, а не степени двойки в некоторых случаях.