Почему мы умножаем "наиболее вероятную оценку" на 4 в трехбалльной оценке?

Question

Я использовал трехбалльную оценку для одного из моих проектов. Формула

   Three Point Estimate = (O + 4M + L ) / 6

Это означает,

  Best Estimate + 4 x Most Likely Estimate + Worst Case Estimate divided by 6

Вот

divided by 6 means, average 6

и меньше шансов на худший случай или на лучший случай. Добросовестно, наиболее вероятная оценка (M) - это то, что нужно для выполнения работы.

Но я не знаю, почему они используют 4(M), Почему они умножены на 4??? Не используйте 5,6,7 и т. Д.... почему наиболее вероятная оценка взвешенная four times столько, сколько два других значения?

Answer 1

Здесь есть вывод:

http://www.deepfriedbrainproject.com/2010/07/magical-formula-of-pert.html

В случае, если ссылка не работает, я предоставлю резюме здесь.

Итак, на шаг отступая от вопроса, цель здесь состоит в том, чтобы придумать единственную среднюю (среднюю) цифру, которую мы можем сказать, является ожидаемой цифрой для любой данной 3-балльной оценки. То есть, если бы я попытался выполнить проект X раз и сложить все затраты на попытки проекта в общей сложности $Y, то я ожидаю, что стоимость одной попытки составит $Y/X. Обратите внимание, что это число может совпадать или не совпадать с исходным режимом (наиболее вероятным) в зависимости от распределения вероятностей.

Ожидаемый результат полезен, потому что мы можем сделать такие вещи, как сложить полный список ожидаемых результатов, чтобы создать ожидаемый результат для проекта, даже если мы рассчитывали каждый отдельный ожидаемый результат по-разному.

Режим, с другой стороны, не обязательно является уникальным для каждой оценки, поэтому это одна из причин того, что он может быть менее полезным, чем ожидаемый результат. Например, каждое число от 1 до 6 является "наиболее вероятным" для броска костей, но 3,5 - это (только) ожидаемый средний результат.

Обоснование / исследование 3-балльной оценки заключается в том, что во многих (большинстве?) Реальных сценариях эти числа могут быть более точно / интуитивно оценены людьми, чем одно ожидаемое значение:

• Пессимистический исход (P)
• Оптимистичный исход (O)
• Наиболее вероятный исход (M)

Однако, чтобы преобразовать эти три числа в ожидаемое значение, нам нужно распределение вероятностей, которое интерполирует все другие (потенциально бесконечные) возможные результаты, помимо трех, которые мы произвели.

Тот факт, что мы даже делаем 3-балльную оценку, предполагает, что у нас недостаточно исторических данных, чтобы просто искать / рассчитывать ожидаемое значение для того, что мы собираемся сделать, поэтому мы, вероятно, не знаем, что на самом деле Распределение вероятностей для того, что мы оцениваем.

Идея, лежащая в основе оценок PERT, заключается в том, что, если мы не знаем фактическую кривую, мы можем подключить некоторые нормальные значения по умолчанию к бета-распределению (которое в основном представляет собой просто кривую, которую мы можем настроить для множества различных форм) и использовать эти значения по умолчанию для каждой задачи. мы можем столкнуться. Конечно, если мы знаем реальное распределение или у нас есть основания полагать, что бета-распределение по умолчанию, предписанное PERT, неверно для рассматриваемой проблемы, мы НЕ должны использовать уравнения PERT для нашего проекта.

Бета-распределение имеет два параметра A а также B которые устанавливают форму левой и правой стороны кривой соответственно. Удобно, что мы можем рассчитать режим, среднее и стандартное отклонение бета-распределения, просто зная минимальные / максимальные значения кривой, а также A а также B,

Наборы PERT A а также B к следующему для каждого проекта / оценки:

Если M > (O + P) / 2 затем A = 3 + √2 а также B = 3 - √2 в противном случае значения A а также B поменялись местами.

Теперь, случается так, что если вы сделаете это конкретное предположение о форме вашего бета-распределения, следующие формулы в точности верны:

Среднее (ожидаемое значение) = (O + 4M + P) / 6

Стандартное отклонение = (O - P) / 6

Итак, в итоге

• Формулы PERT не основаны на нормальном распределении, они основаны на бета-распределении с очень специфической формой
• Если распределение вероятностей вашего проекта соответствует распределению PERT Beta, то формула PERT в точности верна, а не является приближенной
• Маловероятно, что конкретная кривая, выбранная для PERT, соответствует любому заданному произвольному проекту, и поэтому формулы PERT будут на практике приближенными
• Если вы ничего не знаете о распределении вероятностей вашей оценки, вы также можете использовать PERT, поскольку она задокументирована, понятна многим людям и относительно проста в использовании.
• Если вы знаете что-то о распределении вероятностей вашей оценки, что говорит о том, что что-то о PERT неуместно (например, 4-кратное взвешивание по отношению к режиму), то не используйте его, вместо этого используйте то, что считаете подходящим
• Причина, по которой вы умножаете на 4, чтобы получить среднее (а не 5, 6, 7 и т. Д.), Заключается в том, что число 4 привязано к форме базовой кривой вероятности
• Конечно, PERT мог быть основан на бета-распределении, которое дает 5, 6, 7 или любое другое число при вычислении среднего значения, или даже нормальное распределение, или равномерное распределение, или почти любую другую кривую вероятности, но я ' Я полагаю, что вопрос о том, почему они выбрали кривую, которую они сделали, выходит за рамки этого ответа и, возможно, в любом случае является довольно открытым / субъективным.

Answer 2

Я копался в этом один раз. Я ловко забыл записать след, так что это из памяти.

Насколько я могу судить, документы по стандартам взяли это из учебников. Учебники получили его с оригинальных 1950-х годов, записанных в статистических журналах. Запись в журнале была основана на внутреннем отчете, подготовленном RAND как часть общей работы, проделанной для разработки PERT для программы Polaris.

И вот где тропа становится холодной. Кажется, никто не имеет четкого представления о том, почему они выбрали эту формулу. Наилучшим предположением, по-видимому, является то, что оно основано на грубом приближении нормального распределения - строго, это треугольное распределение. В основном, комковатая кривая колокольчика, предполагающая, что "вероятный случай" находится в пределах 1 стандартного отклонения от истинной средней оценки.

4 / 6ths приблизительно 66,7%, что приблизительно 68%, что приблизительно соответствует площади при нормальном распределении в пределах одного стандартного отклонения от среднего.

Все это, как говорится, есть две проблемы:

1. По сути, это сделано. Кажется, нет твердой основы для его выбора. Есть некоторая литература по Оперативным исследованиям, утверждающая альтернативные распределения В какой вселенной оценки обычно распределены вокруг истинного результата? Я бы очень хотел переехать туда.
2. Эффект повышения точности 3-точечного / PERT-метода оценки может быть больше связан с разбиением задач на подзадачи, чем с какой-либо конкретной формулой. Психологи, изучающие то, что они называют "ошибкой планирования", обнаружили, что разбивка задач - "распаковка" в их терминологии - последовательно улучшает оценки, делая их выше и, таким образом, уменьшая неточность. Так что, возможно, магия в PERT/3-point - это распаковка, а не формулы.

Answer 3

Разве это не хорошо работающий палец?

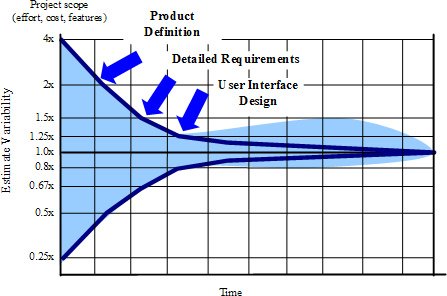
Конус неопределенности использует коэффициент 4 для начальной фазы проекта.

Книга Стива Макконнелла "Оценка программного обеспечения" основана на модели "конуса неопределенности" и дает множество "правил большого пальца". Однако каждое приблизительное число или правило большого пальца основано на статистике COCOMO или аналогичных твердых исследованиях, моделях или исследованиях.

Answer 4

В идеале эти факторы для O, M и L выводятся с использованием исторических данных для других проектов в той же компании в той же среде. Другими словами, у компании должно быть 4 проекта, выполненных в рамках оценки M, 1 в рамках O и 1 в рамках L. Если моя компания / команда завершила 1 проект в рамках первоначальной оценки O, 2 проекта в рамках M и 2 в рамках L, я бы использовал другая формула - (O + 2M + 2L) / 5. Имеет ли смысл?

Answer 5

На конус неопределенности было упомянуто выше... это хорошо известный фундаментальный элемент, используемый в методах гибкой оценки.

Но в чем проблема? Разве это не выглядит слишком симметрично - как будто это не естественно, не основано на реальных данных?

Если ты когда-либо думал об этом, то ты прав. Конус неопределенности, показанный на рисунке выше, составлен на основе вероятностей... не фактических необработанных данных из реальных проектов (но в большинстве случаев он используется как таковой).

Лоран Боссавит написал книгу, а также выступил с докладом, в котором он представил свои исследования о том, как появился этот конус (и другие "факты", которые мы часто верим в разработку программного обеспечения):

Лепреконы разработки программного обеспечения

https://www.amazon.com/Leprechauns-Software-Engineering-Laurent-Bossavit/dp/2954745509/

https://www.youtube.com/watch?v=0AkoddPeuxw

Есть ли реальные данные, подтверждающие конус неопределенности? Самым близким, который он смог найти, был конус, который может увеличиваться в 10 раз в положительном направлении Y (так что мы можем быть в 10 раз меньше по нашей оценке с точки зрения проекта, который в итоге будет в 10 раз длиннее).

Вряд ли кто-нибудь оценит проект, который закончится в 4 раза раньше... или... задохнется... в 10 раз раньше.