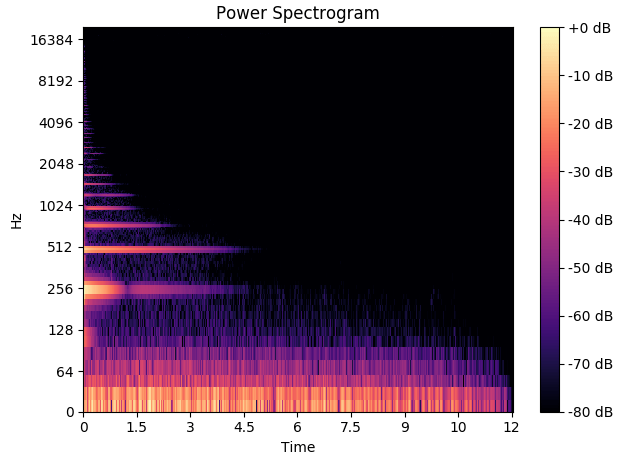
Гармонический спектр продуктов для одной гитарной ноты Python
Я пытаюсь определить высоту ноты B3, сыгранной на гитаре. Аудио можно найти здесь.
Как вы можете видеть, видно, что основной шаг составляет около 250 Гц, что соответствует ноте B3.
Он также содержит большое количество гармоник, и именно поэтому я решил использовать HPS здесь. Я использую этот код для определения высоты тона:
def freq_from_hps(signal, fs):
"""Estimate frequency using harmonic product spectrum
Low frequency noise piles up and overwhelms the desired peaks
"""
N = len(signal)
signal -= mean(signal) # Remove DC offset
# Compute Fourier transform of windowed signal
windowed = signal * kaiser(N, 100)
# Get spectrum
X = log(abs(rfft(windowed)))
# Downsample sum logs of spectra instead of multiplying
hps = copy(X)
for h in arange(2, 9): # TODO: choose a smarter upper limit
dec = decimate(X, h)
hps[:len(dec)] += dec
# Find the peak and interpolate to get a more accurate peak
i_peak = argmax(hps[:len(dec)])
i_interp = parabolic(hps, i_peak)[0]
# Convert to equivalent frequency
return fs * i_interp / N # Hz
Моя частота дискретизации 40000. Однако вместо получения результата, близкого к 250 Гц (примечание B3), я получаю 0,66 Гц. Как это возможно?
Я также пытался с помощью метода автокорреляции из того же репо, но я также получаю плохие результаты, такие как 10000 Гц.
Благодаря полученному ответу я понял, что должен применить фильтр для удаления низких частот в сигнале. Как я могу это сделать? Есть ли несколько способов сделать это, и какой из них рекомендуется?
ОБНОВЛЕНИЕ СТАТУСА:
Предложенный ответом фильтр верхних частот работает. Если я применяю функцию в ответе к своему аудиосигналу, он правильно отображает около 245 Гц. Однако я бы хотел отфильтровать весь сигнал, а не только его часть. Нота может находиться в середине сигнала или сигнал может содержать более одной ноты (я знаю, что решение - это обнаружение начала, но мне любопытно узнать, почему это не работает). Вот почему я отредактировал код для возврата filtered_audio,
Проблема в том, что если я это сделаю, хотя шум был правильно удален (см. Скриншот). Я получаю 0,05 в результате.
1 ответ
Исходя из расстояний между гармониками в спектрограмме, я бы оценил шаг примерно в 150-200 Гц. Итак, почему алгоритм обнаружения высоты звука не обнаруживает высоту, которую мы видим на спектрограмме? У меня есть несколько догадок:
Примечание длится всего несколько секунд. В начале есть красивый набор гармоник с 10 или более гармониками! Они быстро исчезают и даже не видны через 5 секунд. Если вы пытаетесь оценить высоту звука всего сигнала, ваша оценка может быть загрязнена "высотой звука" в течение 5–12 секунд. Попробуйте вычислить высоту тона только в течение первых 1-2 секунд.
Слишком много низкочастотного шума. На спектрограмме вы можете видеть большую мощность в диапазоне от 0 до 64 Гц. Это не часть гармоник, поэтому вы можете попробовать удалить их с помощью фильтра верхних частот.
Вот код, который делает эту работу:
import numpy as np
from scipy.io import wavfile
from scipy import signal
import matplotlib.pyplot as plt
from frequency_estimator import freq_from_hps
# downloaded from https://github.com/endolith/waveform-analyzer/
filename = 'Vocaroo_s1KZzNZLtg3c.wav'
# downloaded from http://vocaroo.com/i/s1KZzNZLtg3c
# Parameters
time_start = 0 # seconds
time_end = 1 # seconds
filter_stop_freq = 70 # Hz
filter_pass_freq = 100 # Hz
filter_order = 1001
# Load data
fs, audio = wavfile.read(filename)
audio = audio.astype(float)
# High-pass filter
nyquist_rate = fs / 2.
desired = (0, 0, 1, 1)
bands = (0, filter_stop_freq, filter_pass_freq, nyquist_rate)
filter_coefs = signal.firls(filter_order, bands, desired, nyq=nyquist_rate)
# Examine our high pass filter
w, h = signal.freqz(filter_coefs)
f = w / 2 / np.pi * fs # convert radians/sample to cycles/second
plt.plot(f, 20 * np.log10(abs(h)), 'b')
plt.ylabel('Amplitude [dB]', color='b')
plt.xlabel('Frequency [Hz]')
plt.xlim((0, 300))
# Apply high-pass filter
filtered_audio = signal.filtfilt(filter_coefs, [1], audio)
# Only analyze the audio between time_start and time_end
time_seconds = np.arange(filtered_audio.size, dtype=float) / fs
audio_to_analyze = filtered_audio[(time_seconds >= time_start) &
(time_seconds <= time_end)]
fundamental_frequency = freq_from_hps(audio_to_analyze, fs)
print 'Fundamental frequency is {} Hz'.format(fundamental_frequency)