Идеальный алгоритм для нахождения всех путей в графе

Question

Давайте возьмем этот график для примера:

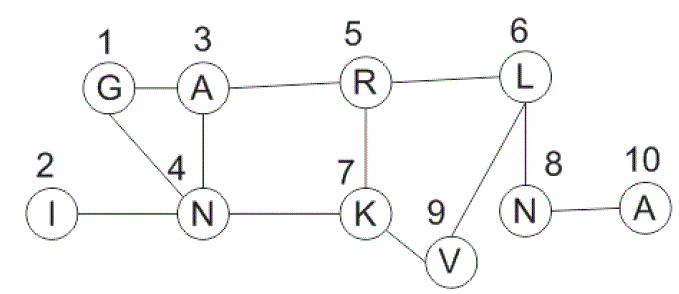
Теперь предположим, что я начинаю с вершины 3 и хочу найти вершину 7. При первом поиске по глубине (в зависимости от реализации) сначала будут рассматриваться дочерние элементы. Теперь в нашем примере ради аргумента я начинаю с вершины 2, затем перехожу к вершине 4 и вершине 2, возвращаюсь к вершине и перехожу к вершине 7, проблема решена.

Что бы я хотел: я хотел бы получить все возможные пути, которые позволили бы мне перейти от x к y (например, от 3 до 7: 3,1,4,7 - 3,5,7 - 3,4,7 - 3,5,6,9,7). Это я не получаю из глубины первого поиска.

Какой алгоритм вы бы предложили?

Спасибо!

Answer 1

Вы должны использовать модифицированный алгоритм BFS ( http://en.wikipedia.org/wiki/Breadth-first_search). В каждой вершине вы должны сохранить список соседей, которые ведут к этой вершине (предшественники), вместо того, чтобы иметь только 1 соседа, ведущего к этой вершине.

Если вы хотите найти все пути из этого, вам просто нужно начать с конечного узла и разветвлять свой путь в каждой вершине, которая имеет более 1 предшественника, и идти по пути, созданному предшественниками в каждой вершине, пока вы не доберетесь, чтобы начать узел с все ветки у вас есть.

РЕДАКТИРОВАТЬ: Вы можете использовать алгоритм DSF вместо BFS и изменить его таким же образом.