Нахождение центра листовки полигона?

У меня есть набор полигонов листовок на карте, которую я создал. Каждый многоугольник представляет что-то свое. Конкретный набор информации отображается во всплывающем окне в зависимости от страницы, на которой находится пользователь. Мне нужно найти способ сделать "всплывающий" пузырь открытым в центре многоугольника, который он представляет.

Каждый многоугольник нарисован с использованием следующего кода:

var L20 = [
    [74.0995, -99.92615],
    [74.14008, -99.4043],
    [74.07691, -99.33838],
    [74.03617, -99.86023]
];



var L19 = [
    [74.02559, -99.84924],
    [74.06636, -99.32739],
    [74.0029, -99.26147],
    [73.96197, -99.77783]
];

var L18 = [
    [73.95142, -99.76684],
    [73.99235, -99.25048],
    [73.92889, -99.18456],
    [73.8878, -99.69543]
];

var set1 = L.polygon([L20, L19, L18], {
    color: "#fff",
    weight: 1,
    stroke: true,
    opacity: 0.05,
    fillColor: "#346B1F",

}).addTo(map);

Всплывающее окно рисуется с использованием следующего кода:

var popup = L.popup({})
    .setLatLng([73.64017, -100.32715])
    .setContent(content).openOn(map);
    var popup = L.popup();

Поэтому мне нужно найти способ .setLatLang определить или получить центр многоугольника.

Я придумал 3 решения, которые могут работать, не знаю, как это сделать.

  1. найдите способ использовать координаты многоугольника, чтобы определить центр многоугольника, в котором откроется всплывающее окно.

  2. вызовите одну точку многоугольника, затем сместите позицию всплывающего окна.

  3. Используйте идентификатор для каждого многоугольника, чтобы каждое всплывающее окно знало область окна (многоугольник), в которой оно может быть открыто.

Может кто-то помочь мне, пожалуйста?

Источник

5 ответов

Решение

Есть несколько способов приблизить центр тяжести многоугольника.

Самый простой (но наименее точный метод) - получить центр ограничительной рамки, содержащей многоугольник, как предложил Ярл, используя polygon.getBounds().getCenter();

Первоначально я ответил на вопрос формулой для нахождения центра тяжести точек, которую можно найти путем усреднения координат ее вершин.

var getCentroid = function (arr) { 
    return arr.reduce(function (x,y) {
        return [x[0] + y[0]/arr.length, x[1] + y[1]/arr.length] 
    }, [0,0]) 
}

centerL20 = getCentroid(L20);

Хотя центр тяжести точек является достаточно близким приближением, чтобы обмануть меня, комментатор отметил, что это не центр тяжести многоугольника.

Реализация, основанная на формуле для центроида несамопересекающегося замкнутого многоугольника, дает правильный результат:

var getCentroid2 = function (arr) {
    var twoTimesSignedArea = 0;
    var cxTimes6SignedArea = 0;
    var cyTimes6SignedArea = 0;

    var length = arr.length

    var x = function (i) { return arr[i % length][0] };
    var y = function (i) { return arr[i % length][1] };

    for ( var i = 0; i < arr.length; i++) {
        var twoSA = x(i)*y(i+1) - x(i+1)*y(i);
        twoTimesSignedArea += twoSA;
        cxTimes6SignedArea += (x(i) + x(i+1)) * twoSA;
        cyTimes6SignedArea += (y(i) + y(i+1)) * twoSA;
    }
    var sixSignedArea = 3 * twoTimesSignedArea;
    return [ cxTimes6SignedArea / sixSignedArea, cyTimes6SignedArea / sixSignedArea];        
}
Источник

С некоторого времени Leaflet имеет встроенный метод getCenter():

polygon.getBounds().getCenter();
Источник

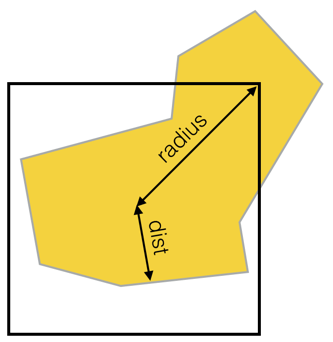
Проблема, которую вы пытаетесь решить, называется проблемой полюса недоступности. Поиск лучшего места для размещения метки в многоугольнике не полностью решается путем нахождения центра ограничительной рамки. Рассмотрим многоугольник в форме буквы U. Центр ограничивающего прямоугольника помещает метку вне многоугольника. Мне понадобилась целая вечность, чтобы найти эту выдающуюся библиотеку: https://github.com/mapbox/polylabel

Из README.MD:

Быстрый алгоритм обнаружения полюса недоступности полигона, наиболее удаленной внутренней точки от контура многоугольника (не путать с центроидом), реализован в виде библиотеки JavaScript. Полезно для оптимального размещения текстовой метки на многоугольнике.

Это алгоритм итеративной сетки, вдохновленный работой Garcia-Castellanos & Lombardo, 2007. В отличие от приведенного в статье, этот алгоритм:

  • гарантирует поиск глобального оптимума в пределах заданной точности
  • во много раз быстрее (в 10-40 раз)

Использование:

Учитывая координаты многоугольника в GeoJSON-подобном формате и точности (по умолчанию 1.0), Polylabel возвращает координату полюса недоступности в формате [x, y].

var p = polylabel(polygon, 1.0);

Полюс Недоступности

Как работает алгоритм:

Это итеративный алгоритм, основанный на сетке, который начинается с накрытия многоугольника большими квадратными ячейками, а затем итеративно разделяет их по порядку наиболее многообещающих, в то же время агрессивно отбрасывая неинтересные ячейки.

  1. Создайте начальные квадратные ячейки, которые полностью покрывают многоугольник (с размером ячейки, равным либо ширине, либо высоте, в зависимости от того, что меньше). Вычислите расстояние от центра каждой ячейки до внешнего многоугольника, используя отрицательное значение, если точка находится за пределами многоугольника (определяется методом приведения лучей).
  2. Поместите ячейки в приоритетную очередь, отсортированную по максимальному потенциальному расстоянию от точки внутри ячейки, определенной как сумма расстояния от центра и радиуса ячейки (равная cell_size * sqrt(2) / 2).
  3. Вычислите расстояние от центра тяжести многоугольника и выберите его как первое "лучшее на данный момент".
  4. Вытащите ячейки из очереди приоритетов одну за другой. Если расстояние ячейки лучше, чем текущее, сохраните его как таковой. Затем, если ячейка потенциально содержит лучшее решение, чем текущее наилучшее (cell_max - best_dist > precision), разделите его на 4 дочерние ячейки и поместите их в очередь.
  5. Остановите алгоритм, когда мы исчерпаем очередь, и вернем лучший центр ячейки в качестве полюса недоступности. Он будет гарантированно быть глобальным оптимумом при заданной точности.

Самая дальняя внутренняя точка от контура многоугольника

Источник

При условии, что у каждого многоугольника есть только 4 стороны, это просто

var L20 = [
[74.0995, -99.92615],
[74.14008, -99.4043],
[74.07691, -99.33838],
[74.03617, -99.86023]
];

используя этот пример, получим max и min lat: 74.03617 и 74.14008 соответственно, то же самое для long: -99.92615 и 99.33838 соответственно

Затем получите среднее значение для каждого: (max - min) / 2 = 0,051955 и -0,293885, затем добавьте их к минимальному количеству

дает вам центр 74.088125, -99.632265

Источник

Чтобы переместить многоугольник в поле зрения и отцентрировать его, используйте:

          map.fitBounds(poly.getBounds())

Это также позволит правильно установить уровень масштабирования.

Источник
Другие вопросы по тегам