Интеграция хаотических систем

Question

У меня есть 3 уравнения следующим образом

u'= -a*(u-v)

v'= c*u-v-u*w

w'= -b*w+u*v
a=5.0 b=0.9 and c=8.2

Я пытаюсь использовать scipy.integrate.odeint решить от t = 0 до t=10 Мои начальные условия: u(0)=0, v(0)=1.0 и w(0)=2.0 Я не могу много полезных замечаний по scipy.integrate.odeint. Поэтому мог бы воспользоваться некоторыми советами по использованию этого модуля для моей проблемы.

Answer 1

scipy.integrate.odeint принимает функцию для интеграции начальных значений для зависимых переменных (ваш u, v, w) и сетка значений времени. Любые дополнительные аргументы, которые нужны вашей функции (например, a, b а также c) передаются как args,

Определяемая вами функция должна принимать вектор значений, скажем, X, (который вы можете распаковать в u, v а также w), момент времени, которому они соответствуют, и любые дополнительные аргументы и должны возвращать первые производные X по отношению к времени в этот момент времени.

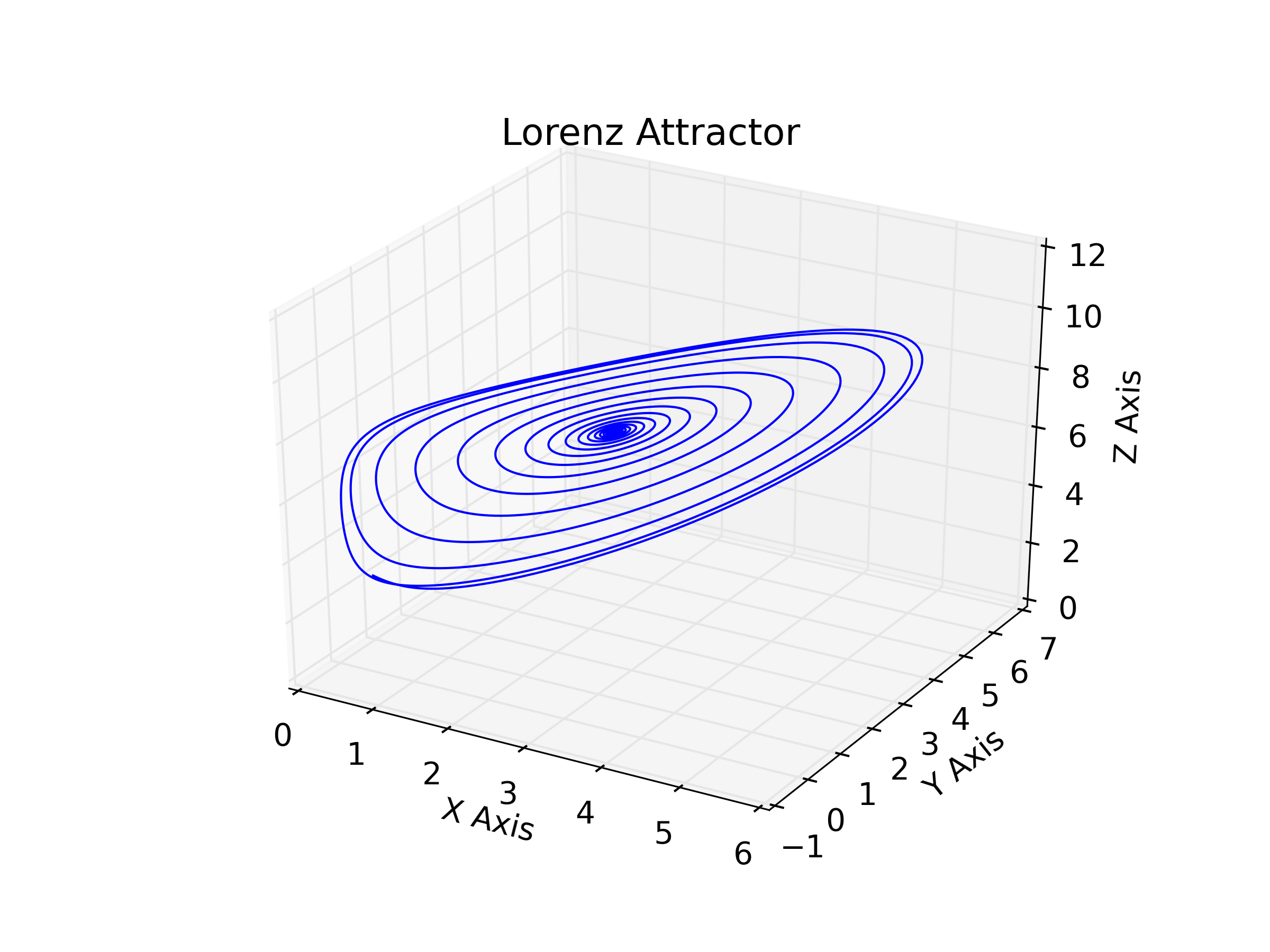
Визуализация аттрактора Лоренца является предметом одного из примеров галереи Matplotlib.

import numpy as np
from scipy.integrate import odeint

a, b, c = 5, 0.9, 8.2
u0, v0, w0 = 0, 1, 2

def lorenz(X, t, a, b, c):
    u, v, w = X
    up = -a*(u - v)
    vp = c*u - v - u*w
    wp = -b*w + u*v
    return up, vp, wp

t = np.linspace(0, 100, 10000)
f = odeint(lorenz, (u0, v0, w0), t, args=(a, b, c))
x, y, z = f.T

import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

fig = plt.figure()
ax = fig.gca(projection='3d')

ax.plot(x, y, z)
ax.set_xlabel("X Axis")
ax.set_ylabel("Y Axis")
ax.set_zlabel("Z Axis")
ax.set_title("Lorenz Attractor")

plt.show()