Правильно ли использовать метод JavaScript Array.sort() для перемешивания?
Я помогал кому-то с его JavaScript-кодом, и мои глаза привлекли внимание к следующему разделу:
function randOrd(){
return (Math.round(Math.random())-0.5);
}
coords.sort(randOrd);
alert(coords);
Мое первое, хотя было: эй, это не может работать! Но затем я немного поэкспериментировал и обнаружил, что, по крайней мере, он действительно дает хорошо рандомизированные результаты.
Затем я выполнил некоторый поиск в Интернете и почти наверху нашел статью, из которой этот код был скопирован наиболее естественным образом. Выглядел как довольно респектабельный сайт и автор...
Но мое внутреннее чувство говорит мне, что это должно быть неправильно. Тем более что алгоритм сортировки не указан стандартом ECMA. Я думаю, что разные алгоритмы сортировки приведут к различным неравномерным перемешиваниям. Некоторые алгоритмы сортировки могут даже бесконечно зацикливаться...
Но что вы думаете?
И как еще один вопрос... как бы я теперь оценил, насколько случайны результаты этой техники тасования?
Обновление: я сделал некоторые измерения и опубликовал результаты ниже как один из ответов.
13 ответов
Это никогда не был мой любимый способ перетасовки, отчасти потому, что, как вы говорите, это зависит от реализации. В частности, мне кажется, что я помню, что стандартная библиотека, сортирующая из Java или.NET (не знаю, какая именно), часто может обнаружить, если вы столкнулись с противоречивым сравнением между некоторыми элементами (например, вы сначала заявляете A < B а также B < C, но потом C < A).
Это также приводит к более сложному (с точки зрения времени выполнения) перемешиванию, чем вам действительно нужно.
Я предпочитаю алгоритм перемешивания, который эффективно разбивает коллекцию на "перемешанные" (в начале коллекции, изначально пустые) и "не перемешанные" (остальная часть коллекции). На каждом шаге алгоритма выберите случайный элемент без тасовки (который может быть первым) и поменяйте его местами с первым элементом без тасования - затем обработайте его как тасованный (то есть мысленно переместите раздел, чтобы включить его).
Это O(n) и требует только n-1 вызовов генератора случайных чисел, что приятно. Он также производит настоящую случайную последовательность - любой элемент имеет шанс 1/n оказаться в каждом пространстве, независимо от его исходного положения (при условии разумного значения ГСЧ). Сортированная версия приближается к равномерному распределению (при условии, что генератор случайных чисел не выбирает одно и то же значение дважды, что весьма маловероятно, если он возвращает случайные двойные числа), но мне проще рассуждать о случайной версии:)
Этот подход называется перетасовкой Фишера-Йейтса.
Я бы посчитал наилучшей практикой один раз кодировать этот случайный порядок и использовать его везде, где вам нужно перемешивать элементы. Тогда вам не нужно беспокоиться о реализации сортировки с точки зрения надежности или сложности. Это всего лишь несколько строк кода (которые я не буду пытаться в JavaScript!)
В статье Википедии о тасовании (и, в частности, разделе алгоритмов тасования) говорится о сортировке случайной проекции - стоит прочитать раздел о плохих реализациях тасования в целом, так что вы знаете, чего следует избегать.
После того, как Джон уже рассмотрел теорию, вот реализация:
function shuffle(array) {
var tmp, current, top = array.length;
if(top) while(--top) {
current = Math.floor(Math.random() * (top + 1));
tmp = array[current];
array[current] = array[top];
array[top] = tmp;
}
return array;
}
Алгоритм O(n)тогда как сортировка должна быть O(n log n), В зависимости от накладных расходов на выполнение кода JS по сравнению с нативным sort() функция, это может привести к заметной разнице в производительности, которая должна увеличиваться с размерами массива.
В комментариях к ответу Бобобо я заявил, что рассматриваемый алгоритм может не давать равномерно распределенные вероятности (в зависимости от реализации sort()).
Мой аргумент выглядит следующим образом: алгоритм сортировки требует определенного числа c сравнений, например c = n(n-1)/2 для Bubblesort. Наша функция случайного сравнения делает результат каждого сравнения одинаково вероятным, т.е. 2^c одинаково вероятные результаты. Теперь каждый результат должен соответствовать одному из n! перестановки элементов массива, что делает невозможным равномерное распределение в общем случае. (Это упрощение, так как фактическое число необходимых сравнений зависит от входного массива, но утверждение все еще должно сохраняться.)
Как отметил Джон, это само по себе не является основанием для предпочтения Фишера-Йейтса использованию sort(), поскольку генератор случайных чисел также отобразит конечное число псевдослучайных значений в n! Перестановки. Но результаты Фишера-Йейтса должны быть еще лучше:
Math.random() производит псевдослучайное число в диапазоне [0;1[, Поскольку JS использует значения с плавающей запятой двойной точности, это соответствует 2^x возможные значения где 52 ≤ x ≤ 63 (Мне лень найти фактическое число). Распределение вероятностей, созданное с использованием Math.random() перестанет вести себя хорошо, если число атомных событий будет того же порядка.
При использовании Фишера-Йейтса соответствующим параметром является размер массива, который никогда не должен приближаться 2^52 из-за практических ограничений.
При сортировке с использованием функции случайного сравнения функция в основном заботится только о том, является ли возвращаемое значение положительным или отрицательным, поэтому это никогда не будет проблемой. Но есть похожий: поскольку функция сравнения хорошо себя ведет, 2^c возможные результаты, как указано, одинаково вероятны. Если c ~ n log n затем 2^c ~ n^(a·n) где a = constчто делает по крайней мере возможным 2^c такой же величины, как (или даже меньше) n! и, таким образом, приводит к неравномерному распределению, даже если алгоритм сортировки, где отображать на перестановки равномерно. Если это имеет какое-либо практическое влияние, вне меня.
Реальная проблема заключается в том, что алгоритмы сортировки не гарантируют равномерное отображение на перестановки. Легко видеть, что Mergesort работает как симметрично, но рассуждения о чем-то вроде Bubblesort или, что более важно, о Quicksort или Heapsort, нет.
Итог: пока sort() использует Mergesort, вы должны быть в достаточной безопасности, за исключением крайних случаев (по крайней мере, я надеюсь, что 2^c ≤ n! это угловой случай), если нет, все ставки выключены.
Я сделал несколько измерений того, насколько случайны результаты этого случайного рода...
Моя техника заключалась в том, чтобы взять небольшой массив [1,2,3,4] и создать все (4! = 24) его перестановки. Затем я применил бы функцию перемешивания к массиву большое количество раз и посчитал, сколько раз генерируется каждая перестановка. Хороший алгоритм перетасовки распределяет результаты довольно равномерно по всем перестановкам, в то время как плохой не даст такой равномерный результат.
Используя приведенный ниже код, я протестировал Firefox, Opera, Chrome, IE6/7/8.
Удивительно для меня, но случайная сортировка и реальное перемешивание создали одинаково равномерное распределение. Похоже, что (как многие и предполагали) основные браузеры используют сортировку слиянием. Это, конечно, не означает, что не может быть браузера, который работает по-другому, но я бы сказал, что это означает, что этот метод случайной сортировки достаточно надежен для использования на практике.
РЕДАКТИРОВАТЬ: этот тест не действительно правильно измерить случайность или отсутствие таковой. Смотрите другой ответ, который я написал.
Но с точки зрения производительности функция случайного воспроизведения, предложенная Кристофом, была явным победителем. Даже для небольших четырехэлементных массивов реальное перемешивание выполнялось примерно в два раза быстрее, чем случайная сортировка!
// Функция перемешивания, опубликованная Cristoph.
var shuffle = function(array) {
var tmp, current, top = array.length;
if(top) while(-top) {
current = Math.floor(Math.random() * (top + 1));
tmp = array[current];
array[current] = array[top];
массив [top] = tmp;
}
возвращаемый массив;
};
// функция случайной сортировки
var rnd = function() {
вернуть Math.round(Math.random())-0,5;
};
var randSort = function(A) {
вернуть A.sort(rnd);
};
перестановки var = function(A) {
if (A.length == 1) {
возврат [A];
}
еще {
var perms = [];
для (var i=0; i
Интересно, что Microsoft использовала ту же технику на своей странице случайного выбора браузера.
Они использовали немного другую функцию сравнения:
function RandomSort(a,b) {
return (0.5 - Math.random());
}
Выглядит почти так же, но оказалось, что это не так случайно...
Поэтому я снова сделал несколько тестов с той же методологией, которая использовалась в связанной статье, и действительно - оказалось, что метод случайной сортировки дал неверные результаты. Новый тестовый код здесь:
function shuffle(arr) {
arr.sort(function(a,b) {
return (0.5 - Math.random());
});
}
function shuffle2(arr) {
arr.sort(function(a,b) {
return (Math.round(Math.random())-0.5);
});
}
function shuffle3(array) {
var tmp, current, top = array.length;
if(top) while(--top) {
current = Math.floor(Math.random() * (top + 1));
tmp = array[current];
array[current] = array[top];
array[top] = tmp;
}
return array;
}
var counts = [
[0,0,0,0,0],
[0,0,0,0,0],
[0,0,0,0,0],
[0,0,0,0,0],
[0,0,0,0,0]
];
var arr;
for (var i=0; i<100000; i++) {
arr = [0,1,2,3,4];
shuffle3(arr);
arr.forEach(function(x, i){ counts[x][i]++;});
}
alert(counts.map(function(a){return a.join(", ");}).join("\n"));
Я разместил на своем веб-сайте простую тестовую страницу, показывающую смещение вашего текущего браузера по сравнению с другими популярными браузерами, использующими различные методы перемешивания. Это показывает ужасный уклон просто использования Math.random()-0.5еще один случайный случайный случай, и метод Фишера-Йейтса, упомянутый выше.
Вы можете видеть, что в некоторых браузерах 50% -ная вероятность того, что определенные элементы не изменятся, вообще не изменится во время "перемешивания"!
Примечание: вы можете сделать реализацию Fisher-Yates shuffle с помощью @Christoph немного быстрее для Safari, изменив код на:
function shuffle(array) {
for (var tmp, cur, top=array.length; top--;){
cur = (Math.random() * (top + 1)) << 0;
tmp = array[cur]; array[cur] = array[top]; array[top] = tmp;
}
return array;
}
Результаты теста: http://jsperf.com/optimized-fisher-yates
Я думаю, что это хорошо для случаев, когда вы не разборчивы в распространении и хотите, чтобы исходный код был небольшим.
В JavaScript (где источник передается постоянно), small влияет на стоимость полосы пропускания.
Нет, это неправильно. Как отмечалось в других ответах, это приведет к неравномерному перемешиванию, и качество перемешивания также будет зависеть от того, какой алгоритм сортировки использует браузер.
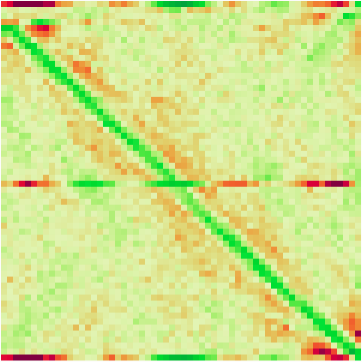
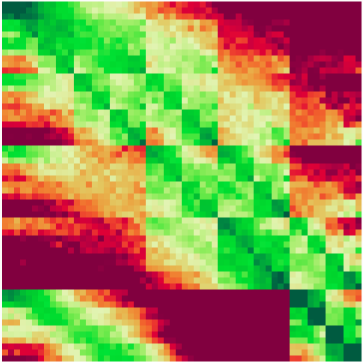
Это может показаться вам не таким уж плохим, потому что даже если теоретически распределение неравномерно, на практике оно, вероятно, почти однородно, верно? Ну нет , даже не близко. На следующих диаграммах показаны тепловые карты того, к каким индексам перетасовывается каждый элемент в Chrome и Firefox соответственно: если пиксель ( i , j ) зеленый, это означает, что элемент с индексом i слишком часто перетасовывается к индексу j , а если он красный, то он там перемешивается слишком редко.
Эти скриншоты взяты со страницы Майка Бостока на эту тему.
Как видите, перетасовка с использованием случайного компаратора сильно искажена в Chrome и тем более в Firefox. В частности, у обоих много зеленого цвета по диагонали, а это означает, что слишком много элементов «перемешиваются» где-то очень близко к тому месту, где они были в исходной последовательности. Для сравнения, аналогичная диаграмма для беспристрастной перетасовки (например, с использованием алгоритма Фишера-Йейтса ) была бы бледно-желтой с небольшим количеством случайного шума.
Прошло четыре года, но я хотел бы отметить, что метод случайного сравнения не будет правильно распределен, независимо от того, какой алгоритм сортировки вы используете.
Доказательство:
- Для массива
nэлементы, там точноn!перестановки (то есть возможные тасования). - Каждое сравнение в случайном порядке - это выбор между двумя наборами перестановок. Для случайного компаратора есть шанс 1/2 выбора каждого набора.
- Таким образом, для каждой перестановки p вероятность оказаться с перестановкой p является дробью со знаменателем 2^k (для некоторого k), поскольку она является суммой таких дробей (например, 1/8 + 1/16 = 3/16).
- Для n = 3 существует шесть одинаково вероятных перестановок. Таким образом, вероятность каждой перестановки равна 1/6. 1/6 не может быть выражена в виде дроби со степенью 2 в качестве знаменателя.
- Поэтому сортировка монетами никогда не приведет к справедливому распределению перемешиваний.
Единственные размеры, которые могут быть правильно распределены, это n=0,1,2.
В качестве упражнения попробуйте нарисовать дерево решений различных алгоритмов сортировки для n=3.
В доказательстве есть пробел: если алгоритм сортировки зависит от согласованности компаратора и имеет неограниченное время выполнения с несовместимым компаратором, он может иметь бесконечную сумму вероятностей, которую можно добавить до 1/6, даже если каждый знаменатель в сумме является степенью 2. Попытайтесь найти один.
Кроме того, если у компаратора есть фиксированная вероятность дать любой ответ (например, (Math.random() < P)*2 - 1для постоянного P), приведенное выше доказательство выполнено. Если компаратор вместо этого изменяет свои шансы на основе предыдущих ответов, возможно, будет возможно получить достоверные результаты. Поиск такого компаратора для данного алгоритма сортировки может быть исследовательской работой.
Это взлом, конечно. На практике алгоритм с бесконечной петлей маловероятен. Если вы сортируете объекты, вы можете перебрать массив координат и сделать что-то вроде:
for (var i = 0; i < coords.length; i++)
coords[i].sortValue = Math.random();
coords.sort(useSortValue)
function useSortValue(a, b)
{
return a.sortValue - b.sortValue;
}
(а затем повторите их снова, чтобы удалить sortValue)
Все еще взломать хотя. Если вы хотите сделать это красиво, вы должны сделать это трудным путем:)
Если вы используете D3, есть встроенная функция тасования (с использованием Fisher-Yates):
var days = ['Lundi','Mardi','Mercredi','Jeudi','Vendredi','Samedi','Dimanche'];
d3.shuffle(days);
И вот Майк подробно расскажет об этом:
Можете ли вы использовать функцию Array.sort() для перемешивания массива - да.
Являются ли результаты достаточно случайными - вероятно, нет. Я использовал этот JavaScript для тестирования:
var array = ["a", "b", "c", "d", "e"];
var stats = {};
for (var i = 0; i < array.length; i++) {
stats[array[i]] = [];
for (var j = 0; j < array.length; j++) {
stats[array[i]][j] = 0;
}
}
//stats = {
// a: [0, 0, 0, ...]
// b: [0, 0, 0, ...]
// c: [0, 0, 0, ...]
// ...
// ...
//}
for (var i = 0; i < 100; i++) {
var clone = array.slice(0);
clone.sort(function() {
return Math.random() - 0.5;
});
for (var j = 0; j < clone.length; j++) {
stats[clone[j]][j]++;
}
}
for (var i in stats) {
console.log(i, stats[i]);
}
Образец вывода:
a [29, 38, 20, 6, 7]
b [29, 33, 22, 11, 5]
c [17, 14, 32, 17, 20]
d [16, 9, 17, 35, 23]
e [ 9, 6, 9, 31, 45]
В идеале, количество должно быть равномерно распределено (для приведенного выше примера все значения должны быть около 20). Но это не так. По-видимому, распределение зависит от того, какой алгоритм сортировки реализован браузером и как он итерирует элементы массива для сортировки.
Более глубокое понимание предоставляется в этой статье:
Array.sort() не должен использоваться для перемешивания массива
Вот подход, который использует один массив:
Основная логика:
Код:
for(i=a.length;i--;) a.push(a.splice(Math.floor(Math.random() * (i + 1)),1)[0]);
В этом нет ничего плохого.
Функция, которую вы передаете.sort(), обычно выглядит примерно так:
функция sortingFunc (первая, вторая)
{
// пример:
вернуть первое - второе;
}Ваша задача в sortingFunc - вернуть:
- отрицательное число, если первое идет раньше второго
- положительное число, если первое должно идти после второго
- и 0, если они полностью равны
Вышеупомянутая функция сортировки упорядочивает вещи.
Если вы возвращаете "+" и "+" случайным образом, как и у вас, вы получаете случайный порядок.
Как в MySQL:
SELECT * из таблицы ORDER BY rand()