Печать круга ascii + выпуск топоров

Question

Эта программа печатает круг в декартовой плоскости.

Входные данные: радиус, координаты центра круга (cx,cy) и символ, которым мы хотим напечатать круг.

Если точки круга перекрываются с осями, точки имеют приоритет. Я написал условие для печати осей в методе drawCircle, но изображение искажается...

Что-то ускользает от меня... может кто-нибудь помочь мне найти мою ошибку?

Вот вся моя программа (метод, который имеет проблемы, последний, drawCircle):

public class Circle {

public static void main (String[] args){

  System.out.println(onCircle(1,2,3,4,5));

  drawCircle(1,3,3,'*');
  drawCircle(3,3,3,'*');
  drawCircle(5,10,12,'*');

}
//Question 1A  
public static boolean onCircle (int radius, int cx, int cy, int x, int y){
  //default answer is false, but if the inequality holds then it is set to true 
  boolean isDrawn = false;
    if(Math.pow(radius,2)<=(Math.pow((x-cx),2)+Math.pow((y-cy),2)) &&  (Math.pow((x-cx),2)+Math.pow((y-cy),2))<=(Math.pow(radius,2)+1)){
      isDrawn = true; 
    }
  return isDrawn;
}

//Question 1B
public static void verifyInput (int radius, int cx, int cy){
  //if radius is negative, display error message
  if (radius<=0){
    throw new IllegalArgumentException(" The radius of the circle must be a positive number.");
  }
  //if the center of the circle with radius 'radius' causes the circle to 'overflow' into other quadrants
  //, display error message
  if ((cx-radius)<0 || (cy-radius)<0){
    throw new IllegalArgumentException("the circle with requested parameters does not fit in the quadrant." 
                                         +"Consider moving the center of the circle further from the axes."); 
  }
}

//Question 1C
public static void drawCircle (int radius, int cx, int cy, char symbol){
  verifyInput(radius,cx,cy);

  //set the values for extension of the axes (aka how long are they)
  int xMax = cx+radius+1;
  int yMax = cy+radius+1;

  for(int j=yMax; j>=0; j--){
    for(int i=0; i<=xMax; i++){

      //set of if-block to print the axes
      if (i == 0 && j == 0){
        System.out.print('+');
      }
      else if(i == 0){
        if (j == yMax){
          System.out.print('^'); 
        }  
        if(j != yMax && onCircle(radius,cx,cy,i,j)==false){
          System.out.print('|');
        }
      }

      else if(j == 0){
        if(i == xMax){
          System.out.print('>');
        }
        if(i != xMax && onCircle(radius,cx,cy,i,j) == false){
          System.out.print('-');
        }
      }

      //if block to print the circle
      //verify for each coordinate (i,j) in the quadrant if they are on circle
      //if =true print symbol, if =false print empty character
      if(onCircle(radius,cx,cy,i,j)==true){
        System.out.print(symbol);
      }
      else{
        System.out.print(' ');
      }

    }
    System.out.println();

   }  
 }
}

Вот что я получаю:

Как вы можете видеть на картинке, 1-й и 3-й круги в порядке, но тот, который перекрывается с осями, искажается

Answer 1

Вам не хватает 3 операторов продолжения: посмотрите эту исправленную версию вашего метода drawCircle:

public static void drawCircle (int radius, int cx, int cy, char symbol){
  verifyInput(radius,cx,cy);

  //set the values for extension of the axes (aka how long are they)
  int xMax = cx+radius+1;
  int yMax = cy+radius+1;

 for(int j=yMax; j>=0; j--){
   for(int i=0; i<=xMax; i++){

  //set of if-block to print the axes
  if (i == 0 && j == 0){
    System.out.print('+');
    continue;
  }
  else if(i == 0){
    if (j == yMax){
      System.out.print('^'); 
    }  
    if(j != yMax && onCircle(radius,cx,cy,i,j)==false){
      System.out.print('|');
      continue;
    }
  }

  else if(j == 0){
    if(i == xMax){
      System.out.print('>');
    }
    if(i != xMax && onCircle(radius,cx,cy,i,j) == false){
      System.out.print('-');
      continue;
    }
  }

  //if block to print the circle
  //verify for each coordinate (i,j) in the quadrant if they are on circle
  //if =true print symbol, if =false print empty character
  if(onCircle(radius,cx,cy,i,j)==true){
    System.out.print(symbol);
  }
  else{
    System.out.print(' ');
  }

}
System.out.println();

}  
}

Answer 2

Общее уравнение круга с центром в начале координат:

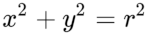
В Java это можно реализовать так:

      i*i + j*j == r*r

Но в случае целочисленной системы координат вы должны как-то округлить это уравнение, чтобы все точки круга отражались в этой системе координат:

      (int) Math.sqrt(i*i + j*j) == r

Если r=8, то круг и оси выглядят так:

      r=8
        * * * * * * * * *         
      * *       *       * *       
    *           *           *     
  *             *             *   
* *             *             * * 
*               *               * 
*               *               * 
*               *               * 
* * * * * * * * * * * * * * * * * 
*               *               * 
*               *               * 
*               *               * 
* *             *             * * 
  *             *             *   
    *           *           *     
      * *       *       * *       
        * * * * * * * * *         

Попробуйте онлайн!

      int r = 8;
System.out.println("r=" + 8);
IntStream.rangeClosed(-r, r)
        .map(i -> i * i)
        .peek(i2 -> IntStream.rangeClosed(-r, r)
                .map(j -> j * j)
                .mapToObj(j2 -> i2 == 0 || j2 == 0 ||
                        (int) Math.sqrt(i2 + j2) == r ?
                        "* " : "  ")
                .forEach(System.out::print))
        .forEach(i2 -> System.out.println());

---

^{См. Также: Распечатайте звезду ASCII в java}

Answer 3

На самом деле при отладке ваши методы onCircle получают значения x=0 и y=4, cx=3, cy=3:

У тебя есть:

Math.pow(radius=3,2) = 9
Math.pow((x - cx), 2) = 9
Math.pow((y - cy), 2) = 1

следовательно

Math.pow(radius, 2) <= Math.pow((x - cx), 2) + Math.pow((y - cy), 2)

возвращает истину

Затем:

(Math.pow((x-cx),2) = 9
Math.pow((y-cy),2)) = 1
(Math.pow(radius,2)+1)) = 10

таким образом

(Math.pow((x-cx),2)+Math.pow((y-cy),2)) <= (Math.pow(radius,2)+1)) 

возвращает также верно

Таким образом, onCircle(radius,cx,cy,i,j) возвращает true для этой координаты.

И именно поэтому вы получаете ваш символ. Вам нужно улучшить свой алгоритм!