Как интерполировать координаты ECEF на эллипсоиде WGS84

Question

Существует ли прямой метод (не предусматривающий преобразование координат в широту / долготу) для интерполяции между двумя координатами ECEF (xyz), чтобы интерполированная точка находилась на эллипсоиде WGS84. Исходные 2 точки рассчитываются по геодезическим координатам.

Интерполяция на сфере кажется очевидной, но я не могу найти решение для эллипсоида.

Заранее спасибо.

Answer 1

Допустим, вы получили 2 балла p0(x,y,z) а также p1(x,y,z) и хочу интерполировать некоторые p(t) где t=<0.0,1.0> между двумя.

вы можете:

1. измените масштаб своего эллипсоида на сферу

   просто так:

   const double mz=6378137.00000/6356752.31414; // [m] equatoreal/polar radius of Earth
   p0.z*=mz;
   p1.z*=mz;
   

   теперь вы получили декартовы координаты, относящиеся к сферической модели Земли.

2. интерполировать

   простая линейная интерполяция сделает

   p(t) = p0+(p1-p0)*t
   

   но, конечно, вы также должны нормализовать кривизну земли так:

   r0 = |p0|
   r1 = |p1|
   
   p(t) = p0+(p1-p0)*t
   r(t) = r0+(r1-r0)*t
   
   p(t)*=r/|p(t)|
   

   где |p0| означает длину вектора p0,

3. перемасштабировать обратно на эллипсоид

   разделив с тем же значением

   p(t).z/=mz
   

Это просто и дешево, но интерполированный путь не будет иметь линейного масштаба времени.

Вот пример C++:

void XYZ_interpolate(double *pt,double *p0,double *p1,double t)
    {
    const double  mz=6378137.00000/6356752.31414;
    const double _mz=6356752.31414/6378137.00000;
    double p[3],r,r0,r1;
    // compute spherical radiuses of input points
    r0=sqrt((p0[0]*p0[0])+(p0[1]*p0[1])+(p0[2]*p0[2]*mz*mz));
    r1=sqrt((p1[0]*p1[0])+(p1[1]*p1[1])+(p1[2]*p1[2]*mz*mz));
    // linear interpolation
    r   = r0   +(r1   -r0   )*t;
    p[0]= p0[0]+(p1[0]-p0[0])*t;
    p[1]= p0[1]+(p1[1]-p0[1])*t;
    p[2]=(p0[2]+(p1[2]-p0[2])*t)*mz;
    // correct radius and rescale back
    r/=sqrt((p[0]*p[0])+(p[1]*p[1])+(p[2]*p[2]));
    pt[0]=p[0]*r;
    pt[1]=p[1]*r;
    pt[2]=p[2]*r*_mz;
    }

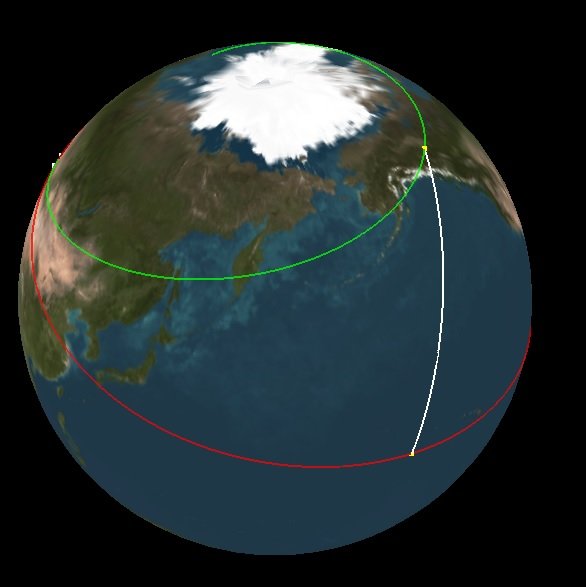
И предварительный просмотр:

Желтые квадраты используются p0,p1 Декартовы координаты, белая кривая - это интерполированный путь, где t=<0.0,1.0>...