Построение полиномиальной логистической регрессии VGLM с 95% ДИ
Я хотел бы построить прогнозируемые значения полиномиальной логистической регрессии, полученные из vglm() функция в пакете VGAM.
Важно, чтобы я использовал VGAM, потому что я пытаюсь повторить анализ коллеги, проведенный в Stata, который я достиг с помощью этой функции / пакета.
Подмножество данных:
structure(list(
caretime3 = c(0, 2, 2, 0, 0, 2, 1, 1, 0, 2, 2, 0, 1, 0, 1, 1, 2, 1, 2, 2, 2, 1, 1, 0, 1, 1, 2, 2, 0, 1),
pmt05allz = c(0.1315678358078, 2.57276844978333, -0.86949759721756, -0.844452261924744, -0.48639452457428, 1.87834203243256, -0.988184869289398, -1.02298593521118, 0.570109307765961, 1.00886857509613, -0.972711682319641, -0.713021039962769, -0.70054304599762, 1.02071666717529, -0.571928858757019, -0.786627769470215, -0.628270447254181, 1.76193022727966, 0.75188934803009, 1.22556257247925, -0.205045282840729, -0.163282126188278, -0.149484217166901, -0.710245132446289, -0.631508588790894, -0.372817307710648, -0.0988877564668655, -0.28418955206871, -0.386095404624939, -1.8762229681015),
arz = c(0.283046782016754, 0.283046782016754, -0.00598874036222696, -0.00598874036222696, 0.572082281112671, 0.283046782016754, 0.283046782016754, -0.295024245977402, -0.295024245977402, -0.584059774875641, 1.43918883800507, 0.861117839813232, -0.00598874036222696,-0.584059774875641, 0.283046782016754, -1.16213083267212, -0.584059774875641, -0.295024245977402, 1.1501532793045, -0.00598874036222696, -1.74020183086395,4.90761518478394, 1.43918883800507, -0.873095273971558, -0.295024245977402, 0.283046782016754, 1.1501532793045, 0.861117839813232, -0.295024245977402, 1.1501532793045),
arlevel = structure(c(2L, 2L, 2L, 2L, 3L, 2L, 2L, 1L, 1L, 1L, 3L, 3L, 2L, 1L, 2L, 1L, 1L, 1L, 3L, 2L, 1L, 3L, 3L, 1L, 1L, 2L, 3L, 3L, 1L, 3L), .Label = c("short", "medium", "long"), class = "factor")), .Names = c("caretime3", "pmt05allz", "arz", "arlevel"), row.names = c(1566L, 1142L, 1637L, 574L, 507L, 1500L, 1393L, 1609L, 877L, 753L, 895L, 1608L, 1827L, 1342L, 1435L, 451L, 1606L, 368L, 848L, 1829L, 395L, 81L, 1021L, 87L, 1388L, 1765L, 491L, 29L, 5L, 1020L), class = "data.frame")
Модель выглядит следующим образом:
ctime.ml2 <-vglm(caretime3~ pmt05allz*arlevel,
family = multinomial(refLevel = 1), data = CAG.sort)
Результат выглядит так:
Call:
vglm(formula = caretime3 ~ pmt05allz * arz,
family = multinomial(refLevel = 1), data = CAG.sort)
Pearson residuals:
Min 1Q Median 3Q Max
log(mu[,2]/mu[,1]) -1.771 -0.7532 -0.3770 1.089 2.177
log(mu[,3]/mu[,1]) -1.572 -0.8929 -0.3578 1.288 1.890
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept):1 0.24763 0.16787 1.475 0.1402
(Intercept):2 0.12888 0.17101 0.754 0.4511
pmt05allz:1 -0.28920 0.16643 -1.738 0.0823 .
pmt05allz:2 -0.13245 0.15691 -0.844 0.3986
arz:1 0.40889 0.18664 2.191 0.0285 *
arz:2 -0.08447 0.19705 -0.429 0.6681
pmt05allz:arz:1 0.56149 0.24221 2.318 0.0204 *
pmt05allz:arz:2 0.39024 0.22904 1.704 0.0884 .
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Number of linear predictors: 2
Names of linear predictors: log(mu[,2]/mu[,1]), log(mu[,3]/mu[,1])
Dispersion Parameter for multinomial family: 1
Residual deviance: 499.5317 on 466 degrees of freedom
Log-likelihood: -249.7659 on 466 degrees of freedom
Number of iterations: 4
С использованием predict(m1, newdata) Функция предоставляет мне две колонки.
log(mu[,2]/mu[,1]) log(mu[,3]/mu[,1])
1 1.837926621 1.6387672851
2 1.784309766 1.5924054498
3 1.730692911 1.5460436146
4 1.677076056 1.4996817793
5 1.623459202 1.4533199440
Q1. Эти два столбца являются линейными предсказаниями для каждого из двух уровней относительно контрольного уровня (reflevel = 1), верно?
Напротив, используя predict(m1, newdata = newdata, type = "response") предоставляет мне три столбца (0, 1 и 2).
0 1 2
1 0.08043554 0.50541645 0.41414801
2 0.08423871 0.50168094 0.41408035
3 0.08820341 0.49786976 0.41392683
4 0.09233480 0.49398103 0.41368418
5 0.09663804 0.49001289 0.41334907
...
Q2. Каковы эти три столбца? Какие из них соответствуют приведенным выше сравнениям (уровни контрастности 2 и 3 - уровень 1)?
Q3. Могу ли я получить стандартные ошибки (95% ДИ) для прогнозируемых значений в переменной отклика, которые я затем смогу построить? Если так, то как?
Резюме: из полиномиальной логистической регрессии я пытаюсь получить что-то вроде этого из Stata: 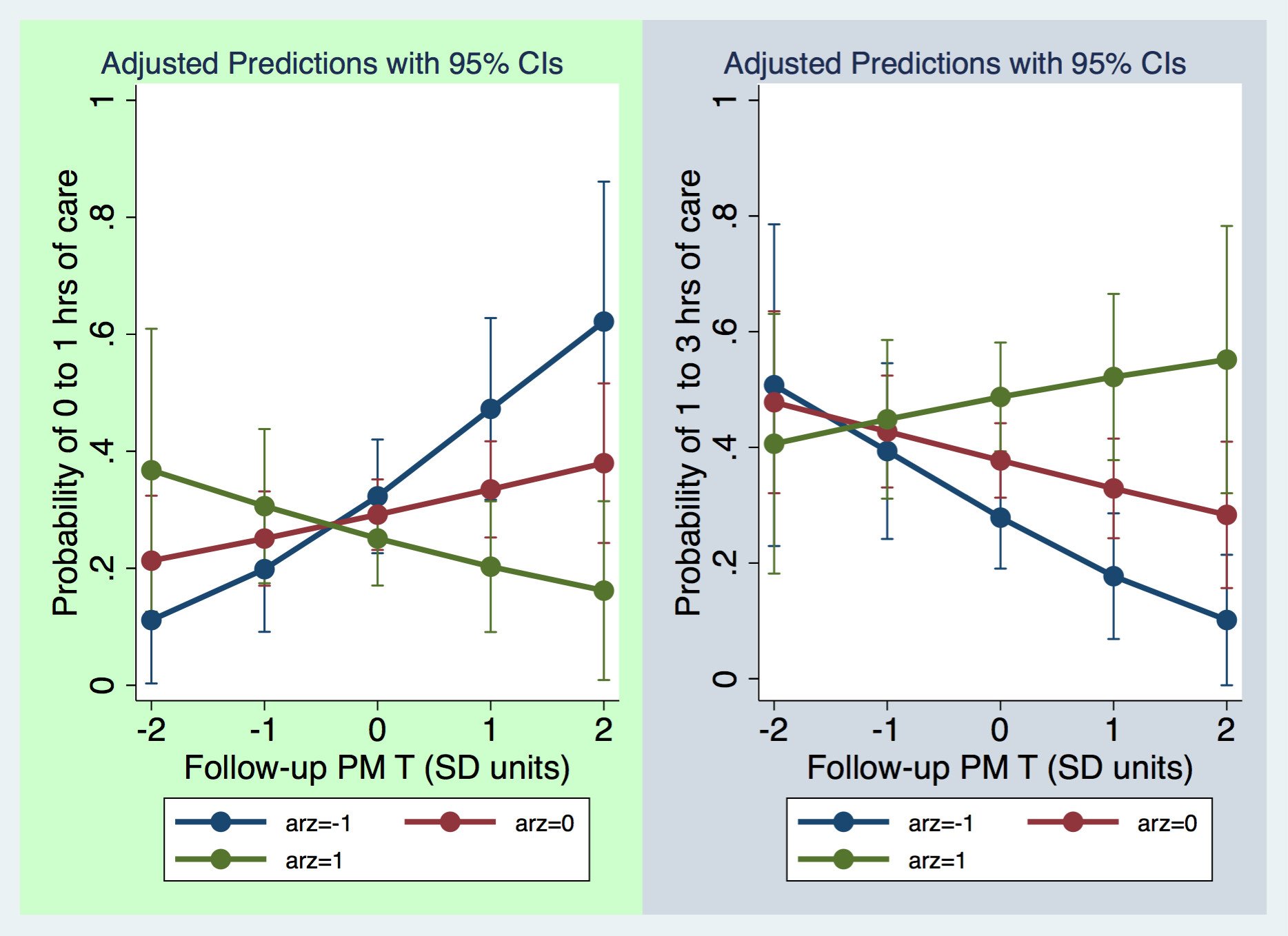
Это на самом деле выглядит примерно так: 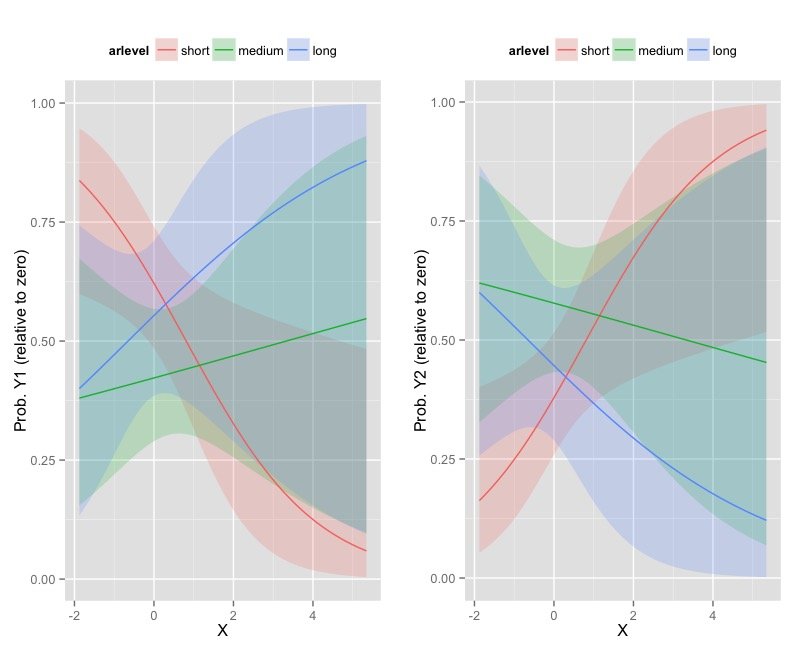
В основном, я хочу, чтобы прогнозируемая переменная ответа (caretime3) одной из переменных предиктора x (pmt05allz) в диапазоне х2 (arz), но в конечном итоге для визуализации сгруппированы по arz (arlevel).