Определить все локальные экстремумы сглаженного сплайна с помощью функции R "smooth.spline"

Question

У меня есть двумерный набор данных.

Я использую R smooth.spline функция, чтобы сгладить мой график точек, следуя примеру из этой статьи:

https://stat.ethz.ch/R-manual/R-devel/library/stats/html/predict.smooth.spline.html

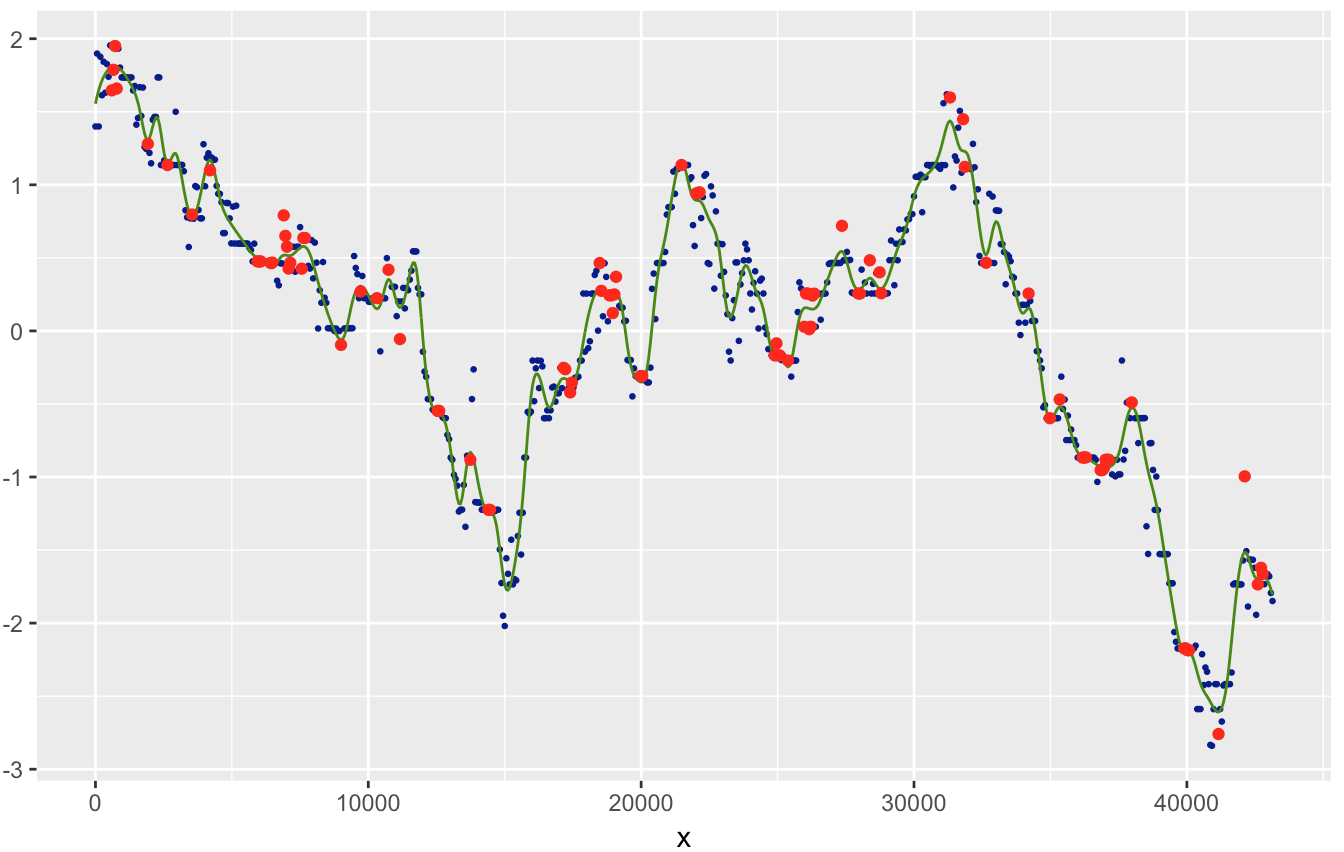
Так что я получаю сплайн-график, похожий на зеленую линию на этой картинке

Я хотел бы знать X значения, где первая производная сглаживающего сплайна равна нулю (чтобы определить точный минимум или максимум).

Моя проблема в том, что мой начальный набор данных (или набор данных, который я мог бы автоматически сгенерировать) для подачи в predict() функция не содержит такого точного X значения, которые соответствуют экстремумам сплайна сглаживания.

Как я могу найти такой X ценности?

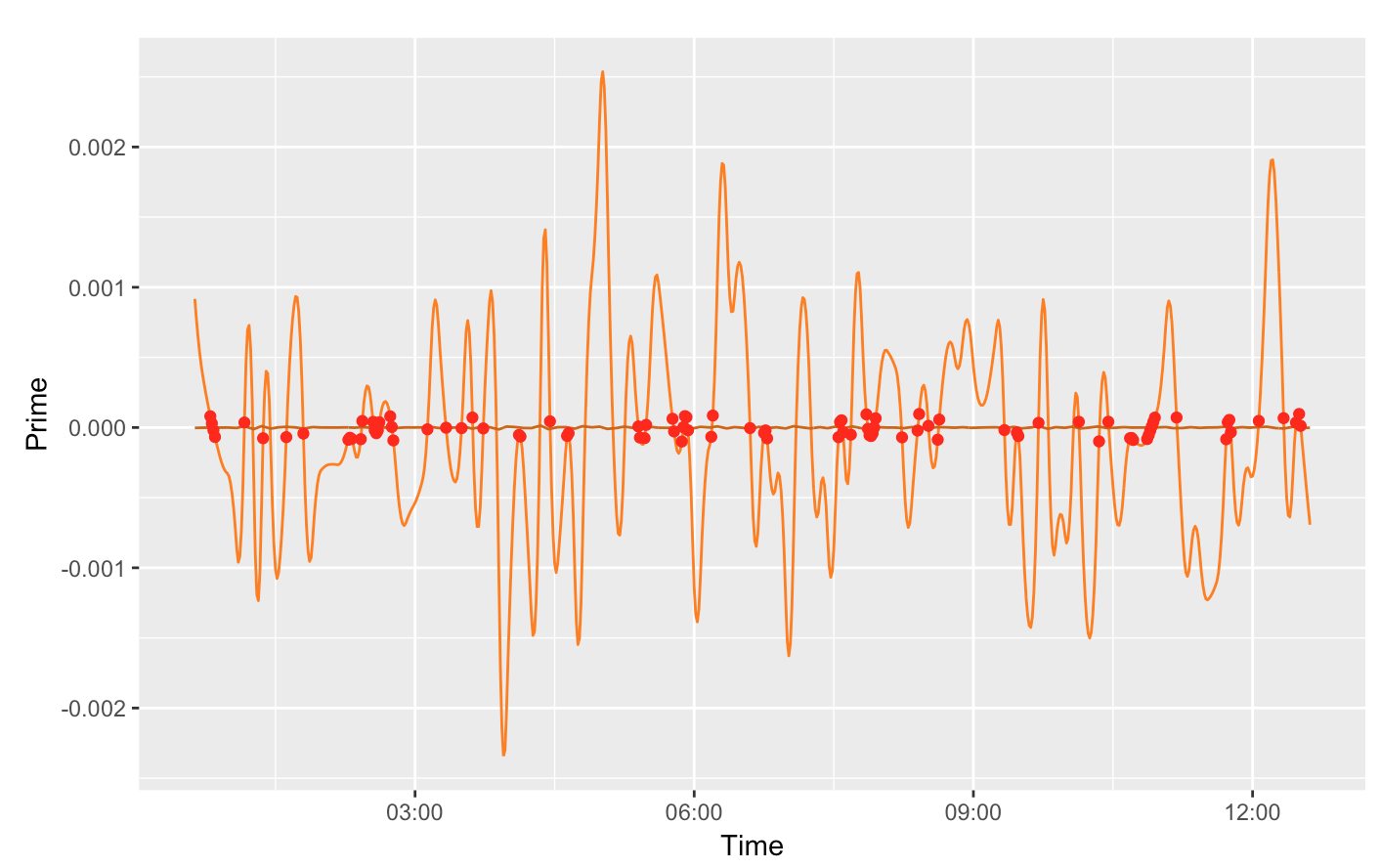
Вот изображение первой производной зеленой сплайновой линии выше

Но точные координаты X экстремумов все еще не точны.

Мой примерный R скрипт для генерации картинок выглядит следующим образом

sp1 <- smooth.spline(df)

pred.prime <- predict(sp1, deriv=1)
pred.second <- predict(sp1, deriv=2)

d1 <- data.frame(pred.prime)
d2 <- data.frame(pred.second)

dfMinimums <- d1[abs(d1$y) < 1e-4, c('x','y')]

Answer 1

Я думаю, что здесь есть две проблемы.

1. Вы используете исходные значения x, и они расположены слишком далеко друг от друга.
2. Из-за большого расстояния между х, ваш порог для того, где вы считаете производную "достаточно близкой к нулю", слишком высок.

Вот, в основном, ваш код, но со многими другими значениями x и требующими меньших производных. Поскольку вы не предоставляете никаких данных, я сделал грубое приближение к нему, которого должно хватить для иллюстрации.

## Coarse approximation of your data
x = runif(300, 0,45000)
y = sin(x/5000) + sin(x/950)/4 + rnorm(300, 0,0.05) 
df = data.frame(x,y)
sp1 <- smooth.spline(df)

Сплайн код

Sx = seq(0,45000,10)
pred.spline <- predict(sp1, Sx)
d0 <- data.frame(pred.spline)
pred.prime <- predict(sp1, Sx, deriv=1)
d1 <- data.frame(pred.prime)

Mins = which(abs(d1$y) < mean(abs(d1$y))/150)

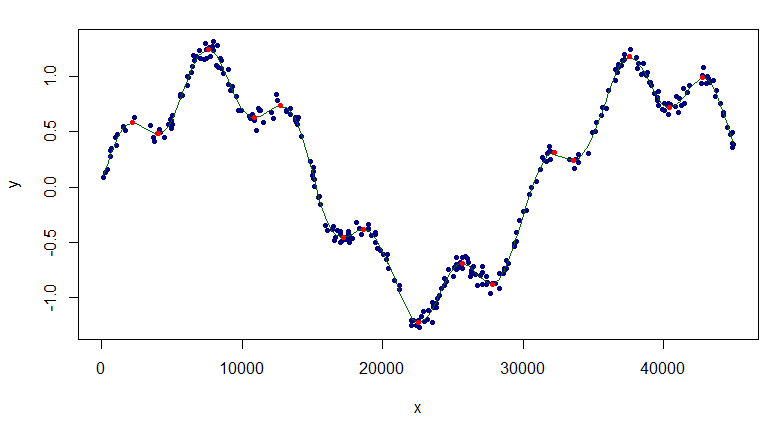
plot(df, pch=20, col="navy")
lines(sp1, col="darkgreen")
points(d0[Mins,], pch=20, col="red")

Экстремумы выглядят довольно хорошо.

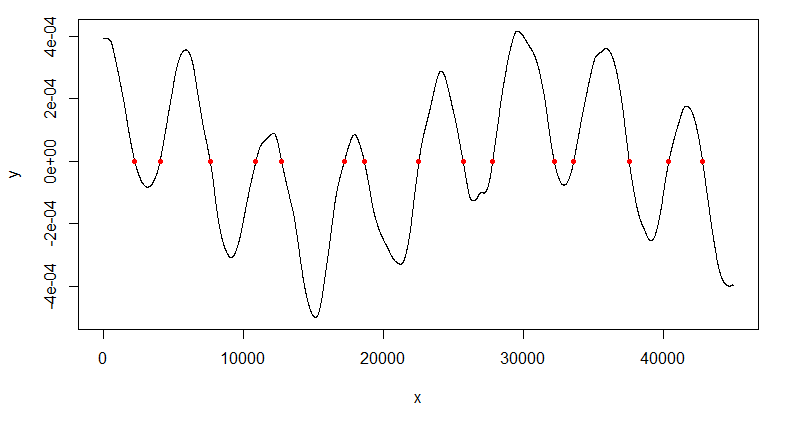
plot(d1, type="l")
points(d1[Mins,], pch=20, col="red")

Идентифицированные точки выглядят как нули производной.

Answer 2

Вы можете использовать мой пакет R SplinesUtils: https://github.com/ZheyuanLi/SplinesUtils, который может быть установлен

devtools::install_github("ZheyuanLi/SplinesUtils")

Используемая функция SmoothSplinesAsPiecePoly а также solve, Я просто буду использовать пример в документации.

library(SplinesUtils)

## a toy dataset
set.seed(0)
x <- 1:100 + runif(100, -0.1, 0.1)
y <- poly(x, 9) %*% rnorm(9)
y <- y + rnorm(length(y), 0, 0.2 * sd(y))

## fit a smoothing spline
sm <- smooth.spline(x, y)

## coerce "smooth.spline" object to "PiecePoly" object
oo <- SmoothSplineAsPiecePoly(sm)

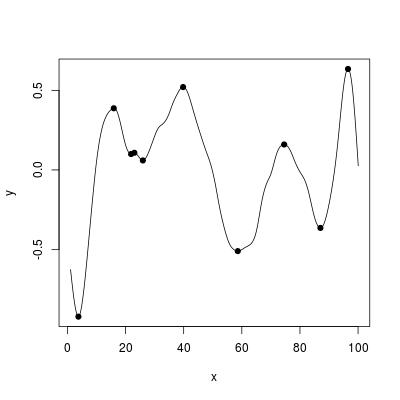
## plot the spline
plot(oo)

## find all stationary / saddle points
xs <- solve(oo, deriv = 1)
#[1]  3.791103 15.957159 21.918534 23.034192 25.958486 39.799999 58.627431
#[8] 74.583000 87.049227 96.544430

## predict the "PiecePoly" at stationary / saddle points
ys <- predict(oo, xs)
#[1] -0.92224176  0.38751847  0.09951236  0.10764884  0.05960727  0.52068566
#[7] -0.51029209  0.15989592 -0.36464409  0.63471723
points(xs, ys, pch = 19)

Answer 3

Я обнаружил одну оговорку в реализации @G5W, которая иногда возвращает несколько записей, близких к экстремальным, вместо одной. На диаграмме их не видно, поскольку все они эффективно попадают в одну точку.

Следующий фрагмент отсюда отфильтровывает отдельные точки экстремумов с минимальным значением первой производной:

library(tidyverse)
df2 <- df  %>%
  group_by(round(y, 4)) %>% 
  filter(abs(d1) == min(abs(d1))) %>% 
  ungroup() %>% 
  select(-5)