Найти угловые точки четырехугольника из набора точек

Question

Я пытаюсь получить угловые точки четырехугольника из набора точек.

• Набор точек упорядочен и описывает контур
• Иногда контур имеет некоторый шум (см. 2-е изображение)
• Обыскиваемые угловые точки не обязательно должны быть точками из заданного набора точек (см. Третий рисунок внизу слева)
• Найденные угловые точки описывают выпуклый четырехугольник, не обязательно прямоугольник

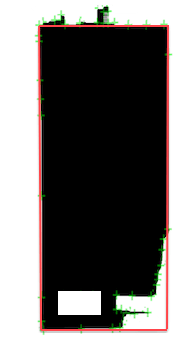
Второе изображение немного экстремально, но "качество" моего набора точек лежало между кулаком и вторым изображением.

Сначала я подумал о создании гистограммы длиной более 1-360°, описывают два следующих пункта. Четыре самых высоких пика будут описывать длину каждой линии. Но с этим я теряю точки ордера, просто знайте о степени и длине или линии и не знаете, к какой позиции принадлежит линия.

Затем я подумал о слиянии двух следующих строк, если они имеют более или менее одинаковую степень, но я не знаю, как справиться с шумом здесь или предсказать угол.

Кто-нибудь знает алгоритм, который решает эту проблему или что-то подобное?

Answer 1

Вы можете рассматривать это как проблему кластеризации, когда "центры" кластера на самом деле являются прямыми. Для вычисления кластеризации вы можете использовать алгоритм k-средних:

1. Выберите 4 случайных пары точек. Подгоните линию к каждому, чтобы у вас было 4 линии, проходящие через облако точек.
2. Повторяйте, пока решение, кажется, не сошлось:
   1. Для каждой из точек вычислите расстояние до каждой из 4 линий.
   2. Назначьте точку ведру, которое соответствует линии, к которой оно ближе всего.
   3. Установите 4 новые линии на точки в каждом из 4 сегментов (вы можете использовать линейную регрессию или SVD)

Чтобы улучшить первый шаг, вы можете взять гистограмму по углам и назначить каждую точку в начале, соответствующем ближайшему пику. Затем поместите строки в четыре сегмента и начните итерацию.

Вы также можете рассматривать это как проблему оптимизации: выберите 4 точки, чтобы область разницы (белая область внутри и черная область вне четырехугольника) была как можно меньше. Общие алгоритмы оптимизации, вероятно, работают, но для их ускорения необходим разумный алгоритм для вычисления областей.