Решите логнормальное уравнение для мю и сигмы при фиксированных значениях y и x в Matlab
У меня есть логнормальное уравнение:
y = 1 / (3,14*x*sig)*exp(-(log(x)-mu)^2/(2*sig^2))
и для фиксированной
у = а
х = б
Мне нужно найти значения мю и сиг. Я могу установить му в Matlab, как:
mu = [0 1 1,1 1,2...]
и найти все значения, соответствующие значениям сиг, но я не могу сделать это с помощью решения или подпрограмм. Любые идеи, пожалуйста???
Спасибо!
1 ответ
Вот подтверждение концепции для использования fzero численно искать sigma(x,y,mu) функция.
Если у вас есть x,y исправлено, вы можете установить
mu = 1; %or whatever
myfun = @(sig) y-1./(3.14*x*sig).*exp(-(log(x)-mu)^2./(2*sig.^2)); %x,y,mu from workspace
sigma = fzero(myfun,1);
Это решит уравнение
y-1/(3.14*x*sig)*exp(-(log(x)-mu)^2/(2*sig^2))==0
за sig начиная с sig==1 и вернуть его в sigma,
Вы можете обобщить это, чтобы получить функцию mu:
myfun2 = @(mu,sig) y-1./(3.14*x*sig).*exp(-(log(x)-mu).^2./(2*sig.^2));
sigmafun=@(mu) fzero(@(sig)myfun2(mu,sig),1);
затем sigmafun даст вам sigma для каждого значения mu Вы положили в это. Параметры x а также y предполагается установить перед первым объявлением анонимной функции.
Или вы можете получить действительно общие и определить
myfun3 = @(x,y,mu,sig) y-1./(3.14*x*sig).*exp(-(log(x)-mu).^2./(2*sig.^2));
sigmafun2 = @(x,y,mu) fzero(@(sig)myfun3(x,y,mu,sig),1);
Основное отличие здесь в том, что x а также y питаются в функции sigmafun2 каждый раз, чтобы они могли измениться. В более ранних случаях значения x а также y были зафиксированы в анонимных функциях во время их определения, т.е. когда мы выпустили myfun = @(sig)..., В зависимости от ваших потребностей вы можете узнать, что вы хотите использовать.
В качестве доказательства концепции я не проверял, насколько хорошо она себя ведет в реальной проблеме. Вы должны определенно иметь первоначальное представление о том, какие параметры вы ожидаете, так как будет много случаев, когда нет решения, и fzero вернет NaN,
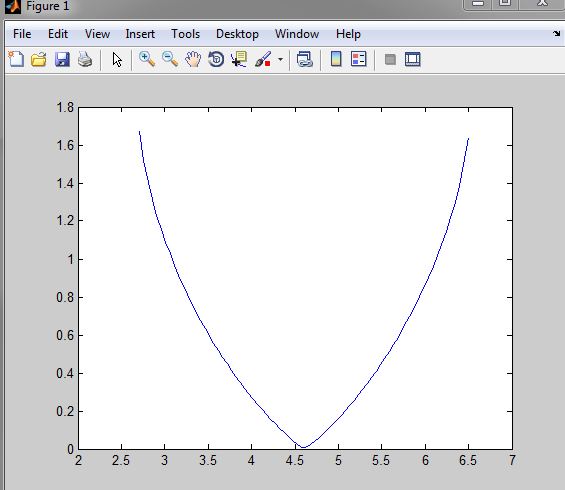
Обновление Оливер Амундсен: итоги sig(mu) функция с x=100, y=0.001 выглядит так: