Морфинг изображения с триангуляцией Делоне
Я разрабатываю простой алгоритм для преобразования двух изображений с использованием ключевых точек и триангуляции Делоне. Идея должна быть простой:
- выберите исходную контрольную точку
- выберите пункт назначения
- получить триангуляцию Делоне для исходного и конечного кадров
- для каждого пикселя в исходном изображении
- получить барицентрические координаты пикселя, связанные с исходным треугольником, в котором лежит пиксель
- получить барицентрические координаты пикселя, связанные с конечным треугольником, в котором находится пиксель
- используя соотношение Px = w1*v0x + w2*v1x + w3*v2x (то же самое для y и целевого пикселя), назначьте OUT[PdestX,PdestY] = IN[Px,Py].
Но это не работает X_X Это мой источник Matlab:
function out = myMorph(im1, p_source, p_dest, tri_source, tri_dest)
[h w] = size(im1);
%get single column vectors for source and destination image control points
Psource_x = p_source(:,1);
Psource_y = p_source(:,2);
Pdest_x = p_dest(:,1);
Pdest_y = p_dest(:,2);
%for each intermediate frame...
out = zeros(size(im1));
%get triangles. Each array is 3n x 2, where n is the number of triangles
triangles_source = [];
triangles_dest = [];
for i= 1 : size(tri_source,1)
triangle_s = getTriangle(Psource_x,Psource_y,tri_source,i);
triangle_d = getTriangle(Pdest_x,Pdest_y,tri_dest,i);
triangles_source = cat(1,triangles_source,triangle_s);
triangles_dest = cat(1,triangles_dest,triangle_d);
end
%iterate each pixel
for x=1:h
for y=1:w
%get the source and destination triangle for pixel [x y]
%source triangle
for t = 1 : 3 : size(triangles_source, 1)-2
[w1,w2,w3,inTriangle] = inTri(x,y, ...
triangles_source(t,1),triangles_source(t,2), ...
triangles_source(t+1,1),triangles_source(t+1,2), ...
triangles_source(t+2,1),triangles_source(t+2,2));
if(inTriangle == 1)
break; %point [x,y] must belong to one (and only) triangle
end
end
%source triangle
for k = 1 : 3 : size(triangles_dest, 1)-2
[w1d,w2d,w3d,inTriangleD] = inTri(x,y, ...
triangles_dest(k,1),triangles_dest(k,2), ...
triangles_dest(k+1,1),triangles_dest(k+1,2), ...
triangles_dest(k+2,1),triangles_dest(k+2,2));
if(inTriangleD == 1)
break;
end
end
v_source = [w1*triangles_source(t,1) + ...
w2*triangles_source(t+1,1) + ...
w3*triangles_source(t+2,1), ...
w1*triangles_source(t,2) + ...
w2*triangles_source(t+1,2) + ...
w3*triangles_source(t+2,2)];
v_dest = [w1d*triangles_dest(k,1) + ...
w2d*triangles_dest(k+1,1) + ...
w3d*triangles_dest(k+2,1),...
w1d*triangles_dest(k,2) + ...
w2d*triangles_dest(k+1,2) + ...
w3d*triangles_dest(k+2,2)];
if(inTriangle ~= 1 && inTriangleD ~= 1)
continue;
end
v_source = round(v_source);
v_dest = round(v_dest);
if(v_source(1)>0 && v_source(1) <= h && ...
v_source(2)>0 && v_source(2) <= w && ...
v_dest(1)>0 && v_dest(1) <= h && ...
v_dest(2)>0 && v_dest(2) <= w)
disp('pixel warped')
out(v_dest(1),v_dest(2)) = im1(v_source(1),v_source(2));
end
% else
% out(x,y) = im1(x,y);
end
end
Это служебная функция для получения контрольных точек
%Get control points used to morph im into another image
%im -> source image
%im2 -> destination image
%linesNum -> number of lines
function [P] = getControlPoints(im, controlPtsNum)
close all
P = zeros(controlPtsNum, 2);
%select lines from source image
figure;
imshow(im,[]);title('select control points')
for i=1 : controlPtsNum
%get source control point
[x,y] = ginput(1);
P(i,:) = [x,y];
hold on
plot(x,y,'o','Color','r');
hold off
end
%Get control points used to morph im into another image and do delaunay
%triangulation using the control points
%im -> source image
%im2 -> destination image
%controlPtsNum -> number of control points
function [P,tri] = getControlPointsAndTriangulate(im, controlPtsNum)
P = getControlPoints(im, controlPtsNum);
[h w] = size(im);
%Add corners to control points
P = cat(1, P, [1 1]);
P = cat(1, P, [w 1]);
P = cat(1, P, [1 h]);
P = cat(1, P, [w h]);
tri = delaunay(P(:,1),P(:,2));
hold on
triplot(tri,P(:,1),P(:,2))
hold on
и эта функция (я нашел в сети), проверяет, лежит ли точка в данном треугольнике, и возвращает значения u,v,w:
function [w1,w2,w3,r] = inTri(vx, vy, v0x, v0y, v1x, v1y, v2x, v2y)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% inTri checks whether input points (vx, vy) are in a triangle whose
% vertices are (v0x, v0y), (v1x, v1y) and (v2x, v2y) and returns the linear
% combination weight, i.e., vx = w1*v0x + w2*v1x + w3*v2x and
% vy = w1*v0y + w2*v1y + w3*v2y. If a point is in the triangle, the
% corresponding r will be 1 and otherwise 0.
%
% This function accepts multiple point inputs, e.g., for two points (1,2),
% (20,30), vx = (1, 20) and vy = (2, 30). In this case, w1, w2, w3 and r will
% be vectors. The function only accepts the vertices of one triangle.
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
v0x = repmat(v0x, size(vx,1), size(vx,2));
v0y = repmat(v0y, size(vx,1), size(vx,2));
v1x = repmat(v1x, size(vx,1), size(vx,2));
v1y = repmat(v1y, size(vx,1), size(vx,2));
v2x = repmat(v2x, size(vx,1), size(vx,2));
v2y = repmat(v2y, size(vx,1), size(vx,2));
w1 = ((vx-v2x).*(v1y-v2y) - (vy-v2y).*(v1x-v2x))./...
((v0x-v2x).*(v1y-v2y) - (v0y-v2y).*(v1x-v2x)+eps);
w2 = ((vx-v2x).*(v0y-v2y) - (vy-v2y).*(v0x-v2x))./...
((v1x-v2x).*(v0y-v2y) - (v1y-v2y).*(v0x-v2x)+eps);
w3 = 1 - w1 - w2;
r = (w1>=0) & (w2>=0) & (w3>=0) & (w1<=1) & (w2<=1) & (w3<=1);
Любое предложение? До свидания!
1 ответ
Я не могу воспроизвести ошибки в вашем коде, потому что у меня нет входного набора данных, однако, согласно вашему описанию, у вас может быть та же проблема, что и у меня, когда я вчера пытался изменить изображение с помощью триангуляции:
Количество треугольников в исходной триангуляции и в целевой триангуляции различно.
Это может быть вызвано тем, что вы описали в своих действиях:
- Выполните триангуляцию Делоне с контрольными точками источника, получите треугольную сетку
- Выполните триангуляцию Делоне с контрольными точками назначения, получите треугольную сетку
Триангуляция Делоне настолько умна, что она использует минимальное количество треугольников для триангуляции. Он не знает, что контрольные точки на шаге 2 "преобразованы" из контрольных точек на шаге 1. Таким образом, треугольные сетки из шагов 1 и 2 могут содержать различное количество треугольников! Вот пример и как решить проблему:
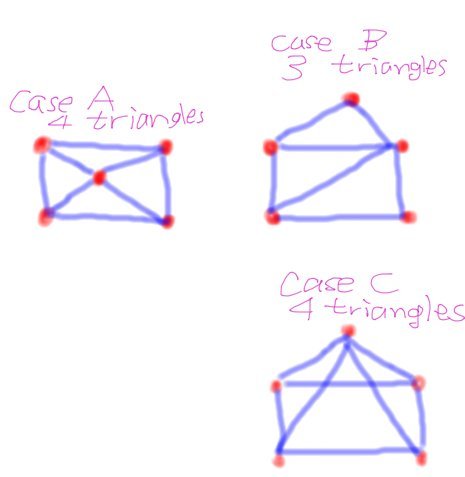
Допустим, вы создали 2 списка контрольных точек: "исходный CP" и "целевой CP". "CP источника" - красные точки в случае A. "CP пункта назначения" - красные точки в случаях B и C (они идентичны).
Случай A получается путем выполнения триангуляции Делоне над "источником CP".
Случай B получается путем выполнения триангуляции Делоне над "CP назначения".
Увидеть? Случай B содержит на 1 меньше треугольника, чем случай A!! Если это произойдет, вы не сможете трансформироваться, используя списки треугольников в триангуляции Делоне в случаях A и B.
Обходной путь - получить Случай C с тем же списком смежности и тем же числом треугольников, что и в случае A, тогда вы можете выполнить морфинг изображения с помощью метода аффинного преобразования парных треугольников в треугольники.
Случай C получается простым перемещением одной контрольной точки в случае A, но с сохранением того же списка смежности.
Конечно, перекрывающиеся треугольники теперь стали новой проблемой. Я думаю, что вы можете установить ограничения, такие как величина искажения, чтобы предотвратить наложение треугольников. Кроме того, тестовый код пересечения треугольников, который вы опубликовали, учитывает перекрывающиеся треугольники, возвращая идентификатор треугольника 1-го треугольника в списке, который пересекается с точкой запроса.
Таким образом, дело в том, что вам нужно выполнить триангуляцию Делоне только один раз для пары преобразования источник-назначение.
Надеюсь это поможет!