Как остановить случайную прогулку
plot(0:70,0:70, type="n", xlab="X", ylab="Y")
x<-40
y<-40
x2<-60
y2<-60
points(x, y, pch=16, col="red", cex=1.5)
points(x2, y2, pch=16, col="green", cex=1.5)
for (i in 1:10000){
xi<-sample(c(1,0,-1),1)
yi<-sample(c(1,0,-1),1)
x2i<-sample(c(1,0,-1),1)
y2i<-sample(c(1,0,-1),1)
lines(c(x,x+xi),c(y,y+yi))
lines(c(x2,x2+x2i),c(y2,y2+y2i), col="red")
x<-x+xi
y<-y+yi
x2<-x2+x2i
y2<-y2+y2i
if(x2==x && y==y2) {
break
}
}
У меня есть эта случайная прогулка с двумя линиями, и мне нужно, чтобы она остановилась, когда две линии встретятся.
Сначала я нарисовал пустой график и две начальные точки для линий. Затем у меня есть цикл for для перемещения линий, чтобы нарисовать их на графике и получить новые начальные точки для следующей итерации.
Я пытался остановить это, когда строки встречаются, используя: if(x2==x && y==y2) { break } но линии останавливаются, только если они находятся в одной и той же точке и в одно и то же время (на одной и той же итерации), и мне нужно, чтобы они останавливались, если одна из них пересекает другую. Если один пересекает какую-либо точку, то рисуйте для другой линии. Я думаю, что проблема в том, что уже нарисованные точки нигде не сохраняются, поэтому я не могу сравнить их с точками линий. Может быть, мне нужно сохранить точки из цикла? Кто-то знает, как это остановить?
1 ответ
N <- 10000
D <- 1
coef.1 <- matrix(NA,N,2)
coef.2 <- matrix(NA,N,2)
path.1 <- matrix(NA,N,2)
path.2 <- matrix(NA,N,2)
path.1[1,] <- c(40,40)
path.2[1,] <- c(60,60)
d.start <- sqrt(sum((path.1[1,]-path.2[1,])^2))
ch <- "."
set.seed(1)
system.time({
for (i in 2:N){
if (i%%50==0) cat(ch)
path.1[i,] <- path.1[i-1,] + sample(-D:D,2)
path.2[i,] <- path.2[i-1,] + sample(-D:D,2)
coef.1[i,] <- get.line(path.1[(i-1):i,])
coef.2[i,] <- get.line(path.2[(i-1):i,])
r.1 <- sqrt(max(rowSums((path.1[1:i,]-path.1[1,])^2)))
r.2 <- sqrt(max(rowSums((path.2[1:i,]-path.2[1,])^2)))
if (r.1+r.2 < d.start) next # paths do not overlap
ch <- "1"
d.1 <- sqrt(min(rowSums((path.2[1:i,]-path.1[1,])^2)))
d.2 <- sqrt(min(rowSums((path.1[1:i,]-path.2[1,])^2)))
if (d.1>r.1 & d.2>r.2) next
ch <- "2"
cross <- sapply(2:i,
function(k){seg.intersect(path.2[(k-1):k,],path.1[(i-1):i,],k)})
if (any(cross)) break
cross <- sapply(2:i,
function(k){seg.intersect(path.1[(k-1):k,],path.2[(i-1):i,],k)})
if (any(cross)) break
}
})
# 11111111112222222222222222222222
# user system elapsed
# 1016.82 0.13 1024.18
print(paste("End at Step: ",i))
# [1] "End at Step: 1624"
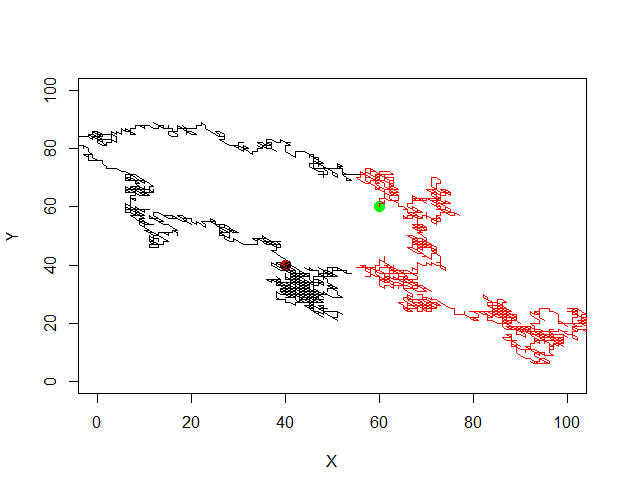
plot(0:100,0:100, type="n", xlab="X", ylab="Y")
points(path.1[1,1],path.1[1,2], pch=16, col="red", cex=1.5)
points(path.2[1,1],path.2[1,2], pch=16, col="green", cex=1.5)
lines(path.1[1:i,])
lines(path.2[1:i,],col="red")
Как указывает @CarlWitthoft, на каждом шаге вы должны проверять все предыдущие отрезки на наличие пересечений. Это создает серьезную проблему, потому что на каждом новом этапе i, имеются 2*(i-1) тесты для переездов. Итак, если вы доберетесь до перекрестка на шаге kбыло бы 2*k*(k+1) тесты. Если k ~O(10000)тогда могут быть потенциально 100-миллиметровые тесты.
Чтобы сделать это более эффективным, мы храним не только две новые точки на каждом шаге, но также наклон и пересечение вновь созданных отрезков. Это позволяет избежать пересчета наклона и перехвата для всех предыдущих отрезков на каждом шаге. Кроме того, мы рассчитываем радиус пути r для каждого пути на каждом шаге. Это расстояние между начальной точкой и точкой на пути, наиболее удаленном от начальной точки. Если расстояние между начальной точкой пути и ближайшей точкой на другом пути больше, чем радиус пути, пересечений быть не может, и мы можем пропустить сравнения отдельных сегментов для этого шага.
Ваша проблема интересна по другим причинам. Обычный способ проверки пересечений состоит в том, чтобы определить, находится ли пересечение между двумя линиями на каком-либо отрезке. Это громоздко, но просто. Однако есть много особых случаев: параллельны ли линии? Если так, они совпадают? Если так, то сегменты перекрываются? Как насчет вертикальных линий (наклон =Inf). Поскольку вы устанавливаете инкремент в случайное целое число на [-1,1], все эти возможности могут в конечном итоге произойти на пути с 10000 шагов. Так что функция seg.intersect(...) выше должен учитывать все эти возможности. Можно подумать, что в R есть функция, которая делает это, но я не смог ее найти, поэтому вот (грязная) версия:
get.line <- function(l) { # returns slope and intercept
if (diff(l)[1]==0) return(c(Inf,NA))
m <- diff(l)[2]/diff(l)[1]
b <- l[1,2]-m*l[1,1]
return(c(m,b))
}
is.between <- function(x,vec) { # test if x is between values in vec
return(x>=range(vec)[1] & x<=range(vec)[2])
}
special.cases = function(l1,l2, coeff) {
# points coincide: not a line segment!
if (rowSums(diff(l1)^2)==0 | rowSums(diff(l2)^2)==0) return(c(NA,FALSE))
# both lines vertical
if (is.infinite(coeff[1,1]) & is.infinite(coeff[2,1])) {
if (l1[1,1]!=l2[1,1]) return(c(NA,FALSE))
t1 <- is.between(l1[1,2],l2[,2]) | is.between(l1[2,2],l2[,2])
t2 <- is.between(l2[1,2],l1[,2]) | is.between(l2[2,2],l1[,2])
return(c(NA,t1|t2))
}
# only l1 is vertical
if (is.infinite(coeff[1,1]) & is.finite(coeff[2,1])) {
x <- l1[1,1]
y <- c(x,1) %*% coeff[2,]
return(c(x,y))
}
# only l2 is vertical
if (is.finite(coeff[1,1]) & is.infinite(coeff[2,1])) {
x <- l2[1,1]
y <- c(x,1) %*% coeff[1,]
return(c(x,y))
}
# parallel, non-coincident lines
if (diff(coeff[,1])==0 & diff(coeff[,2])!=0) return(c(NA,FALSE))
# parallel, coincident lines
if (diff(coeff[,1])==0 & diff(coeff[,2])==0) {
x <- l1[1,1]
y <- l1[1,2]
return(c(x,y))
}
# base case: finite slopes, not parallel
x <- -diff(coeff[,2])/diff(coeff[,1])
y <- c(x,1) %*% coeff[1,]
return(c(x,y))
}
seg.intersect <- function(l1,l2,i){
pts <- list(l1,l2)
coeff <- rbind(coef.1[i,],coef.2[i,])
z <- special.cases(l1,l2, coeff)
if (is.na(z[1])) return (z[2])
# print(coeff)
# print(z)
found <- do.call("&",
lapply(pts,function(x){is.between(z[1],x[,1]) & is.between(z[2],x[,2])}))
return(found)
}