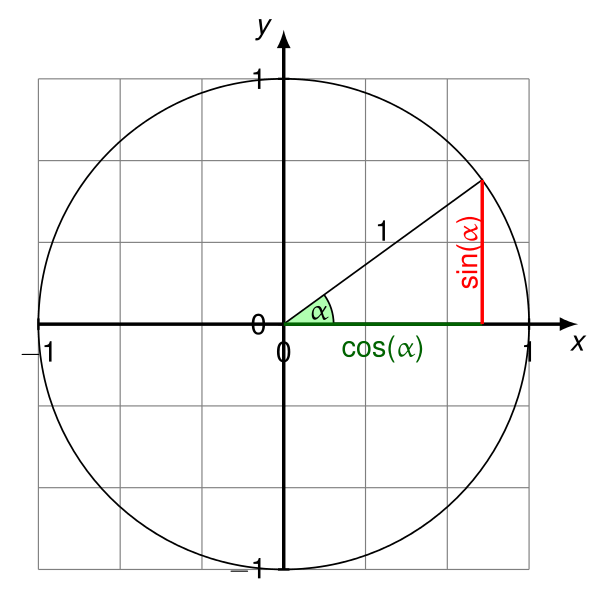
Как рассчитать угол между линией и горизонтальной осью?

В языке программирования (Python, C# и т. Д.) Мне нужно определить, как рассчитать угол между линией и горизонтальной осью?

Я думаю, что изображение лучше всего описывает то, что я хочу:

никакие слова не могут описать это

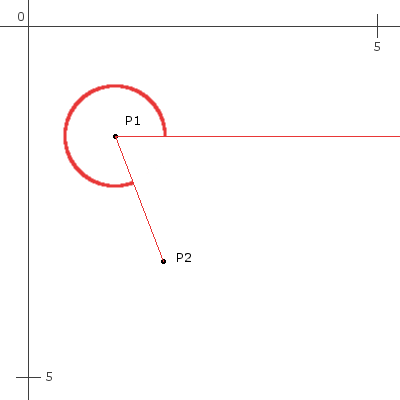
Учитывая (P1x, P1y) и (P2x, P2y), как лучше всего рассчитать этот угол? Источник находится в вершине, и используется только положительный квадрант.

Источник

8 ответов

Решение

Сначала найдите разницу между начальной и конечной точками (здесь это скорее направленный отрезок, а не "линия", поскольку линии простираются бесконечно и не начинаются в определенной точке).

deltaY = P2_y - P1_y
deltaX = P2_x - P1_x

Затем рассчитайте угол (который проходит от положительной оси X в P1 к положительной оси Y в P1).

angleInDegrees = arctan(deltaY / deltaX) * 180 / PI

Но arctan может не быть идеальным, потому что разделение различий таким образом сотрет различие, необходимое, чтобы различить, в каком квадранте находится угол (см. ниже). Используйте следующее вместо, если ваш язык включает в себя atan2 функция:

angleInDegrees = atan2(deltaY, deltaX) * 180 / PI

РЕДАКТИРОВАТЬ (22 февраля 2017 г.): В целом, однако, звонит atan2(deltaY,deltaX) просто чтобы получить правильный угол для cos а также sin может быть не элегантным. В этих случаях вы часто можете сделать следующее:

  1. Лечить (deltaX, deltaY) как вектор.
  2. Нормализуйте этот вектор в единичный вектор. Для этого делим deltaX а также deltaY по длине вектора (sqrt(deltaX*deltaX+deltaY*deltaY)), если длина не равна 0.
  3. После этого, deltaX теперь будет косинус угла между вектором и горизонтальной осью (в направлении от положительного X к положительной оси Y в P1).
  4. А также deltaY теперь будет синусом этого угла.
  5. Если длина вектора равна 0, у него не будет угла между ним и горизонтальной осью (поэтому у него не будет значимых синуса и косинуса).

РЕДАКТИРОВАТЬ (28 февраля 2017 г.): даже без нормализации (deltaX, deltaY):

  • Знак deltaX скажет вам, является ли косинус, описанный в шаге 3, положительным или отрицательным.
  • Знак deltaY скажет вам, является ли синус, описанный в шаге 4, положительным или отрицательным.
  • Признаки deltaX а также deltaY скажет вам, в каком квадранте находится угол, относительно положительной оси X в P1:
    • +deltaX, +deltaY: От 0 до 90 градусов.
    • -deltaX, +deltaY: От 90 до 180 градусов.
    • -deltaX, -deltaY: От 180 до 270 градусов (от -180 до -90 градусов).
    • +deltaX, -deltaY: От 270 до 360 градусов (от -90 до 0 градусов).

Реализация на Python с использованием радианов (предоставлена ​​19 июля 2015 г. Эриком Лещинским, который редактировал мой ответ):

from math import *
def angle_trunc(a):
    while a < 0.0:
        a += pi * 2
    return a

def getAngleBetweenPoints(x_orig, y_orig, x_landmark, y_landmark):
    deltaY = y_landmark - y_orig
    deltaX = x_landmark - x_orig
    return angle_trunc(atan2(deltaY, deltaX))

angle = getAngleBetweenPoints(5, 2, 1,4)
assert angle >= 0, "angle must be >= 0"
angle = getAngleBetweenPoints(1, 1, 2, 1)
assert angle == 0, "expecting angle to be 0"
angle = getAngleBetweenPoints(2, 1, 1, 1)
assert abs(pi - angle) <= 0.01, "expecting angle to be pi, it is: " + str(angle)
angle = getAngleBetweenPoints(2, 1, 2, 3)
assert abs(angle - pi/2) <= 0.01, "expecting angle to be pi/2, it is: " + str(angle)
angle = getAngleBetweenPoints(2, 1, 2, 0)
assert abs(angle - (pi+pi/2)) <= 0.01, "expecting angle to be pi+pi/2, it is: " + str(angle)
angle = getAngleBetweenPoints(1, 1, 2, 2)
assert abs(angle - (pi/4)) <= 0.01, "expecting angle to be pi/4, it is: " + str(angle)
angle = getAngleBetweenPoints(-1, -1, -2, -2)
assert abs(angle - (pi+pi/4)) <= 0.01, "expecting angle to be pi+pi/4, it is: " + str(angle)
angle = getAngleBetweenPoints(-1, -1, -1, 2)
assert abs(angle - (pi/2)) <= 0.01, "expecting angle to be pi/2, it is: " + str(angle)

Все тесты проходят. Смотрите https://en.wikipedia.org/wiki/Unit_circle

Источник

Извините, но я почти уверен, что ответ Питера неверен. Обратите внимание, что ось Y идет вниз по странице (обычно в графике). Таким образом, вычисление deltaY должно быть отменено, иначе вы получите неправильный ответ.

Рассматривать:

System.out.println (Math.toDegrees(Math.atan2(1,1)));
System.out.println (Math.toDegrees(Math.atan2(-1,1)));
System.out.println (Math.toDegrees(Math.atan2(1,-1)));
System.out.println (Math.toDegrees(Math.atan2(-1,-1)));

дает

45.0
-45.0
135.0
-135.0

Таким образом, если в приведенном выше примере P1 равен (1,1), а P2 равен (2,2) [потому что Y увеличивается вниз по странице], приведенный выше код даст 45,0 градуса для показанного примера, что неверно. Измените порядок расчета дельты, и он будет работать правильно.

Источник 
import math
from collections import namedtuple


Point = namedtuple("Point", ["x", "y"])


def get_angle(p1: Point, p2: Point) -> float:
    """Get the angle of this line with the horizontal axis."""
    dx = p2.x - p1.x
    dy = p2.y - p1.y
    theta = math.atan2(dy, dx)
    angle = math.degrees(theta)  # angle is in (-180, 180]
    if angle < 0:
        angle = 360 + angle
    return angle

Тестирование

Для проверки я позволяю гипотезе генерировать контрольные примеры.

import hypothesis.strategies as s
from hypothesis import given


@given(s.floats(min_value=0.0, max_value=360.0))
def test_angle(angle: float):
    epsilon = 0.0001
    x = math.cos(math.radians(angle))
    y = math.sin(math.radians(angle))
    p1 = Point(0, 0)
    p2 = Point(x, y)
    assert abs(get_angle(p1, p2) - angle) < epsilon
Источник

Я нашел решение в Python, которое работает хорошо!

from math import atan2,degrees

def GetAngleOfLineBetweenTwoPoints(p1, p2):
    return degrees(atan2(p2 - p1, 1))

print GetAngleOfLineBetweenTwoPoints(1,3)
Источник

На основании ссылки "Питер О".. Вот версия Java

private static final float angleBetweenPoints(PointF a, PointF b) {
float deltaY = b.y - a.y;
float deltaX = b.x - a.x;
return (float) (Math.atan2(deltaY, deltaX)); }
Источник

Рассматривая точный вопрос, помещая нас в "специальную" систему координат, где положительная ось означает перемещение ВНИЗ (например, экран или вид интерфейса), вам нужно адаптировать эту функцию следующим образом, а отрицательные координаты Y:

Пример в Swift 2.0

func angle_between_two_points(pa:CGPoint,pb:CGPoint)->Double{
    let deltaY:Double = (Double(-pb.y) - Double(-pa.y))
    let deltaX:Double = (Double(pb.x) - Double(pa.x))
    var a = atan2(deltaY,deltaX)
    while a < 0.0 {
        a = a + M_PI*2
    }
    return a
}

Эта функция дает правильный ответ на вопрос. Ответ в радианах, поэтому использование углов обзора в градусах:

let p1 = CGPoint(x: 1.5, y: 2) //estimated coords of p1 in question
let p2 = CGPoint(x: 2, y : 3) //estimated coords of p2 in question

print(angle_between_two_points(p1, pb: p2) / (M_PI/180))
//returns 296.56
Источник

Формула для угла от 0 до 2pi.

Существует х = х2-х1 и у = у2-у1. Формула работает для

любое значение х и у. Для x=y=0 результат не определен.

Р (х, у)= р ()- пи ()/2*(1 знак + (х))*(1-знак (у ^2))

     -pi()/4*(2+sign(x))*sign(y)

     -sign(x*y)*atan((abs(x)-abs(y))/(abs(x)+abs(y)))
Источник

Функция Matlab:

function [lineAngle] = getLineAngle(x1, y1, x2, y2) 
    deltaY = y2 - y1;
    deltaX = x2 - x1;

    lineAngle = rad2deg(atan2(deltaY, deltaX));

    if deltaY < 0
        lineAngle = lineAngle + 360;
    end
end
Источник 
deltaY = Math.Abs(P2.y - P1.y);
deltaX = Math.Abs(P2.x - P1.x);

angleInDegrees = Math.atan2(deltaY, deltaX) * 180 / PI

if(p2.y > p1.y) // Second point is lower than first, angle goes down (180-360)
{
  if(p2.x < p1.x)//Second point is to the left of first (180-270)
    angleInDegrees += 180;
  else (270-360)
    angleInDegrees += 270;
}
else if (p2.x < p1.x) //Second point is top left of first (90-180)
  angleInDegrees += 90;
Источник
Другие вопросы по тегам