Эффективный способ взять определитель n! хп! матрица в клене

Question

У меня большая матрица, п! хн!, за что мне нужно взять определитель. Для каждой перестановки n я ассоциирую

• вектор длиной 2n (это легко вычислить)
• полином от 2n переменных (произведение линейных факторов, вычисленных рекурсивно на n)

Матрица является оценочной матрицей для многочленов от векторов (представленных как точки). Таким образом, сигма-тау запись матрицы (индексированная перестановками) является полиномом для сигмы, вычисленной в векторе для тау.

Пример: для n=3если iполином (x1 - 4)(x3 - 5)(x4 - 4)(x6 - 1) и jТочка (2,2,1,3,5,2)тогда (i,j)ая запись матрицы будет (2 - 4)(1 - 5)(3 - 4)(2 - 1) = -8, Вот n=3так что точки в R^(3!) = R^6 и полиномы имеют 3!=6 переменные.

Моя цель - определить, является ли матрица неособой.

---

Мой подход сейчас таков:

• функция point берет перестановку и выводит вектор
• функция poly принимает перестановку и выводит полином
• функция nextPerm дает следующую перестановку в лексикографическом порядке

Сокращенная версия моего кода с псевдокодом такова:

B := [];
P := [];
w := [1,2,...,n];
while w <> NULL do
  B := B append poly(w);
  P := P append point(w);
  w := nextPerm(w);
od;

// BUILD A MATRIX IN MAPLE
M := Matrix(n!, (i,j) -> eval(B[i],P[j]));

// COMPUTE DETERMINANT IN MAPLE
det := LinearAlgebra[Determinant]( M );

// TELL ME IF IT'S NONSINGULAR
if det = 0 then return false;
else return true; fi;

Я работаю в Maple, используя встроенную функцию LinearAlgebra[Determinant], но все остальное - это встроенная функция, которая использует функции Maple низкого уровня (например, seq, convert а также cat).

Моя проблема в том, что это занимает слишком много времени, то есть я могу n=7 с терпением, но получать n=8 занимает дни. В идеале я хочу иметь возможность добраться до n=10,

У кого-нибудь есть идеи, как мне улучшить время? Я открыт для работы на другом языке, например, Matlab или C, но предпочел бы найти способ ускорить это в Maple.

Я понимаю, что это может быть трудно ответить без всех кровавых подробностей, но код для каждой функции, например point а также poly, уже оптимизирован, поэтому реальный вопрос здесь заключается в том, есть ли более быстрый способ получения определителя путем построения матрицы на лету или что-то в этом роде.

---

ОБНОВЛЕНИЕ: Вот две идеи, с которыми я играл, которые не работают:

1. Я могу хранить полиномы (так как они требуют времени для вычисления, я не хочу переделывать это, если смогу помочь) в вектор длины n!и вычислите точки на лету и вставьте эти значения в формулу перестановки для определителя: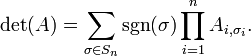

   

   Проблема в том, что это O(N!) в размере матрицы, так что для моего случая это будет O((n!)!), когда n=10, (n!)! = 3,628,800! который является способом большого, чтобы даже рассмотреть возможность.

2. Вычислить определитель, используя разложение LU. К счастью, главная диагональ моей матрицы отлична от нуля, так что это возможно. Так как это O(N^3) в размере матрицы, которая становится O((n!)^3) что гораздо ближе к выполнимым. Проблема, однако, заключается в том, что мне требуется хранить всю матрицу, что создает серьезную нагрузку на память, не говоря уже о времени выполнения. Так что это тоже не сработает, по крайней мере, без большей хитрости. Есть идеи?

Answer 1

Мне не ясно, является ли ваша проблема пространством или временем. Очевидно, что оба торгуют взад и вперед. Если вы хотите знать, является ли детерминант положительным или нет, то вам определенно следует LU разложение. Причина в том, что если A = LU с L нижняя треугольная и U верхний треугольный, затем

det(A) = det(L) det(U) = l_11 * ... * l_nn * u_11 * ... * u_nn

так что вам нужно только определить, если какой-либо из основных диагональных элементов L или же U является 0,

Чтобы упростить дальнейшее, используйте алгоритм Дулиттла, где l_ii = 1, Если в какой-то момент алгоритм выходит из строя, матрица является единственной, поэтому вы можете остановиться. Вот суть:

for k := 1, 2, ..., n do {
  for j := k, k+1, ..., n do {
    u_kj := a_kj - sum_{s=1...k-1} l_ks u_sj;
  }
  for i = k+1, k+2, ..., n do {
    l_ik := (a_ik - sum_{s=1...k-1} l_is u_sk)/u_kk;
  }
}

Ключ в том, что вы можете вычислить iй ряд U и iстолбец L в то же время, и вам нужно знать только предыдущую строку / столбец, чтобы двигаться вперед. Таким образом, вы параллельно обрабатываете столько, сколько можете, и сохраняете столько, сколько вам нужно. Так как вы можете вычислить записи a_ij по мере необходимости, для этого требуется хранить два вектора длины n генерируя еще два вектора длины n (ряды Uколонны L). Алгоритм занимает n^2 время. Возможно, вам удастся найти еще несколько хитростей, но это зависит от вашего компромисса между временем и пространством.

Answer 2

Не уверен, что следил за вашей проблемой; это (или сводится ли) к следующему?

У вас есть два вектора из n чисел, назовите их x а также cтогда матричный элемент является произведением k из (x_k+c_k)с каждой строкой / столбцом, соответствующим различным порядкам x а также c?

Если это так, то я считаю, что матрица будет единичной, когда есть повторяющиеся значения либо x или же c, поскольку матрица будет иметь повторяющиеся строки / столбцы. Попробуйте кучу Монте-Карло на меньшем n с различными значениями x а также c чтобы увидеть, является ли этот случай в общем случае не единичным - вполне вероятно, что это верно для 6, это будет верно для 10.

Что касается грубой силы, ваш метод:

1. Это не стартер
2. Будет работать намного быстрее (должно быть несколько секунд для n=7), хотя вместо LU вы, возможно, захотите попробовать SVD, который гораздо лучше даст вам понять, как хорошо себя ведет ваша матрица.