Как пройти через сеть подключенного узла подключенным способом?

Question

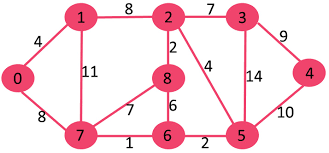
У меня есть структура данных, которую можно визуализировать как подключенную сеть, такую ​​как эта:

Я полагаю (без доказательств), что должна быть возможность пройти все узлы, всегда перемещаясь от одного узла к связанному узлу (возврат, конечно, необходим и разрешен - как вы бы сделали с древовидной структурой). Как это сделать?

Структура данных может быть записана в псевдокоде как:

node[N] nodes; // the network as an array of N nodes

class node {
  List<pt_to_node> friend_nodes;  // a list of pointers to connected nodes
}

Answer 1

Вы можете просто реализовать график со стеком для поиска в глубину или в очередь для поиска в ширину

например 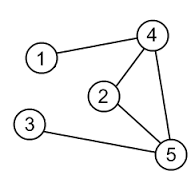Предположим, что мы собираемся начать с узла 1,

#include <vector>
#include <list>
#include <vector>
using namespace std;

class Graph
{
public:
    int vert; //number of vertices
    vector<list<int>> adj;

    Graph(int _v)
    {
        adj.resize(_v);
        vert = _v;
    }

    void addEdge(int v, int key)
    {
        adj[v].push_back(key);
        adj[key].push_back(v); // comment out if undirected
    }

    void bfs(int start);
    void dfs(int start);
};



void Graph::bfs(int start)
{

    vector<bool> visited(vert,false);

    list<int> queue;

    visited[start] = true; // visit the first node
    queue.push_back(start);


    while (!queue.empty())
    {
        start = queue.front();
        cout << start << " ";
        queue.pop_front();

        for (auto i = adj[start].begin(); i != adj[start].end(); ++i)
            if (!visited[*i])
            {
                visited[*i] = true;
                queue.push_back(*i);
            }
    }
    cout << endl;
}

void Graph::dfs(int start)
{
    vector<bool> visited(vert,false);

    vector<int> stack;

    visited[start] = true;
    stack.push_back(start);

    while (!stack.empty())
    {
        start = stack.back();
        cout << start << " ";
        stack.pop_back();

        for (auto i = adj[start].begin(); i != adj[start].end(); ++i)
            if (!visited[*i])
            {
                visited[*i] = true;
                stack.push_back(*i);
            }
    }
    cout << endl;
}

int main()
{

    Graph g(6); // number of vertices we need
    g.addEdge(1, 4);
    g.addEdge(4, 2);
    g.addEdge(4, 5);
    g.addEdge(2, 5);
    g.addEdge(5, 3);

    g.bfs(1); // start with 1
    g.dfs(1);


}

Результатами являются DFS: 1 4 2 5 3 и BFS 1 4 5 3 2. Однако в реальной сети каждое ребро имеет значение веса, которое означает расстояние или скорость ребра.