Среднее квадратное смещение

Question

Я исследую движение частицы размером один микрометр в плазме низкой плотности. С помощью так называемого дальнего микроскопа я записал движение частицы (2726 изображений, fps=60 Гц).

Данные x,y в мм доступны здесь: http://pastebin.com/qdMsaUHD

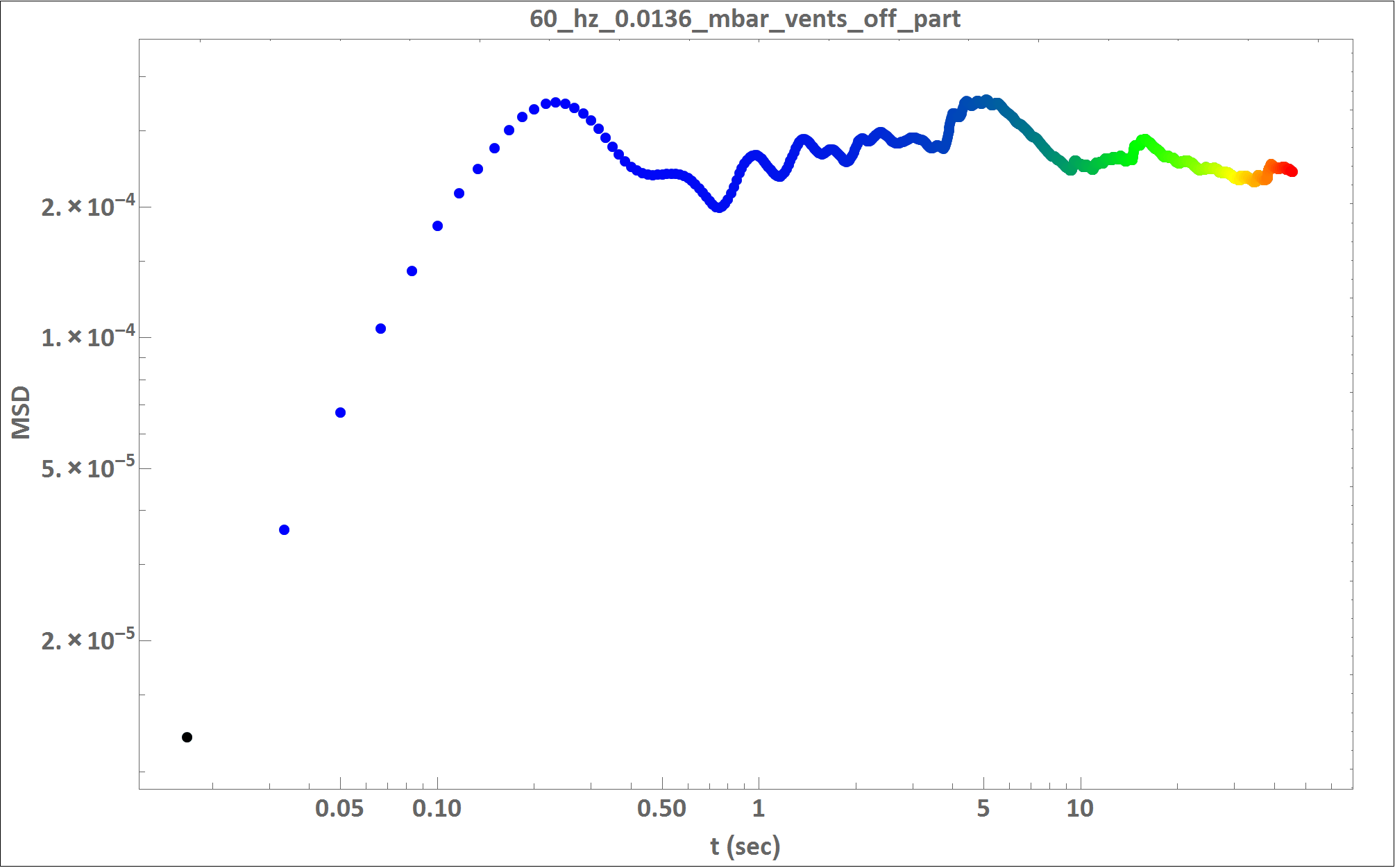
С Mathematica я получил следующий логарифмический график для среднего квадрата смещения (MSD):

Я новичок в Python и искал примеры того, как читать в 2D координаты из файла, вычислять и отображать MSD (среднее и стандартное отклонение).

Я видел, что есть некоторые ответы, которые показывают, как рассчитать MSD, но я не могу адаптировать их к своим данным.

Я был бы очень признателен, если бы кто-нибудь смог показать мне полный исходный код Python (со всем импортом), который необходим для решения моей проблемы.

Для меня это будет отличная возможность и очень конкретная проблема - начать программирование на Python. Заранее большое спасибо за вашу помощь.

Я попробовал следующее из одного из ответов ( Вычисление среднеквадратичного смещения 2-го случайного блуждания в Python), но код выдал ошибки.

import numpy as np
import matplotlib.pyplot as plt

data= [[49.136926889715, 48.4423791821561],
[48.8104534783146, 51.0491783022365],
[48.5231487166892, 53.3485202014],
[48.2320069851565, 55.2569539728078],
[47.8817794028032, 56.993296770262],
[47.381875792142, 58.179721166033],
...
[45.3409434914228, 49.0259838546922]]

def compute_MSD(path):
   totalsize=len(path)
   msd=[]
   for i in range(totalsize-1):
       j=i+1
       msd.append(np.sum((path[0:-j]-path[j::])**2)/float(totalsize-j))

   msd=np.array(msd)
   return msd

result=compute_MSD(data)

plt.plot(result)
plt.show()

Answer 1

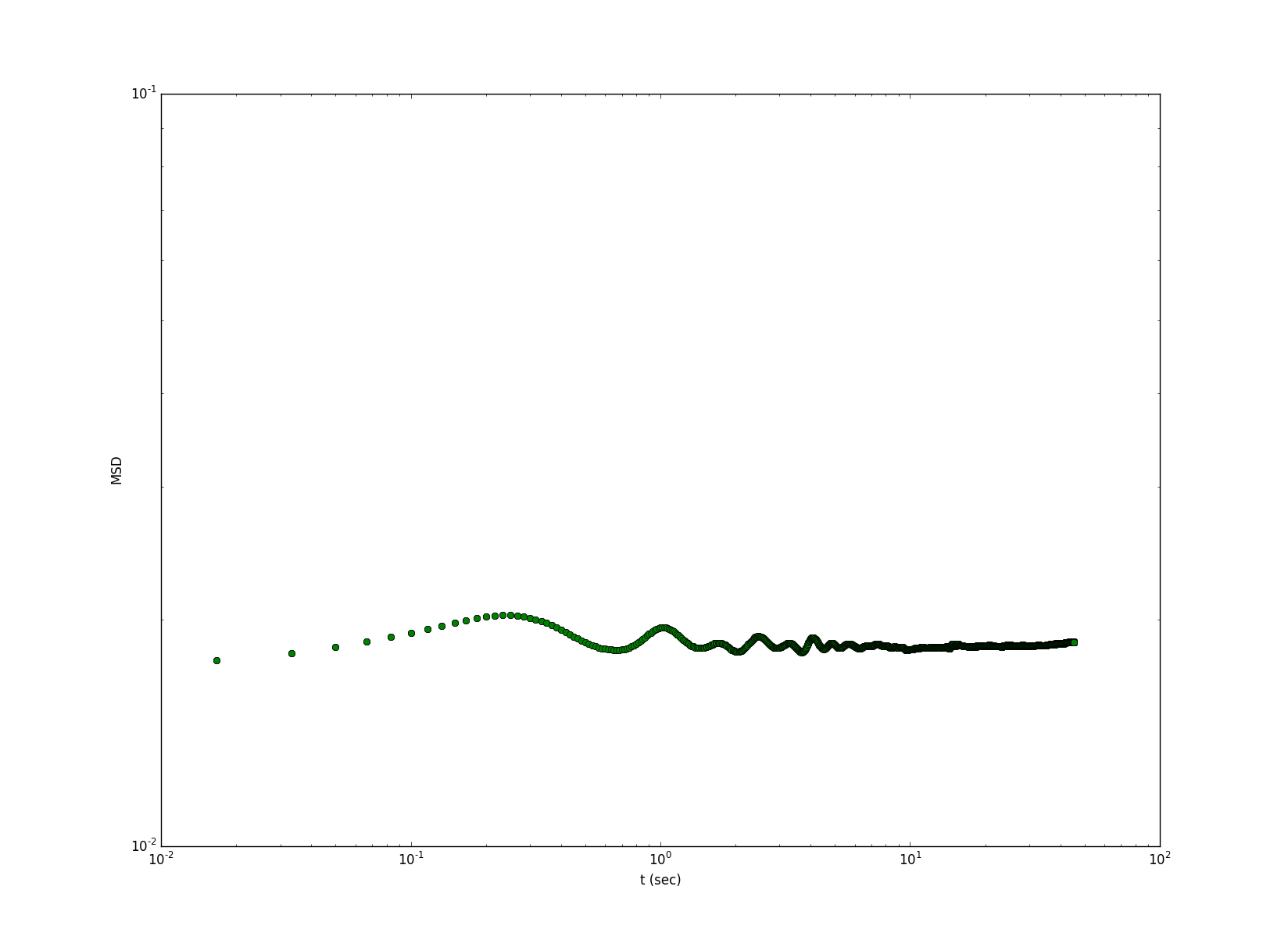
Мои графики выглядят немного иначе, чем ваши, что, вероятно, связано с неправильным пониманием того, что именно вы рассчитываете, однако я считаю, что это относится к основной идее.

plasma = [[0.09296720430107527, 0.09280376344086022],
[0.09230113636363636, 0.09769886363636364],
[0.09130555555555556, 0.10198777777777777],
...

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt

df = pd.DataFrame(plasma, columns=['x', 'y'])
df['time'] = np.arange(0,len(df)) / 60.0
df['dist'] = np.sqrt(df['x']**2 + df['y']**2)
df['MSD'] = pd.rolling_mean((np.abs(df['dist'])**2), len(df), min_periods=1)

Выше мое толкование того, что вы подразумеваете под MSD. Я использую расстояние от начала координат, т.е. sqrt(x^2 + y^2) а затем применяя следующее определение

Затем вы можете создать сюжет с помощью http://matplotlib.org/ следующим образом

plt.loglog(df['time'], df['MSD'], 'o')
plt.xlabel('t (sec)')
plt.ylabel('MSD')
plt.show()

Если вы хотите подправить / уточнить графики, отличное место, чтобы разобраться с matplotlib - здесь раздел учебника.

Answer 2

Numpy имеет стандартную функцию для расчета стандартного отклонения. Ты можешь использовать numpy.std функция. Дайте список в качестве входных данных, и он будет выводить результат. Вам не нужно писать эти циклы, чтобы сделать это.

Чтобы получить тот же результат, что и набор MATLAB ddof = 1 в аргументе numpy.std функция.

Обратитесь сюда за примерами.