OpenCV warpperspective

Question

По какой-то причине всякий раз, когда я использую функцию warcPerspective() OpenCV, окончательное деформированное изображение не содержит всего исходного изображения. Кажется, левая часть изображения обрезана. Я думаю, что причина этого заключается в том, что деформированное изображение создается в крайнем левом положении холста для функции warpPerspective(). Есть ли способ исправить это? Спасибо

Answer 1

Проблема возникает из-за того, что гомография отображает часть изображения на отрицательные значения x,y, которые находятся за пределами области изображения и поэтому не могут быть нанесены на график. то, что мы хотим сделать, это сместить деформированный вывод на некоторое количество пикселей, чтобы "шунтировать" все деформированное изображение в положительные координаты (и, следовательно, внутри области изображения).

Гомографии могут быть объединены с использованием умножения матриц (именно поэтому они такие мощные). Если A и B являются гомографиями, то AB представляет гомографию, которая сначала применяет B, а затем A.

Из-за этого все, что нам нужно сделать, чтобы сместить вывод, это создать матрицу гомографии для перевода на некоторое смещение, а затем предварительно умножить ее на нашу исходную матрицу гомографии.

Двухмерная матрица гомографии выглядит так:

[R11,R12,T1]
[R21,R22,T2]
[ P , P , 1]

где R представляет матрицу вращения, T представляет перевод, и P представляет перспективную деформацию. Итак, чисто поступательная гомография выглядит так:

[ 1 , 0 , x_offset]
[ 0 , 1 , y_offset]
[ 0 , 0 ,    1    ]

Так что просто умножьте вашу гомографию на матрицу, аналогичную приведенной выше, и ваше выходное изображение будет смещено.

(Убедитесь, что вы используете умножение матриц, а не умножение элементов!)

Answer 2

Ответ Мэтта - хорошее начало, и он прав, говоря, что вам нужно умножить свою гомографию на

[ 1 , 0 , x_offset]
[ 0 , 1 , y_offset]
[ 0 , 0 ,    1    ]

Но он не указывает, что такое x_offset и y_offset. В других ответах говорилось, что просто используйте перспективное преобразование, но это неверно. Вы хотите использовать ОБРАТНОЕ перспективное преобразование.

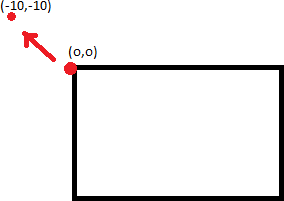
То, что точка 0,0 преобразуется, скажем, в -10,-10, не означает, что смещение изображения на 10,10 приведет к не обрезанному изображению. Это потому, что точка 10,10 не обязательно отображается в 0,0.
Что вы хотите сделать, так это выяснить, какая точка будет отображаться в 0,0, и сдвинуть изображение на столько. Для этого вы берете инверсию (cv2.invert) гомографии и применяете перспективу Transform.

не подразумевает:

Вам нужно применить обратное преобразование, чтобы найти правильные точки.

Это даст правильные значения x_offset и y_offset для выравнивания левой верхней точки. Оттуда, чтобы найти правильную ограничивающую рамку и идеально вписать все изображение, вам необходимо выяснить перекос (насколько изображение наклонено влево или вверх после вашего обычного, необратного преобразования) и добавить эту величину к вашим x_offset и y_offset также.

РЕДАКТИРОВАТЬ: это все теория. В моих тестах изображения на несколько пикселей отличаются, я не уверен, почему.

Answer 3

Секрет состоит из двух частей: матрица преобразования (гомография) и размер получаемого изображения.

• вычислить правильное преобразование с помощью getPerspectiveTransform(). Возьмите 4 точки из исходного изображения, вычислите их правильное положение в пункте назначения, поместите их в два вектора в одном и том же порядке и используйте их для вычисления матрицы перспективного преобразования.

• Убедитесь, что размер целевого изображения (третий параметр для warpPerspective()) - это именно то, что вам нужно. Определите его как размер (myWidth, myHeight).

Answer 4

Я сделал один метод... Он работает.

  perspectiveTransform(obj_corners,scene_corners,H);
int maxCols(0),maxRows(0);

 for(int i=0;i<scene_corners.size();i++)
{
   if(maxRows < scene_corners.at(i).y)
        maxRows = scene_corners.at(i).y;
   if(maxCols < scene_corners.at(i).x)
        maxCols = scene_corners.at(i).x;
}

Я просто нахожу максимум из х точек и у точек соответственно и положить его на

warpPerspective( tmp, transformedImage, homography, Size( maxCols, maxRows ) );

Answer 5

Попробуйте ниже homography_warp,

void homography_warp(const cv::Mat& src, const cv::Mat& H, cv::Mat& dst);

src это исходное изображение.

H это твоя гомография

dst это искаженное изображение.

homography_warp измените свою гомографию, как описано Matt Freeman в его ответе /questions/45852477/opencv-warpperspective/45852562#45852562

// Convert a vector of non-homogeneous 2D points to a vector of homogenehous 2D points.
void to_homogeneous(const std::vector< cv::Point2f >& non_homogeneous, std::vector< cv::Point3f >& homogeneous)
{
    homogeneous.resize(non_homogeneous.size());
    for (size_t i = 0; i < non_homogeneous.size(); i++) {
        homogeneous[i].x = non_homogeneous[i].x;
        homogeneous[i].y = non_homogeneous[i].y;
        homogeneous[i].z = 1.0;
    }
}

// Convert a vector of homogeneous 2D points to a vector of non-homogenehous 2D points.
void from_homogeneous(const std::vector< cv::Point3f >& homogeneous, std::vector< cv::Point2f >& non_homogeneous)
{
    non_homogeneous.resize(homogeneous.size());
    for (size_t i = 0; i < non_homogeneous.size(); i++) {
        non_homogeneous[i].x = homogeneous[i].x / homogeneous[i].z;
        non_homogeneous[i].y = homogeneous[i].y / homogeneous[i].z;
    }
}

// Transform a vector of 2D non-homogeneous points via an homography.
std::vector<cv::Point2f> transform_via_homography(const std::vector<cv::Point2f>& points, const cv::Matx33f& homography)
{
    std::vector<cv::Point3f> ph;
    to_homogeneous(points, ph);
    for (size_t i = 0; i < ph.size(); i++) {
        ph[i] = homography*ph[i];
    }
    std::vector<cv::Point2f> r;
    from_homogeneous(ph, r);
    return r;
}

// Find the bounding box of a vector of 2D non-homogeneous points.
cv::Rect_<float> bounding_box(const std::vector<cv::Point2f>& p)
{
    cv::Rect_<float> r;
    float x_min = std::min_element(p.begin(), p.end(), [](const cv::Point2f& lhs, const cv::Point2f& rhs) {return lhs.x < rhs.x; })->x;
    float x_max = std::max_element(p.begin(), p.end(), [](const cv::Point2f& lhs, const cv::Point2f& rhs) {return lhs.x < rhs.x; })->x;
    float y_min = std::min_element(p.begin(), p.end(), [](const cv::Point2f& lhs, const cv::Point2f& rhs) {return lhs.y < rhs.y; })->y;
    float y_max = std::max_element(p.begin(), p.end(), [](const cv::Point2f& lhs, const cv::Point2f& rhs) {return lhs.y < rhs.y; })->y;
    return cv::Rect_<float>(x_min, y_min, x_max - x_min, y_max - y_min);
}

// Warp the image src into the image dst through the homography H.
// The resulting dst image contains the entire warped image, this
// behaviour is the same of Octave's imperspectivewarp (in the 'image'
// package) behaviour when the argument bbox is equal to 'loose'.
// See http://octave.sourceforge.net/image/function/imperspectivewarp.html
void homography_warp(const cv::Mat& src, const cv::Mat& H, cv::Mat& dst)
{
    std::vector< cv::Point2f > corners;
    corners.push_back(cv::Point2f(0, 0));
    corners.push_back(cv::Point2f(src.cols, 0));
    corners.push_back(cv::Point2f(0, src.rows));
    corners.push_back(cv::Point2f(src.cols, src.rows));

    std::vector< cv::Point2f > projected = transform_via_homography(corners, H);
    cv::Rect_<float> bb = bounding_box(projected);

    cv::Mat_<double> translation = (cv::Mat_<double>(3, 3) << 1, 0, -bb.tl().x, 0, 1, -bb.tl().y, 0, 0, 1);

    cv::warpPerspective(src, dst, translation*H, bb.size());
}

Answer 6

Простой способ решить проблему проецирования деформированного изображения за пределы вывода деформирования - это перевести деформированное изображение в правильное положение. Основная проблема заключается в поиске правильного смещения для перевода.

Концепция перевода уже обсуждается в других приведенных здесь ответах, поэтому я объясню, как получить правильное смещение. Идея состоит в том, что совпадающие элементы на двух изображениях должны иметь одинаковые координаты в конечном сшитом изображении.

Допустим, мы называем изображения следующим образом:

• 'исходное изображение' (si): изображение, которое нужно исказить
• 'конечное изображение' (di): изображение, перспектива которого будет искажена "исходным изображением"
• 'искаженное исходное изображение' (wsi): исходное изображение после его деформации в перспективу целевого изображения

Вот что вам нужно сделать, чтобы рассчитать смещение для перевода:

1. После того, как вы выбрали подходящие совпадения и нашли маску из гомографии, сохраните ключевую точку наилучшего совпадения (точка с минимальным расстоянием и являющаяся второстепенной (должна получить значение 1 в маске, полученной из расчета гомографии)) в si а также di. Скажем, ключевой момент лучшего матча вsi and диisbm_siandbm_di` соответственно.

   bm_si = [x1, y1,1]

   bm_di = [x2, y2, 1]

2. Найдите положение bm_si в wsi просто умножив его на матрицу гомографии (H).bm_wsi = np.dot(H,bm_si)

   bm_wsi = [x/bm_wsi[2] for x in bm_wsi]

3. В зависимости от того, где вы будете размещать di на выходе si коробление (=wsi), настроить bm_di

   Скажем, если вы переключаетесь с левого изображения на правое (например, левое изображение si и правильное изображение di) тогда вы разместите di на правой стороне wsi и, следовательно bm_di[0] += si.shape[0]

4. Теперь после описанных выше шагов

   x_offset = bm_di[0] - bm_si[0]

   y_offset = bm_di[1] - bm_si[1]

5. Используя вычисленное смещение, найдите новую матрицу гомографии и деформируйте si.

   T = np.array([[1, 0, x_offset], [0, 1, y_offset], [0, 0, 1]])

   translated_H = np.dot(T.H)

   wsi_frame_size = tuple(2*x for x in si.shape)

   stitched = cv2.warpPerspective(si, translated_H, wsi_frame_size)

   stitched[0:si.shape[0],si.shape[1]:] = di

Answer 7

warpPerspective() работает нормально. Не нужно его переписывать. Вы, вероятно, используете это неправильно.

Помните следующие советы:

1. (0,0) пикселей не в центре, а в левом верхнем углу. Таким образом, если вы увеличите изображение х2, вы потеряете нижнюю и правую части, а не границу (как в Matlab).
2. Если вы деформируете изображение дважды, лучше умножить преобразования и активировать функцию один раз.
3. Я думаю, что это работает только на матрицах char / int, а не на float / double.
4. Когда у вас есть преобразование, сначала применяются масштабирование / наклон / поворот / перспектива и, наконец, перевод. Поэтому, если часть изображения отсутствует, просто измените переход (две верхние строки последнего столбца) в матрице.

Answer 8

Возможно, это мертвая тема, но я столкнулся с аналогичной проблемой. Я пытался сделать AR, перекрывая два кадра. Моя прямая трансляция с камеры (кадр 1) была меньше изображения, которое я пытался на нее проецировать. Итак, я уменьшил размеры целевого изображения, чтобы оно соответствовало живому видео. После этого cv::warpPerspective выдал правильный результат. Искаженное изображение находилось в пределах кадра живого видео.

Размер окна: 600*337.

Размер исходного изображения: 720*900.

Измените размер изображения (это входные данные для cv::warpPerspective) до: 600*377, и оно должно работать.

Искаженное изображение слишком велико и не помещается в рамку (без изменения размера)

Исправить искаженное изображение после изменения размера

Answer 9

Координаты изображения начинаются и вращаются вокруг точки 0,0, которая является верхним левым углом изображения (четвертый квадрант в двумерной декартовой системе). После поворота изображения по часовой стрелке (перемещение изображения в третий квадрант) сдвиг вправо (положительный сдвиг оси X со значением: положительная исходная высота изображения) вернет изображение обратно в «кадр».

      height = 220
scaleX, shearX   = 0.0, -1.0
shearY, scaleY   = 1.0, 0.0
transX, transY   = height, 0
shearXZ, shearYZ = 0.0, 0.0

warpMatrix = np.array([[scaleX, shearX, transX],
                      [shearY, scaleY, transY],
                      [shearXZ, shearYZ, 1]])
print(warpMatrix)

выходы:

      [[  0.  -1. 220.]
 [  1.   0.   0.]
 [  0.   0.   1.]]

А потом:

      rotatedImg = cv2.warpPerspective(src         = img,
                                 M           = warpMatrix,
                                 dsize       = (height, width),
                                 flags       = cv2.INTER_LINEAR,
                                 borderMode  = cv2.BORDER_CONSTANT,
                                 borderValue = 0)

Answer 10

Это мое решение

поскольку третий параметр в "warpPerspective()" является матрицей преобразования,

мы можем создать матрицу преобразования, которая сначала перемещает изображение назад, затем поворачивает изображение и, наконец, перемещает изображение вперед.

В моем случае у меня есть изображение с высотой 160 пикселей и шириной 160 пикселей. Я хочу повернуть изображение вокруг [80,80] вместо [0,0]

во-первых, перемещает изображение назад (это означает, что T1)

затем поворачивает изображение (что означает R)

наконец, перемещает изображение вперед (что означает T2)

void rotateImage(Mat &src_img,int degree)
{
float radian=(degree/180.0)*M_PI;
Mat R(3,3,CV_32FC1,Scalar(0));
R.at<float>(0,0)=cos(radian);R.at<float>(0,1)=-sin(radian);
R.at<float>(1,0)=sin(radian);R.at<float>(1,1)=cos(radian);
R.at<float>(2,2)=1;
Mat T1(3,3,CV_32FC1,Scalar(0));
T1.at<float>(0,2)=-80;
T1.at<float>(1,2)=-80;
T1.at<float>(0,0)=1;
T1.at<float>(1,1)=1;
T1.at<float>(2,2)=1;
Mat T2(3,3,CV_32FC1,Scalar(0));
T2.at<float>(0,2)=80;
T2.at<float>(1,2)=80;
T2.at<float>(0,0)=1;
T2.at<float>(1,1)=1;
T2.at<float>(2,2)=1;

std::cerr<<T1<<std::endl;
std::cerr<<R<<std::endl;
std::cerr<<T2<<std::endl;
std::cerr<<T2*R*T1<<"\n"<<std::endl;

cv::warpPerspective(src_img, src_img, T2*R*T1, src_img.size(), cv::INTER_LINEAR);
}

Answer 11

Вот решение opencv-python для вашей проблемы, я поместил его на github: https://github.com/Sanster/notes/blob/master/opencv/warpPerspective.md

Ключевой момент, как сказал пользователь user3094631, получить две матрицы перевода (T1, T2) и применить к матрице поворота (M) T2*M*T1

В коде, который я даю, T1 от центральной точки исходного изображения, а T2 от левой верхней точки преобразованного ограничивающего прямоугольника. Преобразованный boundingBox исходит из исходных угловых точек:

height = img.shape[0]
width = img.shape[1]
#..get T1
#..get M
pnts = np.asarray([
    [0, 0],
    [width, 0],
    [width, height],
    [0, height]
    ], dtype=np.float32)
pnts = np.array([pnts])
dst_pnts = cv2.perspectiveTransform(pnts, M * T1)[0]
dst_pnts = np.asarray(dst_pnts, dtype=np.float32)
bbox = cv2.boundingRect(dst_pnts)
T2 = np.matrix([[1., 0., 0 - bbox[0]],
                [0., 1., 0 - bbox[1]],
                [0., 0., 1.]])