Подгонка нескольких гауссианов к данным в питоне

Question

Мне просто интересно, есть ли простой способ реализовать гауссово / лоренцево подгонку к 10 пикам и извлечь fwhm, а также определить положение fwhm по значениям x. Сложный способ состоит в том, чтобы отделить пики и подогнать данные и извлечь fwhm.

Данные [ https://drive.google.com/file/d/0B6sUnnbyNGuOT2RZb2UwYXU4dlE/view?usp=sharing].

Любой совет с благодарностью. Благодарю.

from scipy.optimize import curve_fit
import numpy as np
import matplotlib.pyplot as plt

data = np.loadtxt('data.txt', delimiter=',')
x, y = data

plt.plot(x,y)
plt.show()

def func(x, *params):
    y = np.zeros_like(x)
    print len(params)
    for i in range(0, len(params), 3):
        ctr = params[i]
        amp = params[i+1]
        wid = params[i+2]
        y = y + amp * np.exp( -((x - ctr)/wid)**2)



guess = [0, 60000, 80, 1000, 60000, 80]
for i in range(12):
    guess += [60+80*i, 46000, 25]


popt, pcov = curve_fit(func, x, y, p0=guess)
print popt
fit = func(x, *popt)

plt.plot(x, y)
plt.plot(x, fit , 'r-')
plt.show()



Traceback (most recent call last):
File "C:\Users\test.py", line 33, in <module>
popt, pcov = curve_fit(func, x, y, p0=guess)
File "C:\Python27\lib\site-packages\scipy\optimize\minpack.py", line 533, in curve_fit
res = leastsq(func, p0, args=args, full_output=1, **kw)
File "C:\Python27\lib\site-packages\scipy\optimize\minpack.py", line 368, in leastsq
shape, dtype = _check_func('leastsq', 'func', func, x0, args, n)
File "C:\Python27\lib\site-packages\scipy\optimize\minpack.py", line 19, in _check_func
res = atleast_1d(thefunc(*((x0[:numinputs],) + args)))
File "C:\Python27\lib\site-packages\scipy\optimize\minpack.py", line 444, in    _ general_function
return function(xdata, *params) - ydata
TypeError: unsupported operand type(s) for -: 'NoneType' and 'float'

Answer 1

Это требует нелинейной подгонки. Хороший инструмент для этого - Scipy's curve_fit функция.

Использовать curve_fitнам нужна модельная функция, назовите ее func, что занимает x и наши (угаданные) параметры в качестве аргументов и возвращает соответствующие значения для y, В качестве нашей модели мы используем сумму гауссиан:

from scipy.optimize import curve_fit
import numpy as np

def func(x, *params):
    y = np.zeros_like(x)
    for i in range(0, len(params), 3):
        ctr = params[i]
        amp = params[i+1]
        wid = params[i+2]
        y = y + amp * np.exp( -((x - ctr)/wid)**2)
    return y

Теперь давайте создадим первоначальное предположение для наших параметров. Это предположение начинается с пиков в x=0 а также x=1,000 с амплитудой 60000 и шириной электронного сгиба 80. Затем мы добавляем возможные пики в x=60, 140, 220, ... с амплитудой 46000 и шириной 25:

guess = [0, 60000, 80, 1000, 60000, 80]
for i in range(12):
    guess += [60+80*i, 46000, 25]

Теперь мы готовы выполнить посадку:

popt, pcov = curve_fit(func, x, y, p0=guess)
fit = func(x, *popt)

Чтобы увидеть, насколько хорошо мы это сделали, давайте построим y значения (сплошная черная кривая) и fit (пунктирная красная кривая) против x:

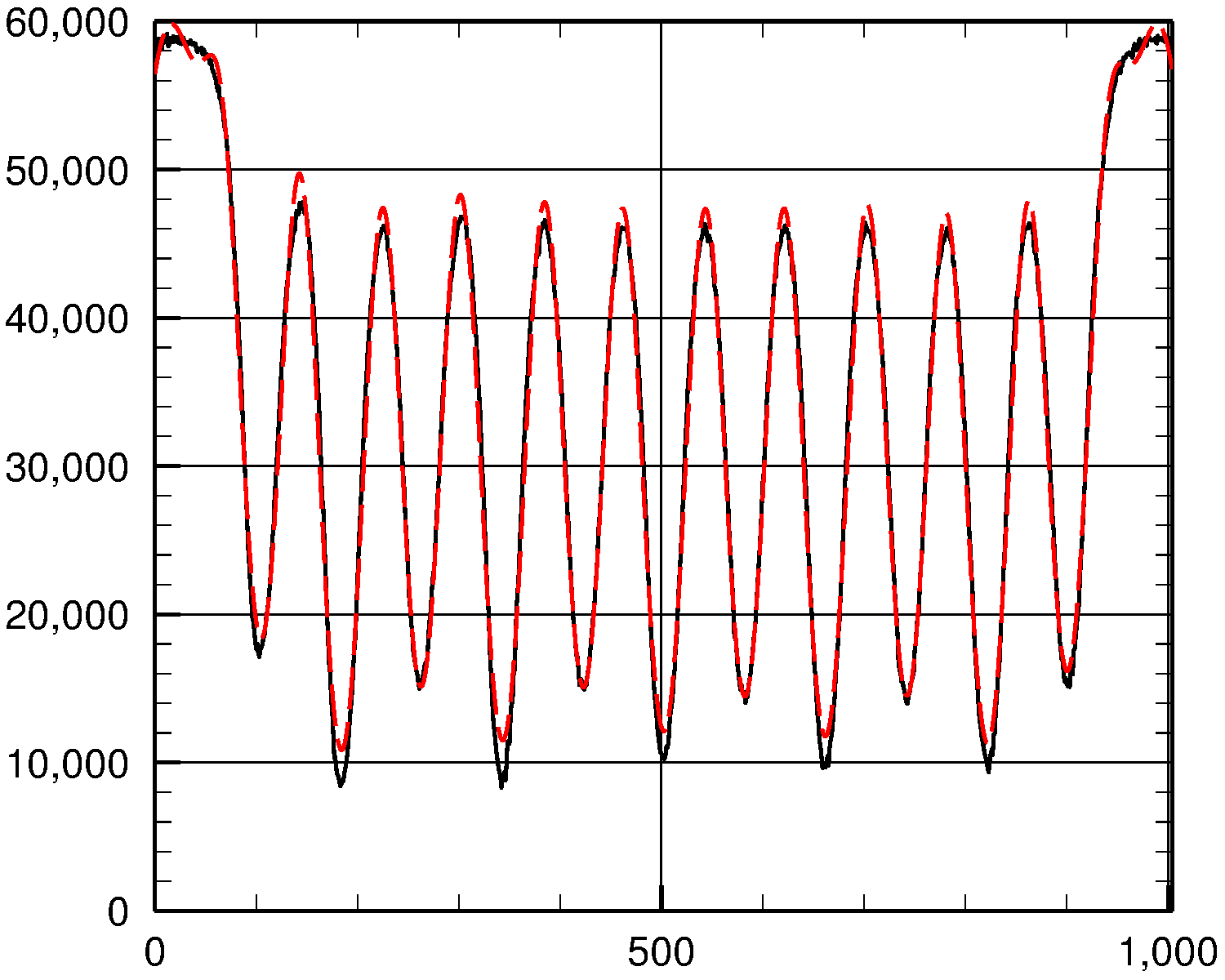
Как видите, подгонка довольно хорошая.

Полный рабочий код

from scipy.optimize import curve_fit
import numpy as np
import matplotlib.pyplot as plt

data = np.loadtxt('data.txt', delimiter=',')
x, y = data

plt.plot(x,y)
plt.show()

def func(x, *params):
    y = np.zeros_like(x)
    for i in range(0, len(params), 3):
        ctr = params[i]
        amp = params[i+1]
        wid = params[i+2]
        y = y + amp * np.exp( -((x - ctr)/wid)**2)
    return y

guess = [0, 60000, 80, 1000, 60000, 80]
for i in range(12):
    guess += [60+80*i, 46000, 25]   

popt, pcov = curve_fit(func, x, y, p0=guess)
print popt
fit = func(x, *popt)

plt.plot(x, y)
plt.plot(x, fit , 'r-')
plt.show()

Answer 2

Ответ @john1024 хорош, но требует ручного процесса для создания первоначального предположения. вот простой способ автоматизировать начальное предположение. замените соответствующие 3 строки кода john1024 следующим:

    import scipy.signal
    i_pk = scipy.signal.find_peaks_cwt(y, widths=range(3,len(x)//Npks))
    DX = (np.max(x)-np.min(x))/float(Npks) # starting guess for component width
    guess = np.ravel([[x[i], y[i], DX] for i in i_pk]) # starting guess for (x, amp, width) for each component

Answer 3

ИМХО, в таких задачах, как эта, всегда целесообразно отображать остаток (данные - модель). Вы также захотите взглянуть на ChiSq подгонки.