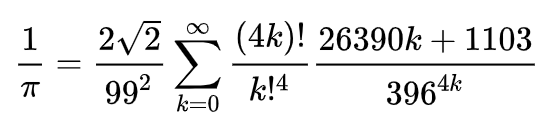В Julia 1.0+ выведите первые 2000 цифр числа после десятичной точки
В учебных целях, как бы вы написали "юлианский" код Julia 1.0+ для печати первых 2000 цифр pi после десятичной точки? Результат, в Julia REPL, должен совпадать с этим пи сайта.
Ожидаемый результат:
julia> include("solution.jl")
Pi to 2,000 digits to right of decimal point is:
3.
14159265358979323846264338327950288419716939937510
58209749445923078164062862089986280348253421170679
82148086513282306647093844609550582231725359408128
48111745028410270193852110555964462294895493038196
44288109756659334461284756482337867831652712019091
45648566923460348610454326648213393607260249141273
72458700660631558817488152092096282925409171536436
78925903600113305305488204665213841469519415116094
33057270365759591953092186117381932611793105118548
07446237996274956735188575272489122793818301194912
98336733624406566430860213949463952247371907021798
60943702770539217176293176752384674818467669405132
00056812714526356082778577134275778960917363717872
14684409012249534301465495853710507922796892589235
42019956112129021960864034418159813629774771309960
51870721134999999837297804995105973173281609631859
50244594553469083026425223082533446850352619311881
71010003137838752886587533208381420617177669147303
59825349042875546873115956286388235378759375195778
18577805321712268066130019278766111959092164201989
38095257201065485863278865936153381827968230301952
03530185296899577362259941389124972177528347913151
55748572424541506959508295331168617278558890750983
81754637464939319255060400927701671139009848824012
85836160356370766010471018194295559619894676783744
94482553797747268471040475346462080466842590694912
93313677028989152104752162056966024058038150193511
25338243003558764024749647326391419927260426992279
67823547816360093417216412199245863150302861829745
55706749838505494588586926995690927210797509302955
32116534498720275596023648066549911988183479775356
63698074265425278625518184175746728909777727938000
81647060016145249192173217214772350141441973568548
16136115735255213347574184946843852332390739414333
45477624168625189835694855620992192221842725502542
56887671790494601653466804988627232791786085784383
82796797668145410095388378636095068006422512520511
73929848960841284886269456042419652850222106611863
06744278622039194945047123713786960956364371917287
46776465757396241389086583264599581339047802759009
3 ответа
Удивительный ключ к решению этого вопроса с очень небольшим кодом для относительного новичка Джулии, как я и, возможно, кто-то еще, заключается в том, что pi Константа в Юлии не жестко запрограммирована на некоторое количество цифр, как во многих других языках. У Юлии pi константа "меняет" свою точность, основываясь на базовой точности текущей операции, например, текущей Джулии BigFloat Точность в этом примере.
Так что, если мы установим BigFloat точность до 2,001 десятичных знаков и сделать BigFloat результат операции с piМы должны получить желаемый ответ.
Самый простой способ сделать эту операцию, о которой я знаю, это просто изменить pi к BigFloat тип. Это приведет к типу результата BigFloat, как показано этим кодом.
julia> VERSION
v"1.1.0"
julia> typeof(BigFloat(pi)) # big"1" * pi also works
BigFloat
Исходный вопрос может быть решен с помощью этого метода, как показано в коде ниже. Обратите внимание, что при использовании 2,002 против 2,001 десятичных цифр в setprecision расчет ввода может не потребоваться, но я использовал по крайней мере одну дополнительную цифру в качестве "защитной" цифры для любого потенциального округления.
setprecision(Int(ceil(log2(10) * 2002))) do
pi_str = string(BigFloat(pi))[1:3+1999]
digits_str = pi_str[3:3+1999]
println("Pi to 2,000 digits to right of decimal point is:")
println(pi_str[1:2])
for start in 1:50:1951
println(digits_str[start:start+49])
end
end
Я нахожу замечательным, что Юлия может решить эту проблему с таким небольшим количеством кода! Я также пробовал это для 10000 цифр после запятой, и это прекрасно работало.
Вот вывод:
julia> include("solution.jl")
Pi to 2,000 digits to right of decimal point is:
3.
14159265358979323846264338327950288419716939937510
58209749445923078164062862089986280348253421170679
82148086513282306647093844609550582231725359408128
48111745028410270193852110555964462294895493038196
44288109756659334461284756482337867831652712019091
45648566923460348610454326648213393607260249141273
72458700660631558817488152092096282925409171536436
78925903600113305305488204665213841469519415116094
33057270365759591953092186117381932611793105118548
07446237996274956735188575272489122793818301194912
98336733624406566430860213949463952247371907021798
60943702770539217176293176752384674818467669405132
00056812714526356082778577134275778960917363717872
14684409012249534301465495853710507922796892589235
42019956112129021960864034418159813629774771309960
51870721134999999837297804995105973173281609631859
50244594553469083026425223082533446850352619311881
71010003137838752886587533208381420617177669147303
59825349042875546873115956286388235378759375195778
18577805321712268066130019278766111959092164201989
38095257201065485863278865936153381827968230301952
03530185296899577362259941389124972177528347913151
55748572424541506959508295331168617278558890750983
81754637464939319255060400927701671139009848824012
85836160356370766010471018194295559619894676783744
94482553797747268471040475346462080466842590694912
93313677028989152104752162056966024058038150193511
25338243003558764024749647326391419927260426992279
67823547816360093417216412199245863150302861829745
55706749838505494588586926995690927210797509302955
32116534498720275596023648066549911988183479775356
63698074265425278625518184175746728909777727938000
81647060016145249192173217214772350141441973568548
16136115735255213347574184946843852332390739414333
45477624168625189835694855620992192221842725502542
56887671790494601653466804988627232791786085784383
82796797668145410095388378636095068006422512520511
73929848960841284886269456042419652850222106611863
06744278622039194945047123713786960956364371917287
46776465757396241389086583264599581339047802759009
Вот краткий код для распечатки Пи. Он находится в файле с именем "pi_print.jl" и содержит фактический АЛГОРИТМ для вычисления цифр числа Пи с использованием bigint.
function main()
firsttime_flag = true
counter = 2000
(k, a, b, a1, b1) = (BigInt(2), BigInt(4), BigInt(1), BigInt(12), BigInt(4))
while counter > 0
(p, q, k) = (k*k, BigInt(2)*k+BigInt(1), k+BigInt(1))
(a, b, a1, b1) = (a1, b1, p*a+q*a1, p*b+q*b1)
(d,d1) = ( div(a,b),div(a1,b1) )
while d == d1 && counter > 0
if firsttime_flag
firsttime_flag = false
println("Pi to 2,000 digits to the right of decimal point is:")
write(stdout,string(d))
println(".")
else
write(stdout,string(d))
counter = counter - 1
end
(a,a1) = ( BigInt(10) * (a % b), BigInt(10) * (a1 % b1) )
(d,d1) = ( div(a,b),div(a1,b1) )
end
end
end
main()
Вот вывод (который я усек)
$ julia pi_print.jl
Pi to 2,000 digits to the right of decimal point is:
3.
1415926535897932384626433832795028841971693993751058209749445923078164
0628620899862141592653589793238462643383279502884197169399375105820974
...
используя REPL
$ julia
_
_ _ _(_)_ | Documentation: https://docs.julialang.org
(_) | (_) (_) |
_ _ _| |_ __ _ | Type "?" for help, "]?" for Pkg help.
| | | | | | |/ _` | |
| | |_| | | | (_| | | Version 1.0.3 (2018-12-18)
_/ |\__'_|_|_|\__'_| | Official https://julialang.org/ release
|__/ |
julia> include("pi_print.jl")
Pi to 2,000 digits to the right of decimal point is:
3.
1415926535897932384626433832795028841971693993751058209749445923078164062862
0899862803482534211706798214808651328230664709384460955058223172535940812848
1117450284102701938521105559644622948954930381964428810975665933446128475648
2337867831652712019091456485669234603486104543266482133936072602491412737245
8700660631558817488152092096282925409171536436789259036001133053054882046652
1384146951941511609433057270365759591953092186117381932611793105118548074462
3799627495673518857527248912279381830119491298336733624406566430860213949463
9522473719070217986094370277053921717629317675238467481846766940513200056812
7145263560827785771342757789609173637178721468440901224953430146549585371050
7922796892589235420199561121290219608640344181598136297747713099605187072113
4999999837297804995105973173281609631859502445945534690830264252230825334468
5035261931188171010003137838752886587533208381420617177669147303598253490428
7554687311595628638823537875937519577818577805321712268066130019278766111959
0921642019893809525720106548586327886593615338182796823030195203530185296899
5773622599413891249721775283479131515574857242454150695950829533116861727855
8890750983817546374649393192550604009277016711390098488240128583616035637076
6010471018194295559619894676783744944825537977472684710404753464620804668425
9069491293313677028989152104752162056966024058038150193511253382430035587640
2474964732639141992726042699227967823547816360093417216412199245863150302861
8297455570674983850549458858692699569092721079750930295532116534498720275596
0236480665499119881834797753566369807426542527862551818417574672890977772793
8000816470600161452491921732172147723501414419735685481613611573525521334757
4184946843852332390739414333454776241686251898356948556209921922218427255025
4256887671790494601653466804988627232791786085784383827967976681454100953883
7863609506800642251252051173929848960841284886269456042419652850222106611863
0674427862203919494504712371378696095636437191728746776465757396241389086583
264599581339047802759009
Следующий код вычисляет число Пи, используя формулу Рамануджана, также называемую рядом Рамануджана-Сато (см. статью в Википедии о ряде Рамануджана-Сато ), формула которой задается формулой
и сравнивает результат с собственной реализацией числа pi в Julia:
function compute_pi_ramanujan_formula(digits::BigFloat)
# Constants in the formula
A = BigFloat(2)*sqrt(BigFloat(2))/BigFloat(9801)
B = BigFloat(1103)
C = BigFloat(26390)
Ck = BigFloat(0)
D1 = BigFloat(1)
D2 = BigFloat(1)
Fk = BigFloat(1)
# Initialize variables
sum_term = B
total_sum = A*sum_term
k = BigFloat(0)
lastPi=BigFloat(0)
while true
k += BigFloat(1)
Ck = Ck+C # 26390k = 26390(k-1)+26390
Fk = Fk*4k*(4k-1)*(4k-2)*(4k-3) # (4k)! = [(4(k-1))! = (4k-4)!] + 4k*(4k-1)*(4k-2)*(4k-3)
D1 = D1*BigFloat(396)^4 # (396)^(4k) = 396^(4(k-1)) 396^4
D2 = D2*k^4 # (k!)^4 = ((k-1)!)^4 k^4
sum_term = A * Fk * (B + Ck) / D1 / D2
total_sum += sum_term
newPi = 1/total_sum
diff = newPi - lastPi
lastPi = newPi
# Check if we've reached the desired precision
if abs(diff) < BigFloat(10)^(-digits-1)
return newPi, k
end
end
return newPi, k
end
digits = 30 # referring to digits after the dot, which is why 2 is added below
setprecision(Int(ceil(log2(10) * (digits+2)))) do
julia_pi = BigFloat(pi)
ramanujan_pi, iterations = compute_pi_ramanujan_formula(BigFloat(digits))
println("\npi up to ",string(digits)," digits, computed with Ramanujan algorithm:","\n",string(ramanujan_pi)[1:digits+2],"\n")
println("pi up to ",string(digits)," digits, native julia implementation", "\n",string(julia_pi)[1:digits+2],"\n")
println("The difference (RamanujanPi - juliaPi) is lower than required precision:","\n",ramanujan_pi-julia_pi,"\n")
println("Total iterations to reach this precision with Ramanujan algorithm:\n",Int(iterations))
println("Total number of digits divided by 8:\n",digits/8)
# this number should be roughly the same as the number of iterations because each iteration is supposed to add 8 correct digits, according to this stackexchange post: https://math.stackexchange.com/questions/908535/ramanujans-approximation-for-pi
end
(Возможно, можно было бы сделать его несколько более эффективным и вычислять только1/total_sumодин раз, если бы кто-то реализовал другой способ проверки количества вычисленных цифр, а затем, возможно, нужно было бы только умножить наAодин раз в конце, а не на каждой итерации.)
Как показано в этом посте stackexchange , на каждой итерации алгоритм Рамануджана добавляет еще 8 правильных цифр. Приведенный выше алгоритм также экспериментально подтверждает это, т.е.iterationsприблизительно равноdigits/8для заданного количества цифр.