Как нормализовать матричные столбцы в CUDA с максимальной производительностью?

Question

Как нормализовать матричные столбцы в CUDA с максимальной производительностью?

Как эффективно нормализовать матричные столбцы в CUDA?

Моя матрица хранится в столбце-мажоре, и типичный размер - 2000x200.

Операция может быть представлена в следующем коде Matlab.

A = rand(2000,200);

A = exp(A);
A = A./repmat(sum(A,1), [size(A,1) 1]);

Может ли это быть эффективно сделано с помощью Thrust, cuBLAS и / или cuNPP?

Быстрая реализация, включающая 4 ядра, показана ниже.

Интересно, можно ли это сделать в 1 или 2 ядрах для повышения производительности, особенно для шага суммирования столбцов, реализованного cublasDgemv().

#include <cuda.h>
#include <curand.h>
#include <cublas_v2.h>
#include <thrust/device_vector.h>
#include <thrust/device_ptr.h>
#include <thrust/transform.h>
#include <thrust/iterator/constant_iterator.h>
#include <math.h>

struct Exp
{
    __host__ __device__ void operator()(double& x)
    {
        x = exp(x);
    }
};

struct Inv
{
    __host__ __device__ void operator()(double& x)
    {
        x = (double) 1.0 / x;
    }
};

int main()
{
    cudaDeviceSetCacheConfig(cudaFuncCachePreferShared);
    cublasHandle_t hd;
    curandGenerator_t rng;
    cublasCreate(&hd);
    curandCreateGenerator(&rng, CURAND_RNG_PSEUDO_DEFAULT);

    const size_t m = 2000, n = 200;
    const double c1 = 1.0;
    const double c0 = 0.0;

    thrust::device_vector<double> A(m * n);
    thrust::device_vector<double> sum(1 * n);
    thrust::device_vector<double> one(m * n, 1.0);

    double* pA = thrust::raw_pointer_cast(&A[0]);
    double* pSum = thrust::raw_pointer_cast(&sum[0]);
    double* pOne = thrust::raw_pointer_cast(&one[0]);

    for (int i = 0; i < 100; i++)
    {
        curandGenerateUniformDouble(rng, pA, A.size());


        thrust::for_each(A.begin(), A.end(), Exp());

        cublasDgemv(hd, CUBLAS_OP_T, m, n,
                &c1, pA, m, pOne, 1, &c0, pSum, 1);

        thrust::for_each(sum.begin(), sum.end(), Inv());

        cublasDdgmm(hd, CUBLAS_SIDE_RIGHT, m, n, pA, m, pSum, 1, pA, m);
    }

    curandDestroyGenerator(rng);
    cublasDestroy(hd);

    return 0;
}

8

performance matrix cuda thrust cublas

Источник

user1957265 08 янв '13 в 08:35

3 ответа

Решение

Вы должны быть в состоянии слить первый for_each работа с cublasSgemv позвонить в один reduce_by_key вызов. Если вы определяете / переопределяете функторы как:

struct Accessor : public thrust::unary_function<int,int>
{
    int lda;
    __host__ __device__ Accessor(int _lda) : lda(_lda) {};
    __host__ __device__ int operator()(const int& idx)
    {
        return idx/lda;
    }
};

struct Exp : public thrust::unary_function<double,double>
{
    __host__ __device__ double operator()(const double& x)
    {
        return exp(x);
    }
};

struct Inv : public thrust::unary_function<double,double>
{
    __host__ __device__ double operator()(const double& x)
    {
        return double(1.0) / x;
    }
};

Затем вы можете рассчитать нормированный выход как

Accessor columns(m);
thrust::reduce_by_key(
        thrust::make_transform_iterator(thrust::make_counting_iterator(int(0)), columns),
        thrust::make_transform_iterator(thrust::make_counting_iterator(int(m*n)), columns),
        thrust::make_transform_iterator(A.begin(), Exp()),
        thrust::make_discard_iterator(),
        sum.begin());

thrust::for_each(sum.begin(), sum.end(), Inv());

cublasDdgmm(hd, CUBLAS_SIDE_RIGHT, m, n, pA, m, pSum, 1, pA, m);

[отказ от ответственности: весь код написан в браузере и не проверен, используйте на свой страх и риск]

Помимо уменьшения количества вызовов ядра, использование причудливых итераторов устраняет необходимость в большой единичной матрице, которая должна уменьшить объем памяти и общее количество транзакций памяти для выполнения операций суммирования и возведения в степень.

3

Источник

user681865 09 янв '13 в 03:43

Вы можете использовать ArrayFire следующим образом

array A = randu(2000, 2000);
A = exp(A);
A /= tile(sum(A, 0), A.dims(0), 1);

Вы могли бы сделать это и в толчке. Но если вы собираетесь работать с матрицами (в отличие от простых векторов), вам придется делать это в цикле for, который не будет столь эффективным.

ОТКАЗ ОТ ОТВЕТСТВЕННОСТИ Я разработчик в Accelereyes, работающий над arrayfire.

РЕДАКТИРОВАТЬ Я работаю над созданием новых ориентиров в соответствии с просьбой.

РЕДАКТИРОВАТЬ Мы нашли ошибки производительности для exp в нашем коде из-за этого теста. Мы рассматриваем и исправляем это.

2

Источник

user2192361 08 янв '13 в 23:24

Другие вопросы по тегам performance matrix cuda thrust cublas

user1957265 09 янв '13 в 08:41 2013-01-09 08:41 · Accepted Answer · 2013-01-09 08:41

Я сравнил производительность 3 подходов на M2090 с CUDA 5.0.

[173.179 us] реализация cublas, как показано в вопросе
[733.734 us] Чистая реализация Thrust с thrust::reduce_by_key от @talonmies
[1,508 мс] чистая реализация Thrust с thrust::inclusive_scan_by_key

$Performance on A_{2,000 x 200$

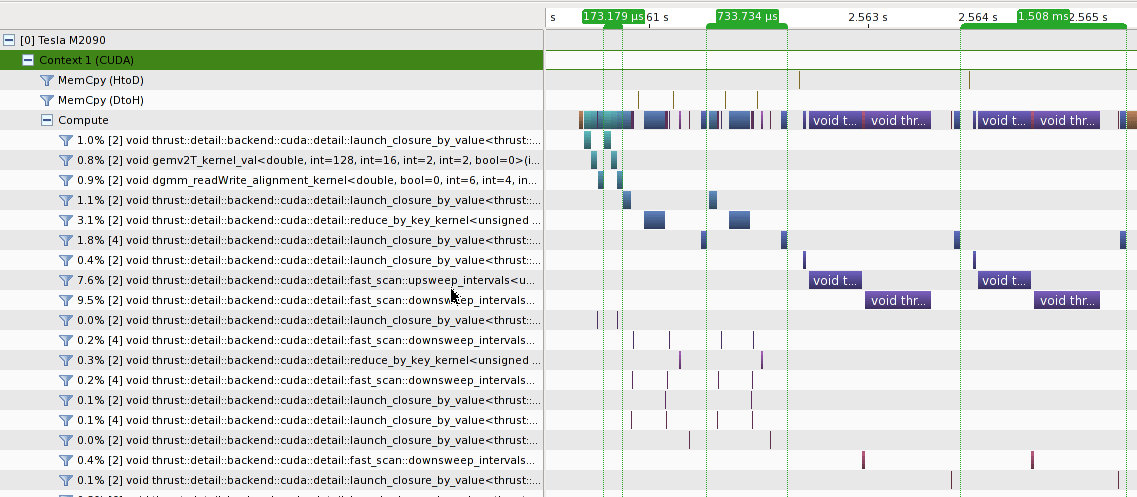
Видно, что

Cublas имеет самую высокую производительность в этом случае;
и то и другое thrust::reduce_by_key & thrust::inclusive_scan_by_key запускать несколько ядер, что приводит к дополнительным издержкам;
thrust::inclusive_scan_by_key записывает намного больше данных в DRAM по сравнению с thrust::reduce_by_key, что может быть одной из причин увеличения времени работы ядра;
Основное различие в производительности между кубами и упорным подходом заключается в суммировании столбцов матрицы. тяга медленнее, возможно, потому что thrust::reduce_by_key предназначен для сокращения отрезков с длиной варианта, но cublas_gemv() может применяться только к сегментам фиксированной длины (строка / столбец).

Когда матрица A достаточно велика, чтобы игнорировать издержки запуска ядра, подход cublas по-прежнему работает лучше всего. Результат профилирования на A_{20 000 x 2000} показан следующим образом.

$Performance on A_{20,000 x 2,000$

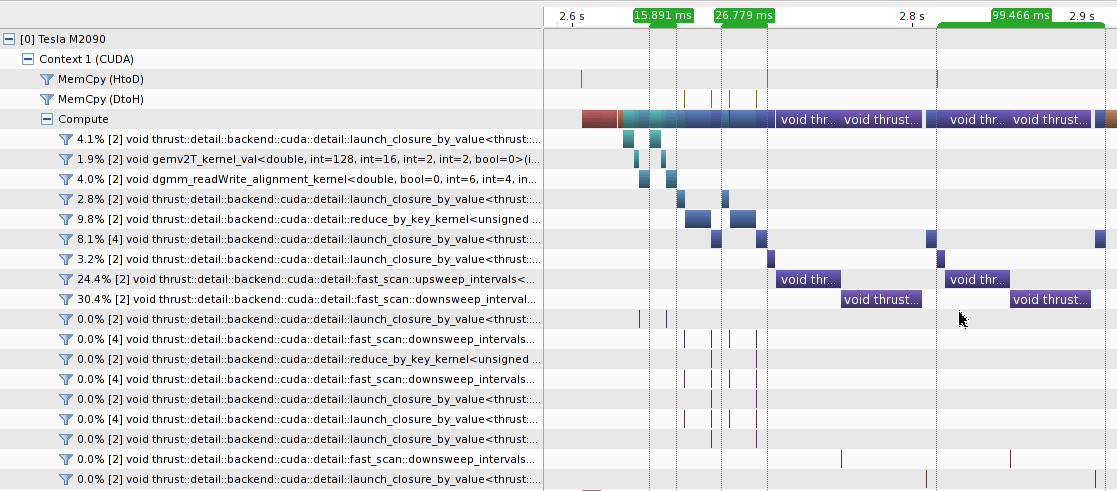
Фьюзинг первый for_each работа с cublasSgemv вызов как указано @talonmies может еще больше улучшить производительность, но я думаю, что ядро, написанное от руки, следует использовать вместо thrust::reduce_by_key,

Код для 3 подходов показан следующим образом.

#include <cuda.h>
#include <curand.h>
#include <cublas_v2.h>
#include <thrust/device_vector.h>
#include <thrust/device_ptr.h>
#include <thrust/transform.h>
#include <thrust/reduce.h>
#include <thrust/scan.h>
#include <thrust/iterator/counting_iterator.h>
#include <thrust/iterator/transform_iterator.h>
#include <thrust/iterator/discard_iterator.h>
#include <thrust/iterator/permutation_iterator.h>
#include <math.h>

struct Exp: public thrust::unary_function<double, double>
{
    __host__ __device__ double operator()(double x)
    {
        return exp(x);
    }
};

struct Inv: public thrust::unary_function<double, double>
{
    __host__ __device__ double operator()(double x)
    {
        return (double) 1.0 / x;
    }
};

template<typename T>
struct MulC: public thrust::unary_function<T, T>
{
    T C;
    __host__ __device__ MulC(T c) :
        C(c)
    {
    }
    __host__ __device__ T operator()(T x)
    {
        return x * C;
    }
};

template<typename T>
struct line2col: public thrust::unary_function<T, T>
{
    T C;
    __host__ __device__ line2col(T C) :
            C(C)
    {
    }

    __host__ __device__ T operator()(T i)
    {
        return i / C;
    }
};

int main()
{
    cudaDeviceSetCacheConfig(cudaFuncCachePreferShared);
    cublasHandle_t hd;
    curandGenerator_t rng;
    cublasCreate(&hd);
    curandCreateGenerator(&rng, CURAND_RNG_PSEUDO_DEFAULT);

    const size_t m = 2000, n = 200;
    const double c1 = 1.0;
    const double c0 = 0.0;

    thrust::device_vector<double> A(m * n);
    thrust::device_vector<double> B(m * n);
    thrust::device_vector<double> C(m * n);
    thrust::device_vector<double> sum1(1 * n);
    thrust::device_vector<double> sum2(1 * n);
    thrust::device_vector<double> one(m * n, 1);

    double* pA = thrust::raw_pointer_cast(&A[0]);
    double* pB = thrust::raw_pointer_cast(&B[0]);
    double* pSum1 = thrust::raw_pointer_cast(&sum1[0]);
    double* pSum2 = thrust::raw_pointer_cast(&sum2[0]);
    double* pOne = thrust::raw_pointer_cast(&one[0]);

    curandGenerateUniformDouble(rng, pA, A.size());

    const int count = 2;

    for (int i = 0; i < count; i++)
    {
        thrust::transform(A.begin(), A.end(), B.begin(), Exp());
        cublasDgemv(hd, CUBLAS_OP_T, m, n, &c1, pB, m, pOne, 1, &c0, pSum1, 1);
        thrust::transform(sum1.begin(), sum1.end(), sum1.begin(), Inv());
        cublasDdgmm(hd, CUBLAS_SIDE_RIGHT, m, n, pB, m, pSum2, 1, pB, m);
    }

    for (int i = 0; i < count; i++)
    {
        thrust::reduce_by_key(
                thrust::make_transform_iterator(thrust::make_counting_iterator(0), line2col<int>(m)),
                thrust::make_transform_iterator(thrust::make_counting_iterator(0), line2col<int>(m)) + A.size(),
                thrust::make_transform_iterator(A.begin(), Exp()),
                thrust::make_discard_iterator(),
                sum2.begin());
        thrust::transform(
                A.begin(), A.end(),
                thrust::make_permutation_iterator(
                        sum2.begin(),
                        thrust::make_transform_iterator(thrust::make_counting_iterator(0), line2col<int>(m))),
                C.begin(),
                thrust::divides<double>());
    }

    for (int i = 0; i < count; i++)
    {
        thrust::inclusive_scan_by_key(
                thrust::make_transform_iterator(thrust::make_counting_iterator(0), line2col<int>(m)),
                thrust::make_transform_iterator(thrust::make_counting_iterator(0), line2col<int>(m)) + A.size(),
                thrust::make_transform_iterator(A.begin(), Exp()),
                C.begin());
        thrust::copy(
                thrust::make_permutation_iterator(
                        C.begin() + m - 1,
                        thrust::make_transform_iterator(thrust::make_counting_iterator(0), MulC<int>(m))),
                thrust::make_permutation_iterator(
                        C.begin() + m - 1,
                        thrust::make_transform_iterator(thrust::make_counting_iterator(0), MulC<int>(m))) + n,
                sum2.begin());
        thrust::transform(
                A.begin(), A.end(),
                thrust::make_permutation_iterator(
                        sum2.begin(),
                        thrust::make_transform_iterator(thrust::make_counting_iterator(0), line2col<int>(m))),
                C.begin(),
                thrust::divides<double>());
    }

    curandDestroyGenerator(rng);
    cublasDestroy(hd);

    return 0;
}