Гео-поиск (расстояние) в PHP/MySQL (производительность)
У меня есть MySQL-таблица (MyISAM), содержащая около 200 тыс. Записей пар долг / долг, которые я выбираю, исходя из расстояния между парами (формула большого круга) из другой пары широта / длинна. (например, все записи, которые находятся в радиусе 10 км от 50.281852, 2.504883)
Моя проблема в том, что этот запрос занимает около 0,28 сек. запустить только для этих 200 000 записей (которые продолжают получать больше с каждым днем). Время 0,28 сек. было бы нормально, этот запрос выполняется очень часто, так как он обеспечивает основную функцию моего веб-приложения, и часто это часть большого запроса.
Есть ли способ ускорить это? Obviosly MySQL должен каждый раз проходить все 200 тыс. Записей и выполнять формулу большого круга для каждой записи. Я читал кое-что о гео-хешировании, R-деревьях и тому подобном здесь на stackru, но я не думаю, что это именно то, чего я хочу. Отчасти потому, что я никогда не был большим поклонником математики, но в основном потому, что я думаю, что эта проблема уже была решена кем-то умнее меня в библиотеке / расширении / и т.д. это было тщательно протестировано и регулярно обновляется.
MySQL, кажется, имеет пространственное расширение, но оно не обеспечивает функцию расстояния. Должен ли я смотреть на другую базу данных, чтобы поместить эти пары координат? PostgreSQL, похоже, имеет довольно зрелое пространственное расширение. Вы знаете что-нибудь об этом? Или PostgreSQL слишком просто использует формулу большого круга для получения всех записей в определенном регионе?
Может быть, есть специализированный отдельный продукт или расширение mysql, которое уже делает то, что я ищу?
Или, может быть, есть библиотека PHP, которую я мог бы использовать для расчетов? Используя APC, я мог легко поместить пары lat-long в память (эти 200-килобайтные записи занимают около 5 МБ), а затем выполнить запрос внутри PHP. Проблема с этим подходом заключается в том, что тогда у меня будет запрос MySQL, такой как SELECT .. FROM .. WHERE с идентификатором (id1, id2, ..) для всех результатов, который может достигать нескольких тысяч. Насколько хорошо MySQL обрабатывает подобные запросы? И потом (так как это задача обработки чисел) будет достаточно быстро делать это в PHP?
Любые другие идеи, что я должен / не должен делать?
Для полноты, вот пример запроса, лишенный каких-либо не относящихся к делу частей (как я уже говорил, обычно это часть большего запроса, в котором я объединяю несколько таблиц):
SELECT id, 6371 * acos( sin( radians( 52.4042924 ) ) * sin( radians( lat ) ) + cos( radians( 50.281852 ) ) * cos( radians( lat ) ) * cos( radians( 2.504883 ) - radians( lon ) ) ) AS dst
FROM geoloc
HAVING dst <10
ORDER BY dst ASC
Благодарю вас!
4 ответа
Вычислите ограничивающий прямоугольник, чтобы выбрать подмножество строк в предложении WHERE вашего SQL-запроса, чтобы вы выполняли только дорогостоящий расчет расстояния для этого подмножества строк, а не для всех записей 200 КБ в вашей таблице. Метод описан в этой статье на Movable Type (с примерами кода PHP). Затем вы можете включить расчет Haversine в ваш запрос по этому подмножеству, чтобы вычислить фактические расстояния, и учесть условие HAVING в этой точке.
Это ограничивающий прямоугольник, который помогает вашей производительности, потому что это означает, что вы выполняете дорогостоящий расчет расстояния только на небольшом подмножестве ваших данных. По сути, это тот же метод, который предложил Патрик, но ссылка "Подвижный тип" содержит подробные объяснения метода, а также PHP-код, который можно использовать для создания ограничивающего прямоугольника и вашего SQL-запроса.
РЕДАКТИРОВАТЬ
Если вы не думаете, что haversine является достаточно точным, то есть также формула Винсенти.
// Vincenty formula to calculate great circle distance between 2 locations expressed as Lat/Long in KM
function VincentyDistance($lat1,$lat2,$lon1,$lon2){
$a = 6378137 - 21 * sin($lat1);
$b = 6356752.3142;
$f = 1/298.257223563;
$p1_lat = $lat1/57.29577951;
$p2_lat = $lat2/57.29577951;
$p1_lon = $lon1/57.29577951;
$p2_lon = $lon2/57.29577951;
$L = $p2_lon - $p1_lon;
$U1 = atan((1-$f) * tan($p1_lat));
$U2 = atan((1-$f) * tan($p2_lat));
$sinU1 = sin($U1);
$cosU1 = cos($U1);
$sinU2 = sin($U2);
$cosU2 = cos($U2);
$lambda = $L;
$lambdaP = 2*M_PI;
$iterLimit = 20;
while(abs($lambda-$lambdaP) > 1e-12 && $iterLimit>0) {
$sinLambda = sin($lambda);
$cosLambda = cos($lambda);
$sinSigma = sqrt(($cosU2*$sinLambda) * ($cosU2*$sinLambda) + ($cosU1*$sinU2-$sinU1*$cosU2*$cosLambda) * ($cosU1*$sinU2-$sinU1*$cosU2*$cosLambda));
//if ($sinSigma==0){return 0;} // co-incident points
$cosSigma = $sinU1*$sinU2 + $cosU1*$cosU2*$cosLambda;
$sigma = atan2($sinSigma, $cosSigma);
$alpha = asin($cosU1 * $cosU2 * $sinLambda / $sinSigma);
$cosSqAlpha = cos($alpha) * cos($alpha);
$cos2SigmaM = $cosSigma - 2*$sinU1*$sinU2/$cosSqAlpha;
$C = $f/16*$cosSqAlpha*(4+$f*(4-3*$cosSqAlpha));
$lambdaP = $lambda;
$lambda = $L + (1-$C) * $f * sin($alpha) * ($sigma + $C*$sinSigma*($cos2SigmaM+$C*$cosSigma*(-1+2*$cos2SigmaM*$cos2SigmaM)));
}
$uSq = $cosSqAlpha*($a*$a-$b*$b)/($b*$b);
$A = 1 + $uSq/16384*(4096+$uSq*(-768+$uSq*(320-175*$uSq)));
$B = $uSq/1024 * (256+$uSq*(-128+$uSq*(74-47*$uSq)));
$deltaSigma = $B*$sinSigma*($cos2SigmaM+$B/4*($cosSigma*(-1+2*$cos2SigmaM*$cos2SigmaM)- $B/6*$cos2SigmaM*(-3+4*$sinSigma*$sinSigma)*(-3+4*$cos2SigmaM*$cos2SigmaM)));
$s = $b*$A*($sigma-$deltaSigma);
return $s/1000;
}
echo VincentyDistance($lat1,$lat2,$lon1,$lon2);
Что если вы подойдете к проблеме с другой стороны?
10 км по прямой это:
- на широте равна ~1'(минута)
- по долготе равна ~6'(минут)
Используя это в качестве основы, сделайте небольшую математику и добавьте в свой запрос WHERE предложение, удаляющее любые местоположения, которые находятся за пределами "коробки", которая создается путем добавления буферной зоны с допущением 1' lat & 6' long
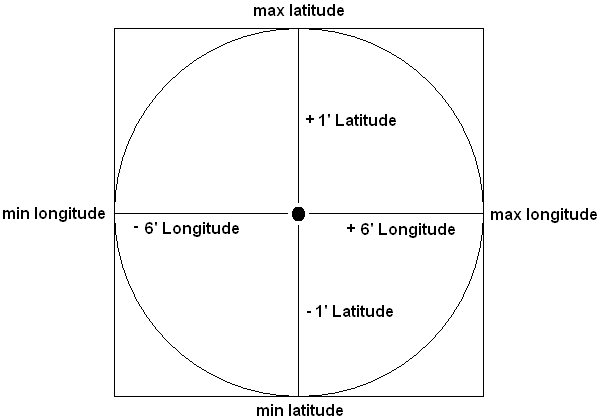
Работа с этим изображением:
- Местоположение GPS, которое вы ищете (34° 12' 34,0", -85° 1' 1,0") [34.2094444444, -85.0169444444]
Вы найдете минимальную / максимальную широту / долготу
2а. Мин. Широта - 34.1927777778, -85.0169444444
2b. Мин. Долгота - 34.2094444444, -85.1169444444
2с. Максимальная широта - 34.2261111111, -85.0169444444
2d. Макс. Долгота - 34.2094444444, -84.9169444444
Запустите ваш запрос с минимальным и максимальным значением для каждого направления
SELECT * FROM geoloc WHERE lat >= 34.1927777 AND lat <= 34.2261111 AND long >= -85.1169444 AND long <= -84.9169444;
Вы можете интегрировать вычисление расстояния с запросом SQL или использовать библиотеку / класс PHP для запуска проверки расстояния после извлечения данных. В любом случае вы сократили количество вычислений на большой процент.
Я использую следующую функцию для вычисления расстояния между двумя местоположениями GPS US84. Передаются два параметра, каждый из которых представляет собой массив, первый элемент которого представляет собой широту, а второй элемент - долготу. Я считаю, что он имеет точность в несколько футов, что должно быть достаточно для всех, кроме самых сложных основных GPS-офилов. Кроме того, я считаю, что здесь используется формула расстояния Хаверсайна.
$ distance = figureGPSDistance(массив (34.32343, -86.342343), массив (34.433223, -96.0032344));
function calculateGPSDistance($site1, $site2)
{
$distance = 0;
$earthMeanRadius = 2.0891 * pow(10, 7);
$deltaLatitude = deg2rad($site2[0] - $site1[0]);
$deltaLongitude = deg2rad($site2[1] - $site1[1]);
$a = sin($deltaLatitude / 2) * sin($deltaLatitude / 2) + cos(deg2rad($site1[0])) *
cos(deg2rad($site2[0])) * sin($deltaLongitude / 2) * sin($deltaLongitude / 2);
$c = 2 * atan2(sqrt($a), sqrt(1-$a));
$distance = $earthMeanRadius * $c;
return $distance;
}
ОБНОВИТЬ
Я забыл упомянуть, моя функция расстояния будет возвращать расстояние в футах.
Вы можете попробовать Quadkey. Это пространственный индекс и уменьшить размерность. Карта подразделяется на тайлы, но вы можете использовать ее для хранения очков. Вы можете скачать мой php класс hilbert-curve @ phpclasses.org. Он также включает в себя z-кривую и кривую Мура. Важно знать, что он использует проекцию Меркатора. Вы можете искать плитки карт Bing. Это объясняет, как использовать Quadkey. Вам нужны координаты x,y и значение z (увеличение или глубина). Тогда это дает вам Quadkey.
То, что я делал до сих пор, так же, как @Mark, описанный выше. Я полагаю, что это жизнеспособное решение для небольших сайтов, но не очень хорошее для моего случая (200 тыс. Записей, локализованных внутри блока размером 100х100 кв. Км, сосредоточенного вокруг заданной точки. Я использовал этот же трюк Марка, но производительность слишком низкая. 5 пользователей / второй запрос на ближайшие точки широты / долготы в течение нескольких часов, и запросы начинают занимать до 10 - 15 секунд, и это происходит после того, как я настроил настройки mySQL в my.cnf. Даже не хочу думать о том, что произойдет, когда там будет 2 миллиона записей по всему миру.
Итак, теперь время для шага 2: кривая Гильберта. Это должно решить проблему индекса B-дерева для столбцов (широта, долгота), которая является расточительной (при сканировании в диапазоне, используется только одна часть индекса B-дерева), используя только один индекс на один столбец (hilbert_number). hilbert_number - это число, рассчитываемое на основе координат широты / долготы точки на кривой Гильберта.
Но вторая проблема, связанная с проверкой расстояния между фиксированной точкой и всем от предыдущего подмножества результатов по формуле Хаверсайна, остается. Эта часть может быть очень медленной. Поэтому я подумал о том, чтобы как-то более непосредственно проверить расстояние, поместить все на кривую Гильберта и применить некоторую битовую маску к этому подмножеству результатов вместо применения формулы Хаверсайна. Я просто не знаю, как бы я поступил об этом...
В любом случае, другой прием, который я использовал, чтобы уменьшить количество точек в подмножестве результатов, заключался в том, чтобы использовать два ограничивающих прямоугольника и включать в подмножество только серые / белые точки для дальнейшего тестирования Haversine:

Сейчас мне нужно переключиться на числа Гильберта и посмотреть, как они себя ведут. Но я сомневаюсь, что это увеличит производительность в 10 раз!